Bonjour

À ton niveau, tu dois être facilement capable de démontrer que la force de freinage (force de Laplace ici) appliquée à chaque volume élémentaire d de conducteur en mouvement à la vitesse par rapport à la source de champ magnétique créant, au niveau du volume élémentaire, un champ magnétique de vecteur , a pour expression :



( : conductivité du conducteur en mouvement)

Reste ensuite à exprimer le moment élémentaire de cette force par rapport à l'axe de rotation puis à intégrer sur tout le volume du conducteur en mouvement soumis au champ magnétique.

La présence d'un double produit vectoriel peut faire un peu peur au départ mais en général, pour les dispositifs usuels, la situation s'arrange bien et on obtient un couple de freinage proportionnel à la vitesse angulaire du conducteur en rotation et au carré de la norme du vecteur champ magnétique.

Merci
Mais je veux Juste savoir dans le double produit vectorielle on a le champ magnétique appliqué au départ par l electroaimant ou le champ magnetique induit par courant de foucault et de plus j'ai pas encore compris comment calculer le champ magnétique suffisant en tesla pour freiner.

Ici, désigne le vecteur champ créé par l'électroaimant, pas celui induit par les courants de Foucault.
Ensuite, il te faut modéliser le frein. Il en existe plusieurs modèles. Le plus simple à mettre en équation : un disque de rayon R tournant à la vitesse angulaire par rapport à l'électroaimant qui crée un champ magnétique uniforme au niveau du disque de direction perpendiculaire au disque. Tu dois être capable d'expliciter le moment du couple de freinage en fonction de la conductivité , de R, de et de B.
Reste alors un problème de mécanique classique : quelle couple de freinage faut-il en fonction de la masse du train, de la décélération souhaitable ???
De plus, ce type de frein n'est pas le seul à agir...

bonjour
     j'ai tellement besoin de votre aide mes amis concernant mon tipe le freinage par courant de foucault j'ai beaucoup trompé dans la partie théorique de mon tipe. quelqu'un peut m'aider en calculons la force de la place et le moment pour une pièce conductrice cylindrique d'épaisseur e en rotation dans un champ magnétique .

merci beaucoup d'avance.

*** message déplacé ***

Oui alors mon probléme est est ce que je dois modéliser la pièce comme un disque d épaisseur négligeable ou un cylindre et le grand probléme pour moi c'est comment savoir le sens du courant de foucault car le signe - me gêne c est à dire le courant de foucault doit être dirigé vers la circonférence ou l inverse

Et merci beaucoup pour votre aide

Bonjour
Ce message fait un peu double emploi avec l'autre sur les courants de Foucault. Je vais te poster dans l'autre sujet un schéma qui devrait t'aider...

*** message déplacé ***

Merci beaucoup c'est parce que je doit présenter mon tipe le jeudi prochain

*** message déplacé ***

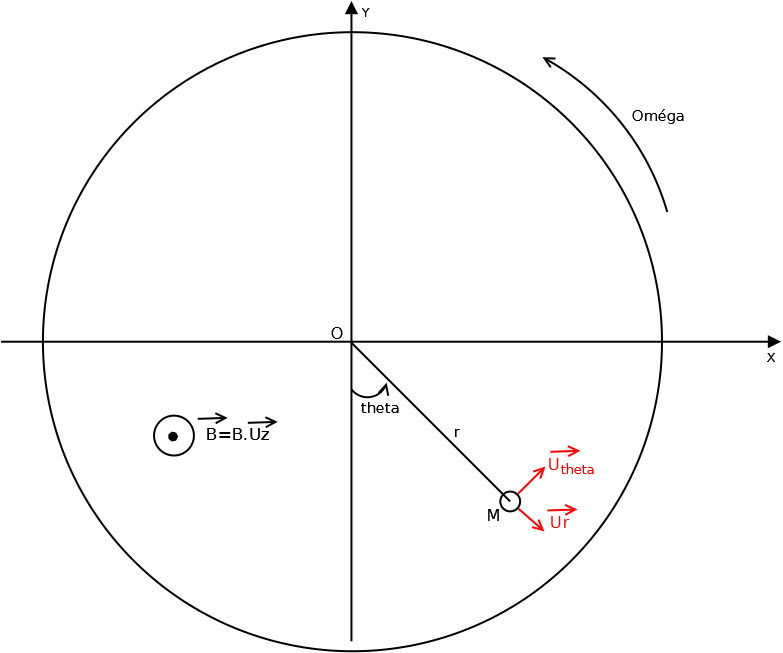
Je pars des formules que j'ai fournie dans mon message du 04-07-21 à 10:58. Si la démonstration te pose problème, demande de l'aide. Je considère donc un cylindre de rayon R, d'épaisseur « e » qui tourne à la vitesse angulaire instantanée autour de l'axe de symétrie (Oz). Soit un point M dans le plan de figure de coordonnées polaires (r, ) entourée d'un volume élémentaire :



Le champ magnétique est supposé uniforme en tout point du disque, de vecteur :



La vitesse du point M est :



Tu peux ainsi exprimer le vecteur force élémentaire. Tu peux ensuite calculer le moment élémentaire en O de cette force élémentaire :



Tu vas vérifier bien sûr que, conformément à la loi de Lenz, il s'agit d'un moment qui tend à freiner le disque... Reste pour finir, pour obtenir le moment en O, à intégrer l'expression sur tout le cylindre. Je te laisse continuer.

Merci beaucoup
J'ai encore deux petite probléme:

   1/v=OM (er) ^w(ez) =-Rw(e théta) mais je vois toujours qu'elle égale à Rw(ethéta) sans le moins

   2/est ce que je peux modéliser ce phénomène juste par un disque d épaisseur négligeable pour faciliter la tache ??
Je suis désolé pour le derangement

Il faut bien faire intervenir l'épaisseur afin de pouvoir définir un volume élémentaire d = e.dS. L'épaisseur « e » est suffisamment faible devant le rayon R du cylindre de sorte que le problème est invariant à l'intérieur du cylindre par translation suivant l'axe (Oz). Cela revient effectivement à assimiler le cylindre à un disque au niveau des calculs.

Regarde bien la figure et imagine que le disque tourne à la vitesse angulaire dans le sens positif défini sur la figure. On voit bien que le vecteur vitesse d'un point M quelconque du disque possède la direction et le sens du vecteur unitaire . Pour la formule vectorielle de la vitesse :

Bonsoir,

@ Zoro20 : merci de respecter les règles du forum :

extrait de la FAQ du forum :

Q03 - Pourquoi ne faut-il pas faire du ''multi-post'' ?

Pour de nombreuses raisons.

Pour mémoire, le multi-post consiste à reposer une même question dans un sujet différent , ou à poser des questions successives d'un même problème dans des sujets différents.

De même, une demande identique sur plusieurs sites sera considérée comme un multipost et la discussion pourra être fermée par un modérateur.

Etant donné tous les désagréments créés par le multi-post, le non-respect de cette règle entraînera votre exclusion temporaire ou définitive du forum !

Voici maintenant quelques raisons qui font que nous combattons avec autant d'ardeur le multi-post (et ses adeptes ) :

• La perte de temps pour les modérateurs qui consacrent leur temps bénévolement pour garantir la qualité des sujets et des échanges sur le forum.
  
• Le respect du travail des correcteurs qui consacrent leur temps bénévolement pour aider ceux qui sollicitent de l'aide.
  
• La lisibilité du forum de manière à ce qu'un sujet ayant déjà reçu de l'aide soit facilement identifié et qu'un sujet n'en ayant pas encore reçu puisse à son tour en recevoir.

Rappelez-vous une nouvelle fois la règle d'or du forum :
1 sujet créé = 1 problème

Zoro20, je fais mon TIPE sur le même sujet que toi, j'aurais peut être besoin de ton aide est ce que tu peux me contacter ici stp : ***adresse mail supprimée***

Bonjour,

@faonlime :

extrait de la FAQ du forum :

Q07 - Puis-je mettre mon adresse mail dans mon message afin d'inviter les visiteurs du forum à rentrer en contact avec moi ?

Non.

Tout d'abord, le principe du forum est de fournir de l'aide de manière publique : ainsi si vous obtenez une réponse sur le forum, la réponse donnée pourra éventuellement resservir plus tard pour un autre élève qui rencontre la même difficulté que vous.

De plus, lorsque vous postez votre mail sur un forum public comme celui-ci, il y a en effet de grandes chances qu'une personne malveillante (pirate informatique, fraudeur, etc.) ou qu'un logiciel conçu par ces derniers (robot, ...) finisse par récupérer celle-ci. Les modérateurs seront contraints de supprimer celle-ci.

Si vous souhaitez cependant être joignable par d'autres membres du site, tout en étant relativement protégé du spam, du phishing ou autre, il suffit de cocher la case " Afficher mon adresse email sur le forum " dans votre profil. Ainsi, les seuls membres, mais seulement les membres pourront visualiser votre mail en se rendant dans votre profil (il suffit de cliquer sur l'icône à côté de votre pseudo). De plus, l'affichage de cet email est même géré de façon à gêner sa récupération par d'éventuels robots spammeurs, sans pour autant gêner l'affichage pour les membres réels du site.