Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

force et statique

Posté par
hillel 06-03-24 à 11:34

bonjour, voila j'ai un exercice sur lequel je rencontre des difficultés :
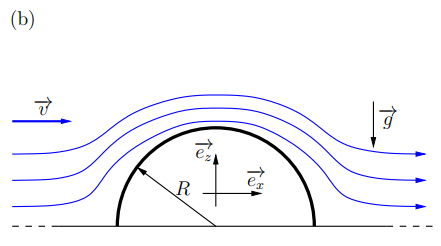
Une œuvre d'art contemporain, qu'on désignera par \mathcal{A}, se présente sous la forme d'une surface rigide de forme cylindrique de rayon R=15 \mathrm{~m}, de largeur L=4 \mathrm{~m} et de masse m=3000 \mathrm{~kg}, posé verticalement sur le sol comme sur la FIGURE 1. Le contact entre \mathcal{A} et le sol, qu'on supposera réduit à un point pour les calculs, suit la première loi du frottement de Coulomb, c'est à dire que \mathcal{A} ne glisse pas par rapport au sol tant que |\vec{T}| \leq \mu|\vec{N}|, où \vec{N} est la force de contact normale, \vec{T} la force de contact tangentielle, \mu=0.4 le coefficient de frottement et |$.$| signifie$ la norme d'un vecteur.
Soumis à un vent de travers de vitesse \vec{v}=v \overrightarrow{e_x} (avec v>0, cf. FigURE 1b), \mathcal{A} subit des forces aérodynamiques de portance \vec{F}_p=\frac{1}{2} C_z \rho S v^2 \vec{e}_z et de trainée \vec{F}_t=\frac{1}{2} C_x \rho S v^2 \overrightarrow{e_x}, où \rho=1 \mathrm{~kg} \mathrm{~m}^{-3} est la masse volumique de l'air, S=R L la section efficace et C_z=1.4 et C_x=1.2 sont les coefficients de portance et de trainée, respectivement.(a) ABSENCE DE VENT
On considère d'abord l'équilibre de \mathcal{A} en absence de vent.
i. Proposer un bilan des forces s'appliquant sur \mathcal{A}. Si \mathcal{A} est immobile, quelle équation satisfont ces forces? Donner les valeurs numériques des composantes de ces forces sur la base \left(\overrightarrow{e_x}, \overrightarrow{e_z}\right).
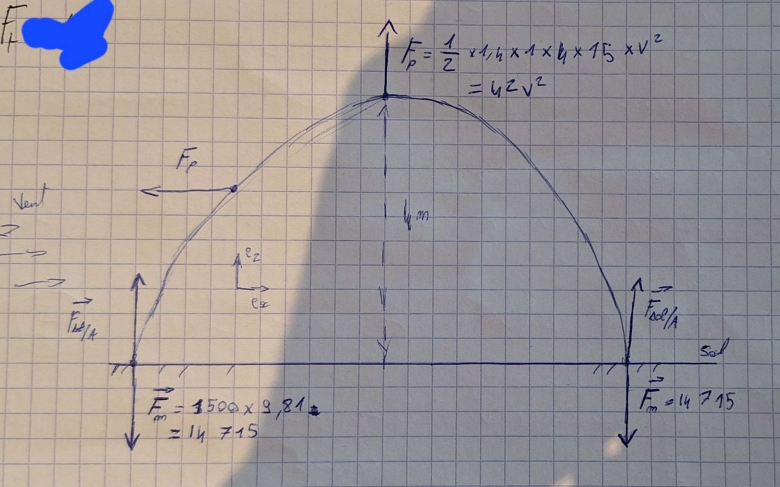
pour la A voila ce que j'ai fait mais je ne suis pas certains :

force et statique

Posté par
hillelre : force et statique 06-03-24 à 11:35

(juste voila le shema des bilans des forces que j'ai fait

Posté par
hillelre : force et statique 06-03-24 à 11:36

:

force et statique

Posté par
hillelre : force et statique 06-03-24 à 11:47

mon shema correspond plutot a la question (b) i) :
(b) PRESENCE DE VENT
Le vent souffle maintenant de travers à une vitesse \vec{v}=v \overrightarrow{e_x}, comme représenté sur la Figure 1(b). À la différence de la Figure 1(a), il n'y a pas de pierre sur les côtés de la sculpture \mathcal{A}.
i. Proposer un nouveau bilan des forces s'appliquant sur \mathcal{A} et faire un schéma correspondant.
ii. Établir que les forces de contact normale \vec{N}=N_z \overrightarrow{e_z} et tangentielle \vec{T}= T_x \overrightarrow{e_x} vérifient
\\ \left\{\begin{array}{l} \\ N_z=m g-\frac{1}{2} \rho R L C_z v^2 \\ \\ T_x=-\frac{1}{2} \rho R L C_x v^2 \\ \end{array}\right. \\
iii. En déduire les expressions littérales et les valeurs numériques ( \mathrm{en} \mathrm{km} \mathrm{h}^{-1} ) des deux vitesses limites de vent v_d et v_g au-delà desquelles \mathcal{A} décolle du sol ou glisse sur le sol, respectivement.
mais je pense que je vais redessiner mon shéma parce que je vois plusieurs erreurs...

Posté par
vanoisere : force et statique 06-03-24 à 12:16

Bonjour
Quelques remarques préliminaires.
L'énoncé fait référence à une figure fournie. Pourrais-tu la scanner et la poster ici ?
Le règlement du forum demande de copier la solution dans l'éditeur de texte plutôt que de scanner ce que tu as écrit...
Sinon : une règle très importante en dynamique. Pour un système étudié donné (ici le cylindre), les seules forces à prendre en compte son les forces extérieures, c'est à dire les forces exercées sur le système par le milieu extérieur. Si tu prends en compte à la fois les forces exercées par le milieu extérieur sur le système et les forces exercées par le système sur le milieu extérieur, le principe des actions réciproques conduit nécessairement à une résultante nulle.

Posté par
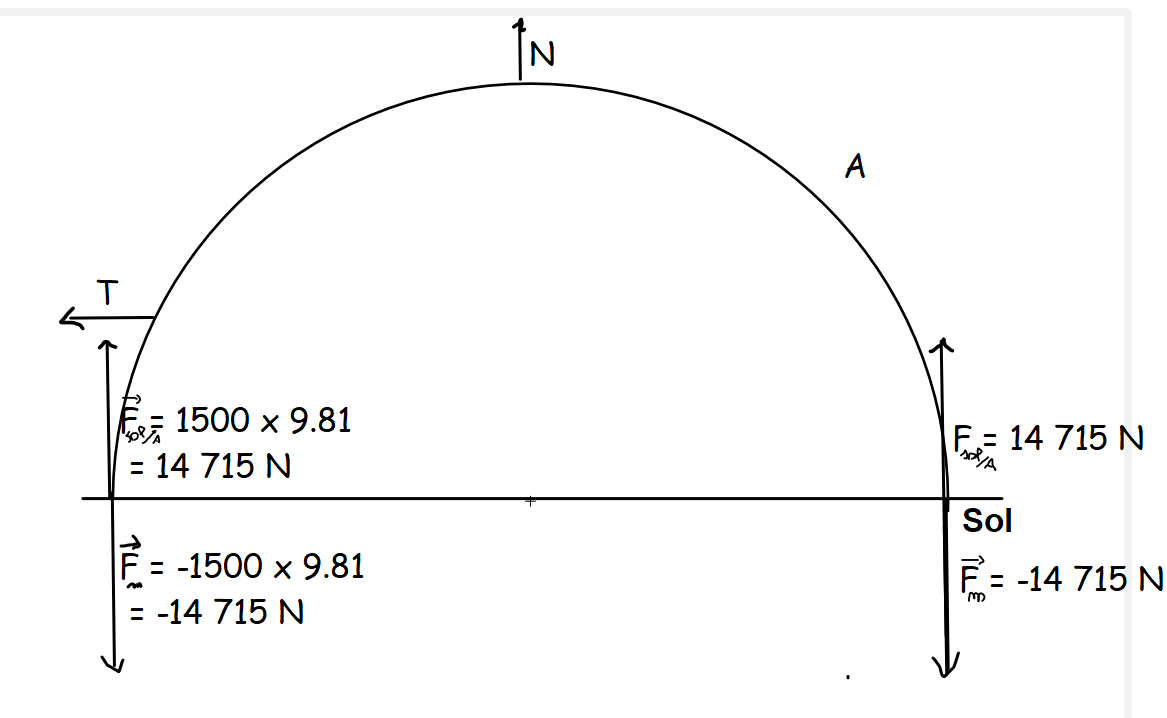
hillelre : force et statique 06-03-24 à 12:18

voila aussi un shéma que j'ai pensé pour la question (b) ii :
mais je suis pas sur de moi surtout que depuis ce shéma je ne vois pas comment trouver \\ \left{\begin{array}{l} \\ N_z=m g-\frac{1}{2} \rho R L C_z v^2 \ \\ T_x=-\frac{1}{2} \rho R L C_x v^2 \\ \end{array}\right. \\

force et statique

Posté par
hillelre : force et statique 06-03-24 à 12:21

Citation :

L'énoncé fait référence à une figure fournie. Pourrais-tu la scanner et la poster ici ?


force et statique

Posté par
hillelre : force et statique 06-03-24 à 12:24

Citation :
les seules forces à prendre en compte son les forces extérieures, c'est à dire les forces exercées sur le système par le milieu extérieur. Si tu prends en compte à la fois les forces exercées par le milieu extérieur sur le système et les forces exercées par le système sur le milieu extérieur, le principe des actions réciproques conduit nécessairement à une résultante nulle.

mais pour la question (a) i. il faut nécessairement que je prenne en compte les force réciproque de A si je veut que la somme des force soit nul et donc dire que A est immobile ?

Posté par
vanoisere : force et statique 06-03-24 à 12:30

Le poids et l'action du sol sont des actions extérieures...
Comme je l'ai expliqué dans mon premier message, ta façon de raisonner conduit nécessairement, compte tenu du principe des actions réciproques, à une résultante nulle, qu'il y ait équilibre ou pas !

Posté par
hillelre : force et statique 06-03-24 à 17:11

eu dans le cas de la question (a) je ne vois aucune force exterieure : il n'y a pas de vent.
les seuls forces que je vois c'est : le poids (qui se dessine sui les extrémités au sole de l'œuvre A) et les forces réciproques sinon je  vois pas

Posté par
vanoisere : force et statique 06-03-24 à 17:58

Je pense qu'il te faut vraiment revoir les bases...
1° : Le référentiel d'étude : ici la terre considéré comme référentiel galiléen :
2° : Le système étudié : le solide (A)
3° : les actions extérieures en absence de vent : (actions exercées sur (A) par le milieu extérieur) :
                 * le poids de vecteur \vec P=m\cdot\vec g (force d'attraction exercée par la terre)
                * la réaction du sol de vecteur \vec R
Le solide (A) étant en équilibre dans ce référentiel galiléen :

\overrightarrow{P}+\overrightarrow{R}=\overrightarrow{0}\quad;\quad\overrightarrow{R}=-m.\overrightarrow{g}=m.g.\overrightarrow{e_{z}}

Le poids est une force répartie dans tous le volume de la coque demie cylindrique (solide A) et la réaction du sol est une force répartie sur toute la surface de contact entre la coque et le sol horizontal mais l'énoncé demande de représenter les différentes forces à partir d'un même point. Cela est possible dans la mesure où ce problème n'envisage pas de rotation du solide (A). Ce point peut être l'origine du repère \left(O,\overrightarrow{e_{x}},\overrightarrow{e_{y}}\right)

Posté par
hillelre : force et statique 07-03-24 à 11:46

je vois mais dessiner toutes les forces en un point je vois pas trop vu que le contacte entre A et le sol se fait en 2 points alors j'ai dessiné comme ca mais bon après pour la question (a) il ont juste demandé le bilan des force j'ai pas besoin de schéma ?
et pour les valeurs numériques \vec P = -3000 * 9,81 = -29,4 * 10^3\vec e_z et donc \vec R = 3000 * 9,81 = 29,4 * 10^3\vec e_z

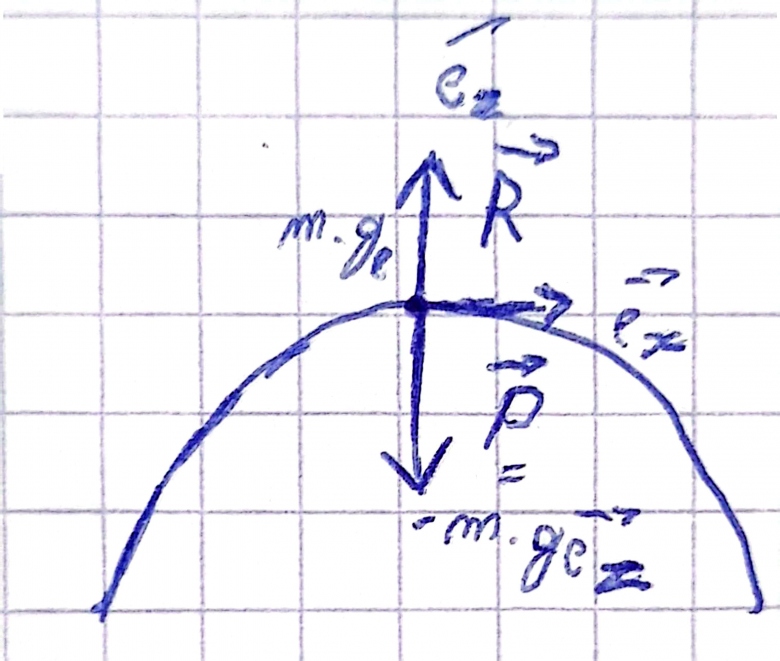
force et statique

Posté par
vanoisere : force et statique 07-03-24 à 14:22

Ok. Représenter les différentes forces extérieures à partir d'un même point permet d'obtenir simplement l'accélération du centre d'inertie du solide.

Posté par
hillelre : force et statique 08-03-24 à 14:30

je vois merci !!
est juste pour (2) si j'ai bien compris :
T est Ft sont deux forces opposées (qui devrait prendre la direction a peu près d une droite dérivé en un points de la courbe de A (je m exprime peut être un peu mal ) et le vecteur N devrait être la somme de Fp et R.
mais dans les calculs je recontre un probleme :
\vec N = 29,4 * 10^3 - 1/2 * 1 *4*15*1,2*v^2 = 29,358*10^3*v^2
\vec T = - 1/2 *15*1,2*v^2 = -36*v^2
et donc avec les valeurs absolues j'ai pour trouvé la vitesse minimum pour que A glisse :
-36v^2 \leq 29,358 * 10^3 * v^2
ce qui n'a aucun sens mais je ne vois pas mon erreur
(dsl si mon schéma est horrible j'ai essayé de faire ce que j'ai pu en faisant partir tout les vecteurs d'un même point (\vec N, \vec R, \vec F_p sont sensé partir du même points))

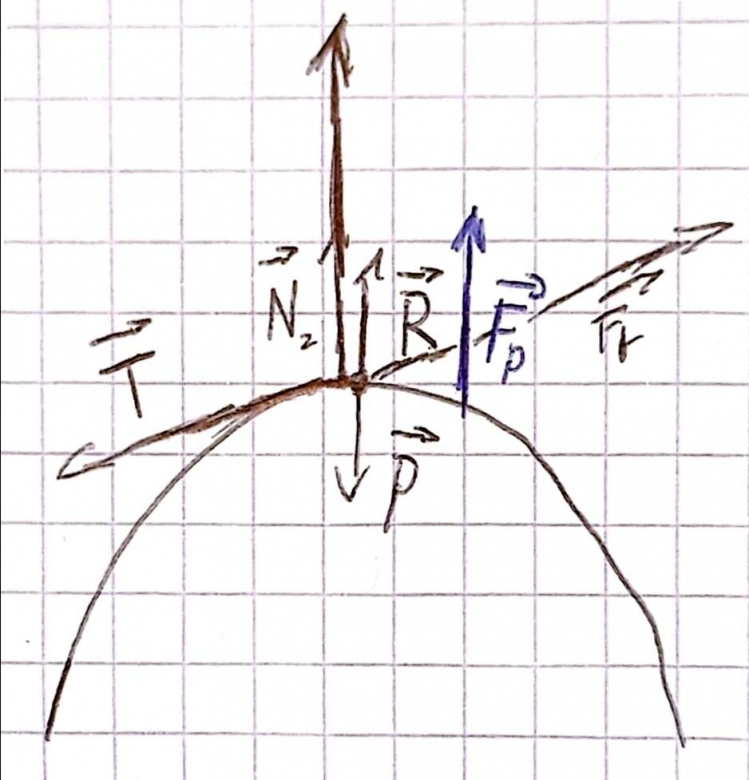
force et statique

Posté par
vanoisere : force et statique 08-03-24 à 15:45

A ce niveau, il faut raisonner littéralement puis faire les applications numériques demandées ensuite.
Je ne comprends pas tes difficultés à faire un schéma : tous les vecteurs forces appartiennent au même plan (O,\vec e_x,\vec e_z).
Il suffit d'écrire la relation fondamentale de la statique et d'en déduire les normes des vecteurs \vec T  et \vec N.
Ensuite :
le solide se met à glisser si :

\Vert\overrightarrow{T}\Vert>\mu.\Vert\overrightarrow{N}\Vert
Ensuite : la vitesse minimale du vent conduisant au décollage du solide est celle qui conduit à \Vert\overrightarrow{N}\Vert=0.

Posté par
vanoisere : force et statique 08-03-24 à 15:55

Le serveur gérant le forum fonctionne très mal en ce moment. Il est très lent et ne transmet pas toujours les schémas... Je retente ma chance ...

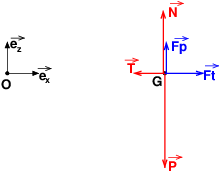
force et statique

Posté par
hillelre : force et statique 10-03-24 à 15:13

alors sur le shéma je vous suit mais pour ce qui est des calculs je suis un peu perdu :
du schéma je vois que \vec N = \vec F_p - \vec P = mg + \frac{1}{2} \rho R L C_z v^2 se qui ne va pas avec ce que je suis sensé trouvé dans l'énoncé du ii.
puis aussi dans les calculs :
\begin{aligned} \\ & \vec{N}=29 388 - 1 / 2 * 1 * 4 * 15 * 1,2 * v^2 = 29 352 * v^2 \\ \\ & \vec{T}=-1 / 2 * 15 * 1,2 * v^2 = -36 * v^2 \\ \end{aligned}
donc -36 v^2 \leq 29 352 * v^2 * 0,4  ->  0 \leq 11 740.4 * v^2 + 36 v^2 -> 0 \leq v  ca voudrait dire qu'au moindre vent A glisse ce qui est insensé
de même  \vec N = 0  ->  29 352 * v^2 = 0  ->  v = 0
ce qui est aussi insensé je comprend pas

Posté par
vanoisere : force et statique 10-03-24 à 15:56

Attention à ne pas confondre vecteur et norme d'un vecteur...

On suppose le solide en équilibre par rapport à la terre. La résultante de toutes les forces extérieures est le vecteur nul :

\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{T}+\overrightarrow{F_{p}}+\overrightarrow{F_{t}}=\overrightarrow{0}

On projette sur l'axe vertical :

\Vert\overrightarrow{N}\Vert+\Vert\overrightarrow{F_{p}}\Vert-\Vert\overrightarrow{P}\Vert=0 donc : \Vert\overrightarrow{N}\Vert=\Vert\overrightarrow{P}\Vert-\Vert\overrightarrow{F_{p}}\Vert

\Vert\overrightarrow{N}\Vert=m.g-\frac{1}{2}\rho.C_{z}.S.v^{2}

On projette sur l'axe horizontal :

\Vert\overrightarrow{F_{t}}\Vert-\Vert\overrightarrow{T}\Vert=0 donc : \Vert\overrightarrow{T}\Vert=\Vert\overrightarrow{F_{t}}\Vert=\frac{1}{2}\rho.C_{x}.S.v^{2}

Pour que cet équilibre persiste, il faut aussi :

\Vert\overrightarrow{T}\Vert\leq\mu.\Vert\overrightarrow{N}\Vert

Soit :

\frac{1}{2}\rho.C_{x}.S.v^{2}\leq\mu.\left(m.g-\frac{1}{2}\rho.C_{z}.S.v^{2}\right) \\
Je te laisse simplifier et obtenir l'inégalité vérifiée par v. Le cas limite de l'égalité est la vitesse limite vg au-delà de laquelle le solide commence à glisser sur le sol.

Je te laisse réfléchir à tout cela et continuer...

Posté par
hillelre : force et statique 10-03-24 à 16:39

Citation :
\frac{1}{2} \rho \cdot C_x \cdot S \cdot v^2 \leq \mu \cdot\left(m \cdot g-\frac{1}{2} \rho \cdot C_z \cdot S \cdot v^2\right)

oui c'est ce que j'ai fait j'ai juste fait une erreur d'inattention
voila c'est ce que j'ai trouvé maintenant :
36 v^2 \leq   0,4* (3000*9,81 - \frac{1}{2} *1.4*4*15*v2)    ->   -11 772 \leq   -19.2v^2   ->  v \leq 24.7
mais ca me parait quand même bien peu 24.7 km/h pour déplacer un objet de 3 tonnes

Posté par
vanoisere : force et statique 10-03-24 à 16:47

Attention : l'unité internationale de vitesse est le mètre par seconde. Il faut ensuite convertir en kilomètre par heure.
Revérifie aussi ton calcul... Je n'obtiens pas cette valeur...

Posté par
hillelre : force et statique 10-03-24 à 17:18

oui effectivement j'avais fait une erreur d'inattention
je trouve donc : v \leq 14,9
donc v doit être inferieur a   (14,9/100)*60*60 = 537.5
ca me parait beaucoup 537.5km/h même si ca a l'aire réaliste et pour faire décoller Ducoup j'ai v = 26m/s
donc 952 km/h

Posté par
vanoisere : force et statique 10-03-24 à 19:09

Attention : une application numérique non accompagnée de son unité , lorsque celle-ci existe, est en général considérée comme fausse un jour d'examen ou de concours.
Toujours pas d'accord avec ton calcul. Comme déjà écrit : conduit tout le calcul littéralement pour ne faire l'application numérique qu'ensuite. En reprenant mon message précédent, le cas limite de l'égalité correspond à :

\frac{1}{2}\rho.C_{x}.S.v_{g}^{2}=\mu.\left(m.g-\frac{1}{2}\rho.C_{z}.S.v_{g}^{2}\right) \\ \\ v_{g}^{2}.\left(\frac{1}{2}\rho.C_{x}.S+\frac{1}{2}\rho.\mu.C_{z}.S\right)=\mu.m.g \\ \\ v_{g}=\sqrt{\frac{2\mu.m.g}{\rho.S.\left(C_{x}+\mu.C_{z}\right)}}

Le résultat de l'application numérique est exprimé en m/s. L'énoncé demande de le convertir en km/h.

Ensuite, tu te focalises sur la masse : trois tonnes, qui te paraît énorme. La situation est à relativiser compte tenu de la surface de prise au vent : 40m2 qui est très importante. N'oublie pas que le solide est une sorte de coquille vide peu épaisse donc de densité moyenne très faible par rapport à la prise au vent. Imagine par contraste un demi cylindre de mêmes dimensions rempli de béton. Sa masse serait de l'ordre de 4000tonnes, pas 3tonnes comme ici !

Posté par
hillelre : force et statique 10-03-24 à 22:15

c'est noté, oui j'aurais du faire comme ca
ducoup la j'ai  v_g = \sqrt(\frac{2*0.4*3000*90.81}{4*15*(1.2+1.4)}) =12.2m/s
ce qui vaut 442 km/h
et pour  v_d j'ai m.g - \frac{1}{2} \rho R L C_z v^2 = 0  ->  v  =  \sqrt{\frac{m.g}{\frac{1}{2} \rho R L C_z}} = 26.4m/s = 952 km/h

Posté par
vanoisere : force et statique 10-03-24 à 23:33

Pour la vitesse de décollage, le calcul conduit à :
vd=26,47100840m/s qu'il convient d'arrondir à 26,5m/s.
Pour la conversion en km/h : réfléchis un peu au réalisme de ton résultat :952km/h alors que l'on commence à parler d'ouragan à partir de 120km/h ! Ton erreur : 1km=1000m, pas 100m !
Pour la vitesse de glissement : tu as oublié le coefficient de frottement µ dans le calcul.

Posté par
hillelre : force et statique 11-03-24 à 12:20

Citation :
Pour la vitesse de glissement : tu as oublié le coefficient de frottement µ dans le calcul.

eu si j'ai bien mis la vitesse de fortement qui 0.4 d'ailleurs ca me donne 12.28 m/s et qui donc donne 44km/h
Citation :
Pour la conversion en km/h : réfléchis un peu au réalisme de ton résultat :952km/h alors que l'on commence à parler d'ouragan à partir de 120km/h ! Ton erreur : 1km=1000m, pas 100m !

oui je comprend même pas comment je peux faire des erreurs pareil
en tout cas merci bcp !!!!

Posté par
vanoisere : force et statique 11-03-24 à 13:14

Tu as pris en compte µ au numérateur mais pas au dénominateur où tu dois remplacer Cz par µ.Cz. Cela devrait te conduire à vg=53,7km/h.

Posté par
hillelre : force et statique 11-03-24 à 15:06

a oui

Posté par
hillelre : force et statique 11-03-24 à 21:03

juste par contre j'ai pas compris pourquoi il faut que N = 0 pour que A vole ?

Posté par
vanoisere : force et statique 11-03-24 à 21:12

\vec N représente la force exercée par le sol sur le solide. Si le solide décolle, cette force cesse d'exister.

Posté par
Moudjosre : force et statique 12-03-24 à 18:12

Bsr à tous.
Svp, qui pourrait me faire un condensé clair de cet exercice posté par @hillel?
J'arrive pas à le comprendre entièrement.
Merci

Posté par
vanoisere : force et statique 12-03-24 à 18:29

Bonjour Moudjos
Ce forum n'est pas un distributeur automatique de solutions...
Si tu commençais par poser des questions précises sur ce que tu n'as pas compris ?


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !