bonjour,

le lien entre force et énergie est la notion de travail, qui est une forme d'énergie apparaissant dans le 1er principe de la thermodynamique.
Toutefois une force peut très bien s'exercer sur un corps et avoir un travail nul.
C'est le cas notamment si une force est perpendiculaire au déplacement du point d'application.

Ex: un satellite en orbite autour de la terre a une énergie (mécanique) constante (si son altitude est suffisante pour éviter les frottements avec l'atmosphère) et pourtant il est soumis à la force gravitationnelle.

Merci Krinn pour votre réponse
Concernant le cas du satellite, ne faut-il pas considérer que, du fait même qu'il est soumis à la force gravitationnelle terrestre, celui-ci exerce un effet de marée sur la Terre, certes minime mais pourtant bien réel ?
De ce fait, pour compenser l'énergie dépensée par les marées qu'il provoque, son énergie potentielle diminue constamment de telle sorte qu'il s'éloigne progressivement de la Terre (si son altitude est suffisante pour éviter les frottements avec l'atmosphère) exactement comme la Lune...

Correction : l'énergie potentielle du satellite augmente puisque, comme la Lune, il s'éloigne de la Terre, désolé...

Bonsoir Krinn, Bonsoir andretou
Je veux bien répondre concernant l'apparent paradoxe entre la dissipation d'énergie par effet de marée et l'augmentation de la distance terre satellite. Pour comprendre, il faut tenir compte de la conservation du moment cinétique du système terre - satellite. L'effet de marée diminue la composante du moment cinétique dues au rotations propres des deux astres. Il en résulte une augmentation du moment cinétique orbital qui se traduit par une augmentation de la distance terre satellite. On estime par exemple que le ralentissement du mouvement de rotation propre de la lune jusqu'à l'actuelle synchronisation (la lune présente toujours la même face à la terre) s'est traduite pas un doublement de la distance terre - lune donc par une diminution d'un facteur 2³=8 de l'effet de marée créé sur la terre par la lune.
Plus de précision à ce sujet et une démonstration partie V du document ci-dessous (pages 20 et suivantes) :

Merci Vanoise pour votre réponse et pour ce document clair et complet.
Mais que se passe-t-il dans le cas d'une planète qui ne tourne plus sur elle-même ?
Je suppose que, puisque son satellite même très lointain continue à produire des marées qui ont pour effet un échauffement (minime !) de la planète (donc un gain d'énergie pour la planète), il faut que de son côté le satellite perde de l'énergie potentielle en se rapprochant désormais de la planète jusqu'à épuisement total de son énergie potentielle...
Est-ce correct ?

Ta dernière interrogation correspond à la situation actuelle de la lune si on veut bien négliger l'effet de marée produit par le soleil et raisonner seulement sur le système {terre -soleil}
La terre exerce toujours un effet de marée sur la lune qui a pour effet de déformer légèrement la lune en forme d'ellipsoïde mais, comme la lune présente toujours la même face à la terre, cela ne dissipe plus d'énergie puisque cette déformation est fixe.
La lune exerce une force de marée sur la terre qui dissipe de l'énergie. La vitesse de rotation propre de la terre diminue très lentement, la distance terre-lune continue à augmenter très lentement. Cela s'arrêterait théoriquement lorsque la vitesse de rotation propre de la terre serait telle que la terre présente toujours la même face à la lune. Les effets de marée ne dissiperaient plus d'énergie. En absence d'autres phénomènes dissipateurs, la distance terre -lune resterait fixe.
Bien sûr : cela relève de la science-fiction : il faut tenir compte de l'influence du soleil et des faibles influences des autres planètes. De plus, la durée théorique pour atteindre une telle situation est supérieure à la durée de vie du soleil sous sa forme actuelle.

Si un jour la Terre présente toujours la même face à la Lune, on ne pourrait alors plus dire que la Lune tourne autour de la Terre, n'est-ce pas ?
De ce fait, l'énergie du système Terre-Lune ne varierait plus, mais la gravitation ne produirait plus aucune action puisque la Lune ne tournerait plus autour de la Terre.
Ma proposition "toute force extérieure à un système produisant une action (un effet) sur ce système fait nécessairement varier la quantité totale d'énergie contenue dans ce système" te paraît-elle correcte (au moins concernant la gravitation) ?

Attention à ne pas confondre mouvement orbital : le centre de la lune décrit dans un référentiel géocentrique un mouvement sensiblement elliptique (je dis sensiblement car il faut tenir compte en réalité de l'influence du soleil et des autres planètes) et rotations propres : la lune tourne autour de l'axe de ses pôles, la terre tourne autour de l'axe de ses pôles.
L'absence de dissipation d'énergie par effet de  marée créé par la terre sur la lune et par la lune sur la terre supposerait que la lune présente toujours la même face à la terre (c'est le cas maintenant) mais aussi que la terre présente toujours la même face à la lune. Là on en est loin : il faudrait que la terre tourne autour de l'axe de ses pôles dans un repère barycentrique à raison d'un tour par mois environ au lieu d'un tour par jour.
Attention : cela n'empêcherait pas la lune de tourner autour de la terre...Supprimer les effets dissipatifs des marées ne signifie pas supprimer les forces gravitationnelles.
As-tu bien compris les causes des effets de marée? J'explique cela assez simplement sur le document que je t'ai fourni.
Autre chose à bien comprendre : la cause de la dissipation d'énergie par effet de marée n'est pas l'existence de l'effet de marée mais le fait que la terre ne présente pas toujours la même face à la lune. Si la terre présentait toujours la même face à la lune, Il y aurait "marée haute" en permanence sur certaines côtes, "marée basse " en permanence sur d'autres côtes. Les marées ne produiraient plus de déplacement de matière et ne dissiperaient plus d'énergie.

Encore merci Vanoise pour tes explications. L'étude de l'interaction entre une planète et son satellite est diablement complexe. Et encore, tu t'es limitée au cadre de la mécanique newtonienne !...
En définitive, pourrais-tu STP rappeler dans quel(s) cas de figure une planète et son satellite n'échangent plus aucune énergie (en supposant que nous sommes en présence d'un système isolé) ?
Je crois avoir compris que c'est le cas lorsque la vitesse angulaire du satellite est égale à la vitesse de rotation de la planète (et que sa trajectoire est dans le plan de l'équateur). Est-ce correct ? Existe-t-il d'autres cas de figures ?

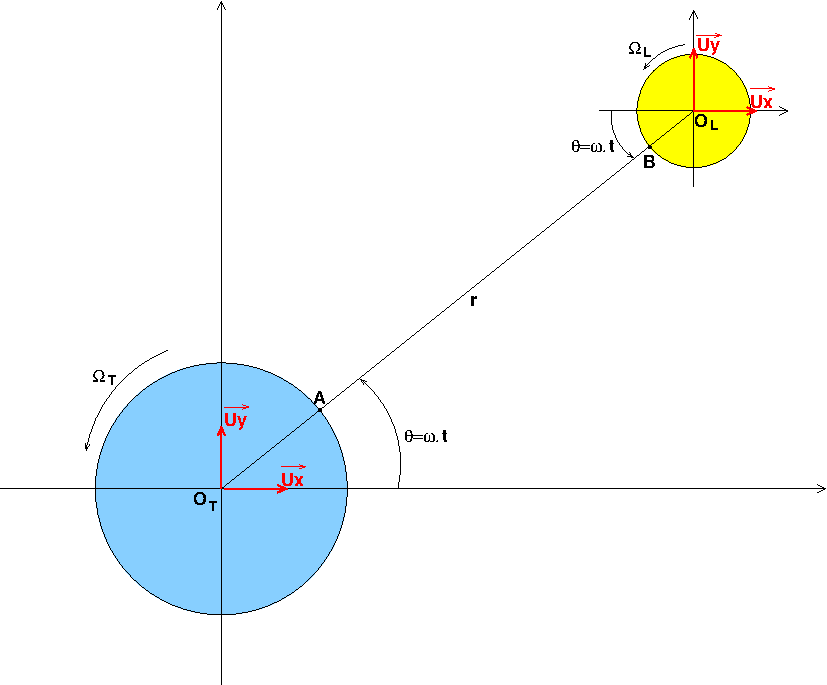
Un schéma aidera à comprendre. Dans le référentiel barycentrique (O_T, Ux,Uy), le centre O_L, est animé d'un mouvement circulaire uniforme de rayon r, à la vitesse angulaire, correspondant à une période d'un mois sidéral.
Pour que les effets de marée ne dissipe aucune énergie il faut, comme déjà dit, que la terre présente toujours la même face à la lune et que la lune présente toujours la même face à la terre.
En toute rigueur, cela suppose que l'axe des pôles terrestre et l'axe des pôles lunaire soient tous deux perpendiculaires au plan de figure (O_T, Ux,Uy). Le centre O_L de la lune devrait se déplacer dans le plan équatorial de la terre.
Cela suppose aussi que les deux vitesses  angulaires de rotation autour des axes des pôles, vitesses mesurées dans le repère barycentrique, soit égales à :
_T = _L =
Ainsi, par exemple, les points A et B resteraient toujours sur l'axe O_TO_L et ces points correspondraient toujours à des marées hautes.

Encore un grand merci Vanoise.
Encore 1 question : peut-on affirmer que seul un satellite géostationnaire n'échange aucune énergie avec la Terre (si on considère qu'ils forment un système isolé) contrairement aux satellites non-géostationnaires (qui produisent nécessairement un effet de marée) ?

Toujours en négligeant l'influence des autres astres, tu as raison d'affirmer qu'un satellite  de la terre ne produit pas de dissipation d'énergie par effet de marée sur la terre puisque, avec les notation de mon schéma : = _T dans ce cas.
Cependant, il peut y avoir dissipation d'énergie par effet de marée exercé par la terre sur le satellite si celui-ci ne tourne pas sur lui-même de façon à présenter toujours sa même face à la terre. Il faudrait avoir aussi : _L=.

Merci Vanoise.
Si je comprends bien, pour n'échanger aucune énergie avec la Terre, le satellite géostationnaire ne doit pas tourner sur lui-même. Car sinon la Terre produirait sur le satellite un effet de marée qui ralentirait sa rotation et dans ce cas, pour conserver le moment cinétique du système, le satellite s'éloignerait de la Terre et produirait à son tour un effet de marée sur la Terre, d'où un nouveau motif d'échange d'énergie et d'éloignement...
Mais dans l'absolu, l'orbite géostationnaire existe-t-elle réellement ? Car tout satellite, quelque soit sa taille, ne peut s'en rapprocher qu'avec un certain degré de précision (quand bien même la Terre serait parfaitement ronde et homogène). En supposant ainsi qu'un satellite (ne tournant pas sur lui-même) soit "parfaitement" sur l'orbite géostationnaire, sa période de rotation autour de la Terre ne sera jamais parfaitement égale à la période de rotation de la Terre, c'est une question de degré de précision de la mesure (à laquelle s'ajoute peut-être aussi l'imprécision de la constante G). De ce fait il persisterait un minuscule effet de marée qu'il est impossible d'annuler complètement.
Dans cette perspective, tant que la Terre est animée d'un mouvement de rotation sur elle-même, l'échange d'énergie entre la Terre et tout satellite ne serait pas égal à 0, cet échange tendrait seulement vers 0 dans le cas d'un satellite géostationnaire ne tournant pas sur lui-même...
Ce raisonnement est-il correct ?
Pardon d'abuser ainsi de votre patience...

Pardon, je voulais dire "synchroniser parfaitement les rotations..."

La perfection n'existe pas ! surtout pas en physique !