Inscription / Connexion Nouveau Sujet
force de frottement
j'ai un problème qui peut s'avere facil mais je parviens pas à le résoudre
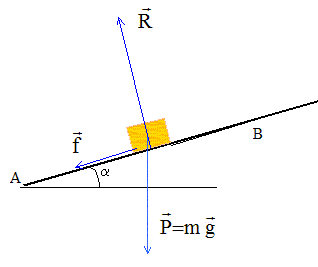
Un objet de masse m est lancé, dans le champ de pesanteur terrestre uniforme, avec une vitesse initiale
vers le haut, selon la ligne de plus grande pente d'un plan incliné faisant un angle
avec l'horizontale ;
le contact de l'objet avec le plan incliné est supposé avec frottement solide de coefficients
l'angle est inférieur à l'angle d'inclinaison maximal du plan pour lequel l'objet peut rester à l'équilibre qui est donné par
.
donner la vitesse minimale qui permet à l'objet de se mettre en mouvement
j'ai un problème qui peut s'avère facile mais je parviens pas à le résoudre
Un objet de masse m est lancé, dans le champ de pesanteur terrestre
le contact de l'objet avec le plan incliné est supposé avec frottement solide de coefficients
l'angle
donner la vitesse minimale

Bonjour
Cet énoncé n'est pas clair :
donner la vitesse minimale
S'il existe une vitesse, aussi faible soit-elle, il y a mouvement... ???
Salut vanoise.
Merci pour votre interaction.
Le corps initialement en repos.
Pour que le corps se mettre en mouvement vers le haut on doit par exemple appliquer une force F supérieur à (si je ne trompe pas)
si F <F0 le corps reste immobile
la question est ce qu'on a le meme analyse si on remplace la force F par la vitesse initiale, s'il y a une vitesse seuil V0 min si V <V0 le corps reste immobile
Ta dernière phrase semble indiquer que tu n'as pas parfaitement compris les relations de cause à effet en dynamique alors que la première partie de ton message est tout à fait correcte.
Partant d'un état d'équilibre d'un solide, si on modifie les forces qui sont appliquées à ce solide, on crée en général une accélération. La vitesse est toujours une fonction continue du temps. L'existence d'une accélération va donc se traduire par une variation de vitesse à partir de la valeur initiale qui, ici, est nulle.
Cette variation de vitesse au cours du temps peut être éventuellement rapide, lors d'un choc par exemple, mais ce que j'ai souligné au dessus reste cependant vrai.
Dans mon précédent message, j'ai répondu à ta question sur la vitesse sans avoir vérifié ta formule. Il y faut permuter le sinus et le cosinus.
Les force de frottement ont me causer toujours des difficultés
Je reviens après à la continuité de vitesse
Votre 1er message est très significatif. Il y a une vitesse, nécessairement il y a un déplacement dans l'espace par rapport au temps et par suite un mouvement.
Maintenant je vais poser le problème d'une autre façon pour présenter les difficultés que je rencontre.
Cela fait beaucoup d'hypothèses à faire
Supposons que le corps se déplace sur un trajectoire rectiligne qui se compose de deux parties :
-partie sans frottement
- partie avec frottement
Les deux parties sont continues en un point X0
On suppose que le corps S est en mouvement dans la partie sans frottement avec une vitesse (constante par exemple) est arrive au point X0
Est ce que le corps S continue son mouvement dans la partie avec frottement quoique la vitesse , ou il y a certains vitesse dans laquel le corps arrive en X0 est s'arrête.
Une autre proposition :
Supposons que le corps s se trouve en X0 immobile, il reçoit une vitesse par choc par exemple
Est ce que tous les valeurs de que va le corps reçoit permet un mouvement dans la partie avec frottement ou non
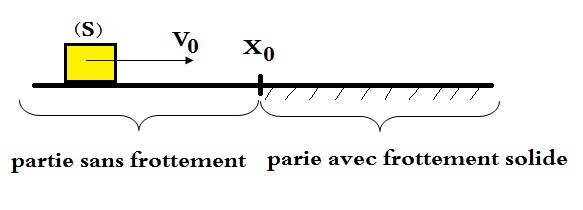
Supposont qu'à une date to, le centre d'inertie G du solide soit en Mo d'abscisse xo avec une vitesse Vo. Peu importe la façon dont cette vitesse a été acquise dans le contexte de ta question.
Pour x>xo, l'existence de frottement impose à G une accélération dans le sens opposé à celui de de sorte que le mouvement de G devienne retardé (freiné si tu préfères). La vitesse de G va donc diminuer au court du déplacement jusqu'à une immobilisation du solide. La longueur du parcours avant immobilisation est évidemment d'autant plus grande que Vo est une valeur importante et que le coefficient de frottement est faible. Bref : l'apparition des frottement crée une discontinuité en fonction du temps de l'accélération mais en aucun cas une discontinuité de vitesse.
Bonsoir Vanoise;
Merci pour votre explication.
J'ai encore mal compris la continuité de vitesse dans le temps
Est ce que ça veut dire que :
Explication physique :
la valeur de vitesse ne fait pas un brusque chute (c à d dans le même instant ) d'une valeur
par exemple à une autre valeur( 0 par exemple), mais passe par tous les valeurs qui se trouve entre
et 0, même dans un certain court temps
Explication mathématique :
la dérivé de vitesse en n'est pas infini
Chaque coordonnée du vecteur vitesse est une fonction continue du temps, au sens mathématique du terme. Revois ton cours de mathématique au besoin.
Concernant ta dernière remarque, tu sais que la dérivée par rapport au temps de la vitesse est l'accélération. Effectivement une accélération infinie supposerait une force infinie ; impossible !
Bonsoir Vanoise;
Merci pour l'explication
J'ai un problème que j'espère transposer correctement:
Revenons au corps S dans le plan incliné avec frottement solide.
si on applique une force F sur le corps vers le haut, le corps reste immobile tant que le force F ne dépasse pas la valeur à
à t=0, Le corps immobile, la somme des forces = 0
avec :
Ce que je ne comprends pas que :
Appliquer une force F de module compris entre 0 et à deux conséquences :
-Soit déséquilibrer la somme des forces et le rendre différent de 0 et par suite créer une accélération qui nécessite la création d'un mouvement, ce qui est n'est pas le cas, car le corps reste immobile
-Soit modifier le module de la force de frottement pour maintenir la somme des forces égales à 0 et par suite l'équilibre de corps S ce qui est n'est pas le cas, car les forces sont constant.
Dans les deux cas il y a une incompatibilité.
Revois au besoin ton cours sur la loi de Coulomb qui concerne les frottements solides.
En statique :
f µs.R
µs.R
où µs désigne le coefficient de frottement statique, légèrement supérieur au coefficient de frottement dynamique µ que tu utilises. Tu peux, pour une première approche considérer :
µs µ.
µ.
Ce qui est important ici pour répondre à ta question, c'est le remplacement d'une égalité par une inégalité.
![]()
Bonsoir Vanoise;
Bien comprendre; merci beaucoup.
J'ai une dernière question dans les forces de frottement.
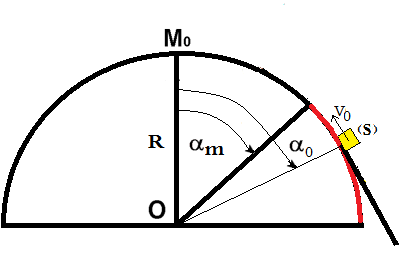
Si on un trajectoire circulaire, (exemple : une bille qui glisse sur un sphère)
Est ce que la formule
.
reste valable pour déterminer l'angle maximal
tel que pour tout la bille reste immobile (en équilibre)
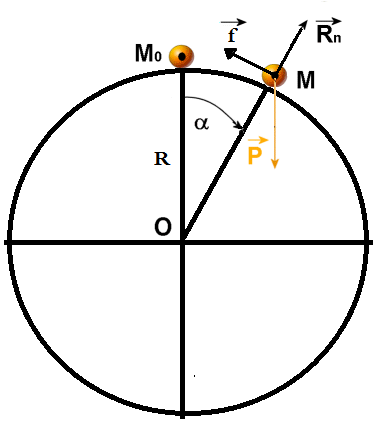
Je pense que non;
l'angle qu plan incliné et tout à fait différent à l'angle parcourus par un mobile dans un trajectoire circulaire
Mais dans ce cas, comment calculer l'angle  dont lequel la bille reste immobile
dont lequel la bille reste immobile
Le plan tangent en M à la trajectoire circulaire est incliné de quel angle par rapport à l'horizontale ?
Bonsoir Vanoise;
une autre question dans ce problème s'il vous plaît.
Dans la trajectoire circulaire, on suppose que la bille se trouve en
on applique une force F constante tangente à la trajectoire
on veut déterminer la force minimale qui met la bille en mouvement tel que pour F>
on a un mouvement et pour F<
la bille reste immobile à cause de frottement (par analogie au plan incliné
)
mois je procéde comme suit :
on doit déterminer V:
on utilse le theorème de l'energie cinetique:
avec : et
on suppose que
donc
Finalement je trouve une formule qui contient V et l'intégral de
ça veut dire l'intégrale de V
donc pour déterminer f on doit déterminer V qui nécessite la détermination de f
une boucle infini
donc comment remédier à ce problème.
Merci
Attention au réalisme : en présence de frottements, une petite bille, aussi petite soit-elle, va rouler plutôt que glisser, ce qui complique la mise en équation. Imagine plutôt un très petit cube qui glisse. En cas de glissement, la projection de la RFD dans le repère de Frénet conduit à :
En éliminant Rn entre ces deux équations, on obtient une équation différentielle non linéaire vérifiée par  . Aucune solution littérale. Il faut la résoudre numériquement avec un logiciel scientifique.
. Aucune solution littérale. Il faut la résoudre numériquement avec un logiciel scientifique.
Attention : ces équations ne sont valide que dans la mesure où Rn 0 : au-delà, le solide quitte la piste circulaire.
0 : au-delà, le solide quitte la piste circulaire.
Merci Vanoise;
j'ai deux questions:
1- pour determiner :
on a
est ce qu'on peut majorer cette expression ?
ça veut dire :
tel que pour tout on a un mouvement (comme le plan incliné)
2- est ce qu'on peut déterminer l'angle ou quitte le corps (S) la surface circulaire,
ça bien sur correspond à , mais on ne peut pas déterminer explicitement R_N. on retombe à nouveau dans l'équation différentielle d'ordre 2 non linéaire.
Puisque :
le contact persiste tant que :
En absence de frottement, le théorème de l'énergie cinétique permet facilement d'exprimer en fonction de
, ce qui permet de calculer
 m mais la situation se complique en présence de frottement car la force de frottement n'est pas constante et son travail ne peut pas s'exprimer simplement. Il faut recourir au calcul numérique à l'aide de logiciels spécialisés ou à l'aide d'un tableur.
m mais la situation se complique en présence de frottement car la force de frottement n'est pas constante et son travail ne peut pas s'exprimer simplement. Il faut recourir au calcul numérique à l'aide de logiciels spécialisés ou à l'aide d'un tableur.
Salut Vanoise.
Je m'excuse, j'ai une autre question dans ce sujet.
Dans la trajectoire circulaire, en absence de frottement, le corps (S) perd contact lorsque
Or
Théorème de l'énergie cinétique a nous donne l'expression de V en remplace dans R_N un calcul classique nous donne :
-sans vitesse initial :
implique
donc
-avec vitesse initial
et
donne
et nécessairement on a
Conclure : lorsque augmente
augmente et par suite
diminue (car cos(x) et décroissante entre 0 et
) jusqu'à
lorsque
Ma question :
Dans les deux cas la valeur maximale de et 48°
Est-ce que par analogie si la vitesse est inférieure (par frottement) à ces valeurs dans le cas normal ou il n'y a pas de frottement on trouve
Bonsoir ;
ce que je veux savoir, c'est la possibilité de l'existence d'un mouvement dans la partie rouge. C'est à dire entre la position et
avec
l'angle maximale ou le corps (S) quitte le le trajet circulaire s'il part de
s'il existe des condition de mouvement (frottement, vitesse,..) qui permet un mouvement entre et
si on pose le corps (s) par exemple à la position 80° est ce qu'il poursuite son mouvement sur la trajectoire circulaire (dans certain condition) ou quitte le trajet dés le départ
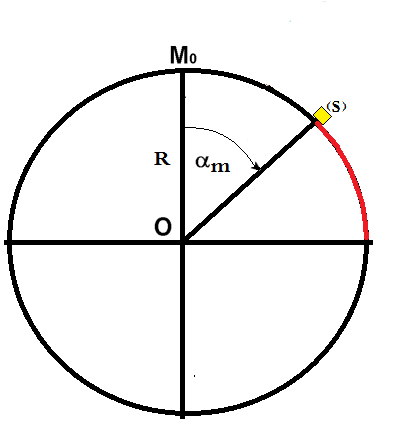
D'accord avec ton étude de la situation en absence de frottement. A noter que le cas Vo=0 est impossible physiquement car la position Mo est une position d'équilibre même s'il s'agit d'un équilibre instable.
A noter que pour Vo2> g.R le solide n'est jamais en contact avec la piste circulaire et décrit une trajectoire parabolique. En absence de frottement, pour une vitesse initiale inférieure à  (g.R), la valeur de
(g.R), la valeur de  telle que le mobile quitte la piste est effectivement inférieure à 48° .
telle que le mobile quitte la piste est effectivement inférieure à 48° .
Supposons maintenant la présence de frottement solide, le solide quittera toujours la piste pour V2=g.R.cos( ) mais, pour une même valeur de Vo, une même valeur de
) mais, pour une même valeur de Vo, une même valeur de  donc un même travail du poids, la vitesse sera plus faible. Donc, en présence de frottement, pour une même valeur de Vo, le mobile quittera la piste pour une position plus basse (valeur de
donc un même travail du poids, la vitesse sera plus faible. Donc, en présence de frottement, pour une même valeur de Vo, le mobile quittera la piste pour une position plus basse (valeur de  plus grande). On pourrait imaginer des valeurs de Vo et de µ telles que cette position corresponde à
plus grande). On pourrait imaginer des valeurs de Vo et de µ telles que cette position corresponde à  de très peu inférieur à 90°.
de très peu inférieur à 90°.
Bonsoir Vanoise, merci pour l'explication
Les choses maintenant est un peu clair, mais j'ai encore des difficultés à contourner tout le problème
Je pose le problème d'une autre façon :
Si on inverse le sens de mouvement vers le haut
Lorsque le corps (s) dans le 1er point de contact avec le trajet circulaire (je suppose dans un 1 er temps que les frottements sont négligeables)
on étude la possibilité de mouvement : il faut
condition sur la vitesse :
implique que
-est ce qu'il y a une condition sur l'angle pour que le corps poursuivre le mouvement sans quitter le trajet dès le départ
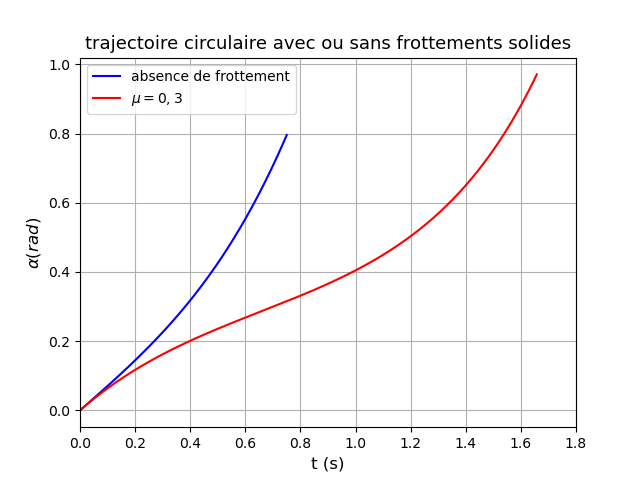
Juste une simulation informatique pour illustrer mon message du 03-11-23 à 22:19. Avec R=2,00m, Vo=1,4m/s j'ai représenté les courbes  =f(t) avec et sans frottement en arrêtant la simulation lorsque le mobile quitte la piste circulaire.
=f(t) avec et sans frottement en arrêtant la simulation lorsque le mobile quitte la piste circulaire.
En absence de frottement, le mobile quitte la piste à la date t=0,750s pour une valeur de  < 48° : 45,6° soit 0,80rad.
< 48° : 45,6° soit 0,80rad.
En présence de frottement (µ=0,3) le mobile reste plus longtemps sur la piste (1,66s) et quitte celle-ci pour une valeur de  >48° : 0,97rad soit 55,6°.
>48° : 0,97rad soit 55,6°.
Concernant ton dernier message : quel que soit le sens du mouvement, frottement ou pas, le mobile reste sur la piste circulaire tant que l'inégalité suivante est vérifiée :
Bonsoir Vanoise,
Merci beaucoup pour l'explication.
je reste dans le sens de mouvement vers le haut
si je comprend bien:
condition de l'angle
on doit réaliser toujours :
si
on trouve :
ce qui est absurde
donc l'angle ne peut être jamais 90°
un angle inférieur un peu à 90° est possible mais la vitesse doit etre très faible et tant qu'on diminue on peut augmenter la vitesse initiale à condition que l'inégalité
doit être vérifié
une petite question: lorsque le mobile monte et atteint l'angle maximale est s'arrête, est ce qu'il descend et reprend de nouveau l trajet circulaire ou quitte ce trajet définitivement
Effectivement, le raisonnement ne s'applique pas au cas limite  o = 90°. Cette situation correspond simplement à un lancé vertical vers le haut, la piste circulaire est sans influence sur le mouvement.
o = 90°. Cette situation correspond simplement à un lancé vertical vers le haut, la piste circulaire est sans influence sur le mouvement.
Merci beaucoup Vanoise.
et pour la question
lorsque le mobile monte et atteint l'angle maximale est s'arrête, est ce qu'il descend et reprend de nouveau l trajet circulaire ou quitte ce trajet définitivement
Si le mobile se déplace vers le haut en restant en contact avec la piste circulaire, il redescendra en restant également en contact. En effet, pour une valeur de  donnée, la valeur de v change de signe mais conserve la même valeur absolue (conservation de l'énergie en absence de frottement). Or la condition de contact fait intervenir v2.
donnée, la valeur de v change de signe mais conserve la même valeur absolue (conservation de l'énergie en absence de frottement). Or la condition de contact fait intervenir v2.
Merci beaucoup Vanoise.
Je me mets a la phase de montée
angle initiale :
La vitesse maximale et tel que :
Donc le mobile atteint le pont le plus haut dans le trajet circulaire soit \alpha_m l'angle correspond à ce point
Th de l'énergie cinétique :
remplaçons par son expression
on trouve
1-est ce que ce traitement est correct?
2- est ce qu'on peut considérer que l'angle parcouru est petit pour linéariser les équations de mouvement
OK pour la première question.
Pour la deux : tu choisis une vitesse initiale importante, celle correspondant à la limite du décollage. Pas de linéarisation possible ; de toutes les façons, même pour une valeur de Vo faible, je ne vois pas trop l'intérêt d'une telle linéarisation pour ce dispositif.


