Bonjour,
Je suis étudiant en première année d'école d'ingénieur, j'ai un exercice sur les fonctions de transfert et équations différentielles. Pouvez-vous m'aider à résoudre ce problème.

javascript:void(0)


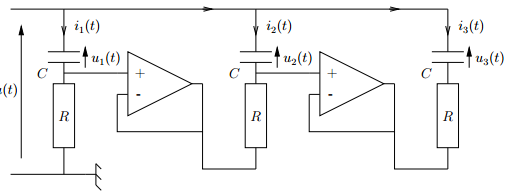
Le circuit électronique représenté ci-dessus. Les amplificateurs opérationnels sont supposés parfaits et ils fonctionnent en régime linéaire dans une configuration de suiveur. L'objectif est de commander les tensions  $ u_1,u_2,u_3$ aux bornes des condensateurs à l'aide de la tension de commande $ u$. Les trois condensateurs ont la même capacité $ C$ et sont déchargés à l'instant initial. Les trois résistances sont identiques et valent $ R$.

1- Analyse du système
On pose  $ \omega=\frac{1}{RC}$ et on prendra pour valeur numérique  $ \omega=1 rad/s$.

1.a) En utilisant les lois de Kirchhoff (loi des noeuds et mailles), déterminer les équations différentielles en  $ u_1,u_2,u_3$ qui régissent le fonctionnement du circuit.

1.b) Montrer que  $ x(t)=[u_1(t) \ u_2(t) \ u_3(t)]^{T}$ appartenant à l'ensemble des $ R^{3}$ est un vecteur d'état du système et déterminer l'équation d'état correspondante.
1.c) Quels sont les pôles du système en boucle ouverte ?
Lorsque la sortie mesurée par un capteur est  $ y(t)=u_3(t)$, on montre que la fonction de transfert du système est donnée par  $ G(p)=\frac{Y(p)}{U(p)}=\frac{\omega^{3}}{(p+\omega)^{3}}$.

Merci