Inscription / Connexion Nouveau Sujet
Fonction de transfert double intégrateur - AOP
Bonjour tout le monde,
L'électronique (principalement analogique) n'est pas trop mon fort, et là je coince sur un problème qui pourtant ne m'a pas l'air insurmontable :
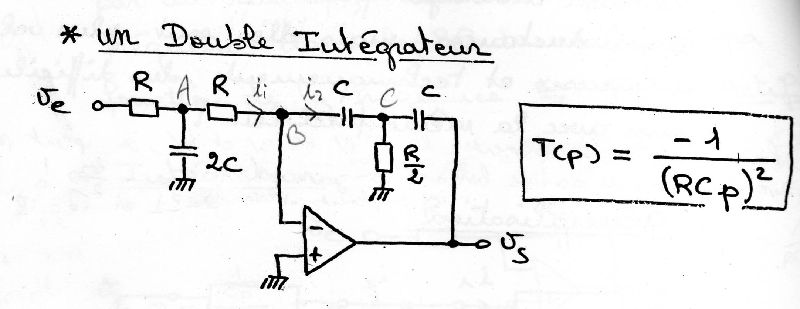
il s'agit de trouver la fonction de transfert T=vs/ve du montage ci-dessous. On sait qu'il s'agit d'un double intégrateur et donc on connait la réponse, donnée sur le schéma. Cependant, je n'arrive pas à retrouver le résultat !
Pour ce faire, on pourrait appliquer le théorème de Millmann au points A et C je pense, mais je n'ai pas encore exploré cette possibilité, car je souhaite tout d'abord passé par la loi d'Ohm complexe et les impédances.
On sait que e+ = e- = 0 et l'impédance d'entrée de l'ampli OP étant infinie, i1=i2. De là, on peut écrire ve=Z1*i1 et vs=-Z2*i2, donc i1=i2 donne ve/Z1=-vs/Z2, d'où on en tire T(p). Cependant, après avoir effectué ce calcul, je tombe sur une expression bien compliqué où je n'arrive pas à retrouver le résultat attendu !
Par exemple pour Z1, j'ai dit que c'était (2C) en parallèle avec R, le tout en série avec R ; et de même pour "l'autre côté".
Qu'est ce qu'il pourrait être faux ?
Quelqu'un peut m'éclairer ?
Merci beaucoup
J'ai essayé avec Millman au points A, B et C et ça marche, cependant quelqu'un pourrait me dire pourquoi ma première méthode n'aboutit pas ?
Merci
Voila sans Millmann :
Le potentiel de B est 0 volt (puisque V+ = V- et que V- = 0)
et donc vA/(R//2c) = Ve/(R + (R//2c))
R//2C = (R/(2pC))/(R + 1/(2pc)) = R/(1+2pRC)
vA/(R//2c) = Ve/(R + (R//2c))
vA.(1+2pRC)/R = Ve/(R + R/(1+2pRC))
vA.(1+2pRC)/R = Ve.(1+2pRC)/(2R+2pR²C)
vA = Ve.R/(2R+2pR²C)
vA = Ve/(2.(1+pRC))
i1 = i2 = vA/R
i2 = Ve/(R.(2+2pRC))
i2 = Ve/(2R.(1+pRC))
VC = - i2/(pC)
VC = -Ve/(2.pCR.(1+pRC))
i(R/2) = Vc/(R/2) = -Ve/(pCR².(1+pRC))
I(C tout à droite du schéma) = i2 - i(R/2)
I(C tout à droite du schéma) = Ve/(2R.(1+pRC)) + Ve/(pCR².(1+pRC))
I(C tout à droite du schéma) = Ve/(R.(1+pRC)) .(1/2 + 1/(pRC))
I(C tout à droite du schéma) = Ve/(R.(1+pRC)) .(2+pRC)/(2pRC)
I(C tout à droite du schéma) = Ve (2+pRC)/(2pR²C.(1+pRC))
Vs = Vc - (1/(pC)).I(C tout à droite du schéma)
Vs = -Ve/(2.pCR.(1+pRC)) - Ve.(2+pRC)/(2p²R²C².(1+pRC))
Vs = -Ve/(2.pCR.(1+pRC)) . [1 + (2+pRC)/(pRC)]
Vs = -Ve/(2.pCR.(1+pRC)) . [2(1+pRC)/(pRC)]
Vs = -Ve/(pCR) . [1/(pRC)]
Vs/Ve = -1/(pRC)²
-----

En fait j'ai pas pu attendre ce soir, donc je m'y suis mis. J'ai bien compris la méthode, les calculs, mais pourquoi ne peut-on pas "juste" faire vs/ve = -Z2/Z1 comme dit dans mon premier post,
avec Z1=R+(R//(2C)) et Z2=C+(C//(R/2)) ?
Le hic est que dans la relation Vs/Ve = - Z2/Z1
Z1 est l'mpédance entre l'entrée (Ve) et le V- de l'ampli... sans aucun "chemin" vers le masse.
Mais ici, le "2C" retourne vers la masse et donc on ne peut pas calculer ainsi l'impédance Z1
Pareil pour Z2, dans la relation Vs/Ve = - Z2/Z1, Z2 est l'impédance entre le V- de l'ampli et Vs ... sans aucun "chemin" vers le masse.
Mais ici, le "R/2" retourne vers la masse et donc on ne peut pas calculer ainsi l'impédance Z2.
Attention, je ne dis pas qu'il est impossible ici de calculer la fonction de transfert via un rapport d'impédances ... mais il faut alors le faire ici avec "circonspection" ... à cause du courant dérivé vers la masse aussi bien dans le circuit d'entrée que dans le circuit de réaction.




