Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... AutreForum autre de supérieur PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau autre
Partager :

Fonction de transfert & Bode

Posté par
Araii 02-05-18 à 15:35

Bonjour,
Je suis bloqué depuis quelques jours sur cet exercice, merci aux personnes pouvant répondre à mes questions

La fonction de transfert du circuit s'écrit :
T = Vs/Ve = (-j.R.C.)/(1+2.j.R.C.+(j.R.C.)2
La forme canonique de la fonction transfert est :
T = T0.(j(/0))/(1+j2m(/0+(j.(/0))2)
Montre que f0 = 1/(2*pi*R*C) ; T0 = -1 et m = 1

4. T peut se mettre sous la forme T= (T0.Q0)/(1+jQ0*((f/f0)-(f0/f)))
En déduire l'expression de Q0 en fonction de m et sa valeur numérique.

5. Le diagramme de Bode de ce circuit est donné en annexe.
Déterminer :
a. sa fréquence propre F0.
b. son facteur de qualité Q0.
c. Son facteur d'amortissement m.
d. La pente des asymptotes en dB/oct.
e. Mesurer les gain G0 à la fréquence f0. En déduire les valeurs de T0.

Fonction de transfert & Bode

Posté par
vanoisere : Fonction de transfert & Bode 02-05-18 à 16:05

Bonjour
Explique ce que tu as été capable de faire et ce qui te bloque. L'aide ultérieure sera plus efficace qu'un simple corrigé pas nécessairement adapté à ton niveau.

Posté par
Araiire : Fonction de transfert & Bode 02-05-18 à 16:21

Bonjour,
Ce qui me bloque c'est qu'en fait mon cours sur ce sujet n'a rien de similaire alors je ne sais pas par où attaquer. Et pour le diagramme de Bode c'est pareil, j'ai presque rien sur l'exploitation de ce dernier. J'ai chercher sur internet mais je n'ai rien trouver de vraiment convainquant...

Posté par
vanoisere : Fonction de transfert & Bode 02-05-18 à 16:36

Tu connais tout de même la relation entre fréquence et pulsation... Au départ, il suffit d'identifier terme à terme. Tu obtiens immédiatement :

RC\omega=\frac{\omega}{\omega_{0}}\quad donc\quad\omega_{0}=2\pi.f_{0}=\frac{1}{RC}

T_{0}=-1\quad;\quad m=1

Pour alléger les notations, je pose :

x=\frac{\omega}{\omega_{0}}=\frac{f}{f_{0}}

Ainsi, la fonction de transfert complexe s'écrit :

\underline{T}=T_{0}\cdot\frac{jx}{1+2m.jx+\left(jx\right)^{2}}

Pour obtenir l'expression demandée à la question 4), l'astuce consiste à diviser tous les termes par (j.x) puis à identifier.

Cette aide devrait te permettre de bien avancer. Je te laisse travailler...

Posté par
vanoisere : Fonction de transfert & Bode 02-05-18 à 16:46

Il semblerait que le serveur du site ne transmettent pas les formules. Voici l'image correspondante.

Fonction de transfert & Bode

Posté par
vanoisere : Fonction de transfert & Bode 02-05-18 à 16:46

La panne n'a été que de très courte durée...

Posté par
Araiire : Fonction de transfert & Bode 02-05-18 à 17:08

Merci pour votre réponse, mais j'ai plusieurs questions.
Comment je peux retrouver f0? Car l'expression la plus proche que j'ai trouvé en partant de votre aide est f0 = \frac{\omega_{0} \times RC}{2\pi}
Pourquoi \frac{\omega}{\omega_{0}} = \frac{f}{f_{0}} ?

Posté par
vanoisere : Fonction de transfert & Bode 02-05-18 à 17:24

2\pi.f_{0}=\frac{1}{RC}\quad donc\quad f_{0}=\frac{1}{2\pi.R.C}

Puisque, de façon générale, la pulsation s'obtient en multipliant la fréquence par 2\pi :

\frac{\omega}{\omega_{0}}=\frac{2\pi f}{2\pi f_{0}}=\frac{f}{f_{0}}

Tout cela est certainement dans ton cours et tu as sans doute traité de façon approfondie les filtres du premier ordre avant d'aborder le passe-bande comme celui-ci...

Posté par
Araiire : Fonction de transfert & Bode 02-05-18 à 17:29

D'accord merci bien !
J'ai eu beau chercher quand je suis tombé sur ce devoir j'ai rien trouver de vraiment similaire. Mon cours est assez mal fait mais peut-être que je n'ai pas bien chercher malgré tout ^^"
Je vais continuer un peu de mon coté et je reviens vers vous.
Merci beaucoup pour votre aide

Posté par
vanoisere : Fonction de transfert & Bode 02-05-18 à 17:43

Tu peux trouver assez facilement de l'aide sur le net :
ici par exemple (la lettre T est remplacée par H) :
ou ici à partir de la page 3 (mais tu peux aussi étudier le début ) :

Posté par
Araiire : Fonction de transfert & Bode 02-05-18 à 20:13

Je n'ai toujours pas réussi à exprimer Q0 en fonction de m, j'ai essayer en "bidouillant" la formule mais je ne trouve rien

Posté par
vanoisere : Fonction de transfert & Bode 02-05-18 à 22:07

Comme déjà expliqué, on peut diviser chaque terme par (jx) ; on peut aller un peu plus vite en divisant chaque terme par (2mjx) :

\underline{T}=T_{0}\cdot\frac{jx}{1+2m.jx+\left(jx\right)^{2}}=\frac{\frac{T_{0}}{2m}}{1+\frac{1}{2mjx}+\frac{jx}{2m}}

En posant : Q_{0}=\frac{1}{2m}=\frac{1}{2} :

T=\frac{T_{0}.Q_{0}}{1+jQ_{O}\cdot\left(x-\frac{1}{x}\right)}

Je te laisse continuer...

Posté par
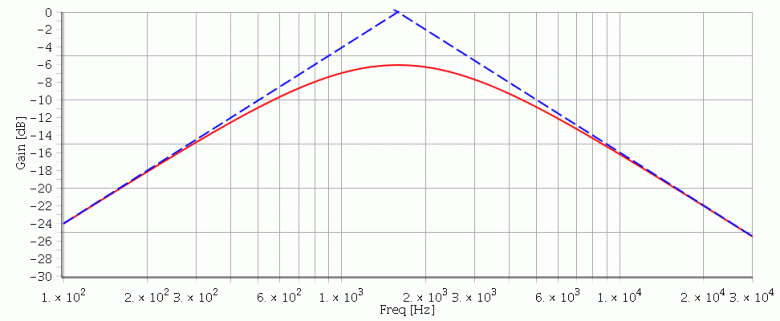
vanoisere : Fonction de transfert & Bode 03-05-18 à 15:02

Voici le diagramme de Bode avec les asymptotes à la courbe du gain (pointillés bleus). Cela pourra t'aider pour terminer l'exercice.

Fonction de transfert & Bode

Fonction de transfert & Bode

Posté par
Araiire : Fonction de transfert & Bode 04-05-18 à 14:06

Bonjour,
Désolé de  ne pas avoir répondu hier, je n'ai pas eu le temps.
Merci beaucoup pour votre aide j'ai réussi ET compris cette question par conséquent (Les deux en même temps c'est mieux ).
Pour le diagramme de Bode, est-ce que vous avez éventuellement des liens sur lesquels ils expliquent comment l'exploiter ?

Posté par
vanoisere : Fonction de transfert & Bode 04-05-18 à 15:26

Citation :
Pour le diagramme de Bode, est-ce que vous avez éventuellement des liens sur lesquels ils expliquent comment l'exploiter ?

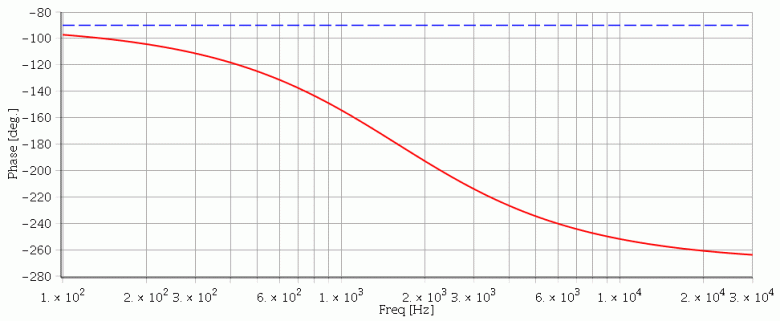
Les deux liens que je t'ai déjà fournis expliquent l'essentiel. Pose si nécessaire des questions précises sur ce que tu ne comprends pas. Pour l'exploitation du diagramme de Bode, il te faut d'abord déterminer la valeur numérique de fo. La situation f=fo, soit x= 1 correspond au maximum du gain et à une phase égale à -180°. Il suffit de déterminer l'abscisse d'un de ces deux points. La courbe du gain étant très "arrondie" au voisinage du maximum, la détermination de l'abscisse du point correspondant à  une phase de -180° conduit à un résultat plus précis. Attention : l'échelle des abscisses est logarithmique ! Tu devrais trouver fo1,6kHz.
Pour les valeurs de Qo et m : il ne s'agit pas de "détermination" mais de "vérification" puisque les valeurs sont déjà connues. Pour la valeur de Qo, le plus simple consiste à déterminer graphiquement les deux fréquences de coupures f1c et f2c correspondant aux limites de la bande passante. Le gain maximum étant de -6dB, les fréquences de coupure correspondent à G=-9dB. Ayant mesuré graphiquement ces fréquences de coupure, le facteur de qualité vérifie :

Q_{o}=\frac{f_{0}}{f_{2c}-f_{1c}}
La démontration de cela est sur un document dont je t'ai fourni la référence.
Je te laisse travailler...

Posté par
boris69re : Fonction de transfert & Bode 12-12-18 à 05:25

Bonjour à tous,
je permet de revenir sur la suite de cet exercice que j'ai essayé de refaire en entier mais je bloque sur la question 5-b.

Selon mes calculs, on trouve effectivement :
Qo= fo/(f2c-f1c), mais uniquement (il me semble) en partant du fait que:

T (sous sa forme complexe)= To/(1+jQo(x-1/x)), comme c'est le cas dans les liens que vous avez partagé pour la démonstration.

Mais je n'arrive pas à avoir ce résultat en partant du fait que:

T (sous sa forme complexe)= ToQo/(1+jQo(x-1/x)). Pouvez m'aider sur ce point svp?

Ps: Désolé pour l'écriture j'ai du mal avec les symboles. Merci d'avance. CDT

Posté par
vanoisere : Fonction de transfert & Bode 12-12-18 à 11:12

Bonjour
Il s'agit juste d'une différence de notation : To n'ayant pas le même sens dans ce problème et dans les documents cités en référence. Ce qu'il faut retenir car valide dans tous les cas :
Les fréquences de coupure correspondent à :

|\underline{T}|=\dfrac{|\underline{T}|_{max}}{\sqrt{2}}

Dans certains problèmes : |\underline{T}|_{max}=T_{o} ; dans d'autres : |\underline{T}|_{max}=T_{o}.Q_{o} .

Posté par
boris69re : Fonction de transfert & Bode 12-12-18 à 14:03

Merci à vous pour votre aide ! C'est super.
Cdt

Posté par
boris69re : Fonction de transfert & Bode 17-12-18 à 10:43

Bonjour,

Une derniere question sur cet exercice svp:
Pour fo =1600Hz, on a un gain correspondant Go=-6dB=Gmax
Donc To=10^(-6/20)=0.5.

Ce résultat me parait anormal compte tenu de précédente valeur de To=1.

Pouvez vous m'éclairer sur ce point svp?
CDT

Posté par
vanoisere : Fonction de transfert & Bode 17-12-18 à 11:47

Dans ce problème :
Gmax=20.log(To.Q) et non 20.log(To) car, comme expliqué précédemment, avec les notations de ce problème qui ne sont pas les plus habituelles :
|\underline{T}|_{max}=T_{o}.Q_{o}   et on a toujours :
G_{max}=20.\log\left(|\underline{T}|_{max}\right)


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !