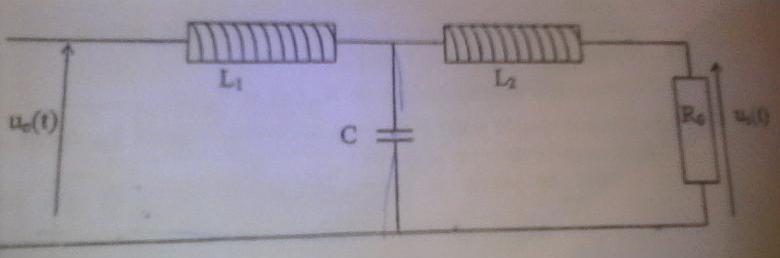
Bonjour
La méthode consiste à déterminer d'abord la tension u_C aux bornes du condensateur puis à considérer que l'ensemble série {L2,R} se comporte comme un diviseur de tension vis à vis de cette tension u_C.
Pour obtenir u_C : deux méthodes possibles :
1° appliquer le théorème de Millman s'il est à ton programme ;
2° commencer par calculer Z1,l'impédance équivalente à l'association {C parallèle (L2-R)} . Ensuite, considérer que l'ensemble série {L1,Z1} se comporte en diviseur de tension vis à vis de la tension d'entrée.
Je te laisse réfléchir à tout cela et proposer une solution.

Salut vanoise
j'essaye avec le théo de millman mais je suis pas certaine du 1er terme du numérateur
u_c=
pour la 2eme méthode Z1=
u_c=
merci de vérifier la démarche

Bonjour
Pour le théorème de Millman : tu as trois branches partant du nœud commun à L1, L2 et C. L'autre borne de L1 est au potentiel ue(t), la deuxième borne de C et la deuxième borne de {L2,R} sont à la masse. Ainsi :



Inutile de trop simplifier avant d'avoir exprimé us(t) en considérant l'ensemble {L2,R} comme un diviseur de tension.

Autre méthode possible :



Formule du diviseur de tension :





On obtient heureusement la même chose mais l'application du théorème de Millman est un peu plus immédiate.

Je te laisse obtenir l'expression de la tension de sortie. Tu as sans doute intérêt à bien revoir le théorème de Millman. La fiche référencée ici pourra éventuellement t'aider :

merci beaucoup pour la rectification et le rappel
maintenant j'applique le diviseur de tension pour l'ensemble L2 ,R vis à vis de u_c
u_s=
je remplace par l'expression obtenu et je trouve H(jw)=

D'accord avec toi. Tu peux éventuellement diviser tous les termes par R, histoire de faire intervenir un "1" au numérateur et au dénominateur.

Je n'ai regardé que ta réponse finale ... et elle me fait mal au yeux.

Elle n'est pas homogène. (c'est le terme j.L1.L2.w³ qui me dérange).

Sauf distraction.

Tu as oublié un C dans le terme en ³...