Niveau licence

Fonction de transfert

Posté par
Jean469 02-06-16 à 14:57

Bonjour,j'aurai si possible besoin d'aide pour la question 1 de cet exo(je posterai les autres questions ensuite).
L'énoncé est:
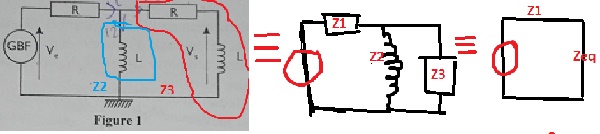
Soit ce quadripôle alimenté par une tension sinusoidal,calculer la fonction de transfert

H(jw)=vs/ve,et mettre sous la forme
$H(jw)=(j(w/w_0))^2/(1-w^2/w_0^2+2mj(w/w_0))$ .

Donner l'expression de w0 en fonction de R et L ainsi que l'expression de m(coefficient d'amortissement).

Quel est le régime de fonctionnement de cet oscillateur?

Et pour l'instant ce que j'ai pu dire est lié à mon schéma.

Selon mon schéma,on a
Zeq=(Z2.Z3)/(Z2+Z3) et vs/ve=zeq/(1+zeq)=1/...

Z3=jLw+R ;Z2=jLw; Z1=R. et 1/Z3=1/(jLw+R)

Enfin j'ai trouvé Vs/Ve=(-(Lw)²+RjLw)/(R²+3RjLw-(Lw)²).
Le régime lui est sinusoïdale je présume,mais je trouve ni w0,ni m.

Fonction de transfert

Posté par re : Fonction de transfert 02-06-16 à 15:42

Bonjour
Selon mes calculs, le numérateur de H fait intervenir uniquement (jLw)².
D'accord avec l'expression de ton dénominateur...
Attention : je n'ai pas le détail de ton calcul mais il me semble bien que ta méthode conduise au potentiel du noeud commun aux deux résistances (potentiel que tu aurais obtenu en une seule ligne par le théorème de Millman) et non à Vs. Il te faut ensuite utiliser la notion de diviseur de tension...

Citation :
et vs/ve=zeq/(1+zeq)=1/...

étourderie je pense : le 1 correspondant à Z1...
Une fois obtenue la bonne expression de H, une division de tous les termes par R² fera apparaître le "1" attendu au dénominateur...

Posté par re : Fonction de transfert 02-06-16 à 18:28

Oui c'est bien z1 pardon,ça parait plus logique que le numérateur soit (jLw)²,car il n'y a pas de j au numérateur.
Je vais bien réfléchir à ma prochaine réponse vu que ma méthode ne mène pas directement à vs/ve.
J'utiliserai Millman plutôt et le diviseur de tension.
Merci pour ton aide

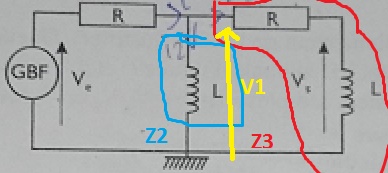
Posté par re : Fonction de transfert 03-06-16 à 15:49

Salut,alors j'ai repris un peu tout ça.
Je pose a=jLw
Ce que j'ai appelé vs/ve c'est V1(voir schéma ci-dessous) maintenant avec V1=Zeq/(R+Zeq)=(1*Ue)/(1+R.Yeq).

Ensuite on a Us=a*U1/(a+R) donc Us=(a*Ue)/(R+a+[R(R+a)/a]+1)=-(Lw)²*Ue/(R²+a*3R-(Lw²)).

On en déduit que H(jw)=(-Lw/R)²/(1+j3Lw/R-(Lw/R)².

En posant ensuite w0=R/L et x=w/w0 on a H(x)=-x²/(1+3jx-x²).

Il ne me reste qu'a déterminer le m et ensuite j'aurai fini avec le 1) vu que j'ai le w0 .

Pour l'instant je passe aux autre questions que je posterai plus tard ou demain.

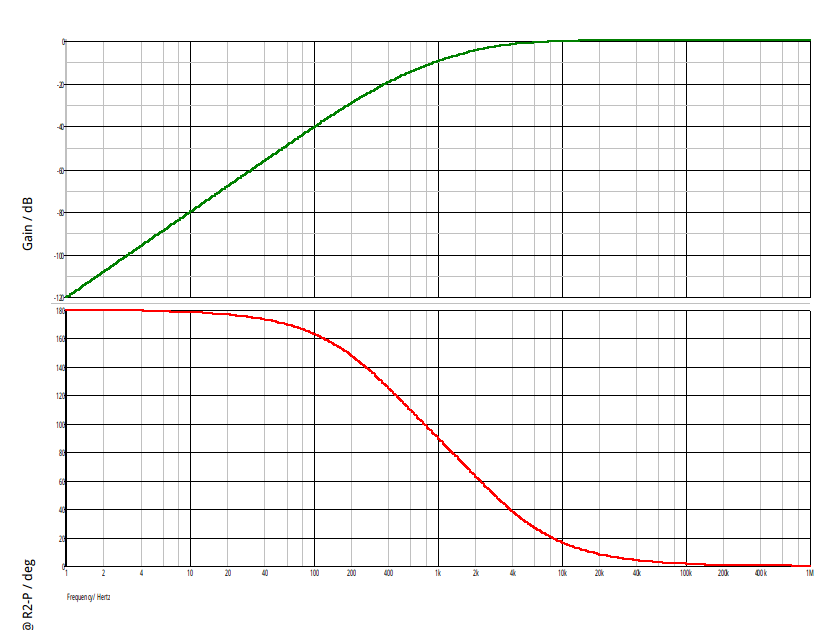
Fonction de transfert

Posté par re : Fonction de transfert 03-06-16 à 16:07

Bonjour
OK pour ton expression de H et pour celle de w_o.
De façon évidente : m=2/3...

Posté par re : Fonction de transfert 03-06-16 à 16:22

Pardon ! 2m = 3 donc m=3/2
Désolé !

Posté par re : Fonction de transfert 10-06-16 à 16:51

Merci pour ton aide vanoise,ils m'ont demandé aussi le module,l'argument et l'expression de $w_c$ (pulsation de coupure) en fonction de w0.
En rappelant qu'à $w=w_c$ |H(jw)|=Hmax/racine(2).
Et j'ai pu trouvé l'argument et le module qui valent:
$|H(jw)|=\dfrac{\left (\dfrac{\omega}{\omega_0} \right )^2}{\sqrt{\left (1-\dfrac{\omega^2}{\omega_0^2} \right )^2+\dfrac{9 \cdot \omega^2}{\omega_0^2}}}$

$\phi=\pi -arctan \left ( \dfrac{3 \cdot \omega \ \omega_0}{\omega_0^2-\omega^2} \right )$ ,mais wc je sais pas.
Ensuite vu que H(jw)=H(x)=(H0*-x^2)/(-x^2+1+j(x/Q)) avec x=w/w0 c'est un passe haut.

Posté par re : Fonction de transfert 10-06-16 à 20:00

Bonjour
Pour étudier les variations du module, tout à tout intérêt à transformer l'expression de façon à avoir un numérateur constant. En divisant tout les termes par x² puis en posant y = 1/x, on obtient :

$|\underline{H}|=\frac{1}{\sqrt{\left(\frac{1}{x^{2}}-1\right)^{2}+\frac{9}{x^{2}}}}=\frac{1}{\sqrt{\left(y^{2}-1\right)^{2}+9y^{2}}}=\frac{1}{\sqrt{y^{4}+7y^{2}+1}}$
Il suffit alors d'étudier les variation de $P(y)=y^{4}+7y^{2}+1$ en fonction de y pour en déduire celle du module de H en fonction de x.
La dérivée par rapport à y vaut :

$P'(y)=4y^{3}+14y=2y\left(2y^2+7\right)$
P'(y) est nul quand y tend vers zéro donc quand x tend vers l'infini et est positif par ailleurs ; le module de H est donc fonction monotone décroissante de y donc fonction monotone croissante de x : cela confirme le fait que le filtre est un passe haut. Dans ces condition la valeur maximale du module de H est obtenue quand x tend vers l'infini :

$H_{max}=1$
La pulsation de coupure est obtenue pour : $|\underline{H}|=\frac{1}{\sqrt{2}}$ soit pour P(y) = 2 soit pour :

$y^{4}+7y^{2}=1$

$y^{2}=\frac{\sqrt{53}-7}{2}=\frac{1}{x^{2}}$
Numériquement :

$x=\sqrt{\frac{2}{\sqrt{53}-7}}\approx2,67$

Ce qui conduit à $\omega_{c}\approx2,67\omega_{o}$

Voici le diagramme de Bode de ce filtre dans le cas particulier $f_{o}=1000Hz.$

Fonction de transfert