Inscription / Connexion Nouveau Sujet
Flux du champ Électrique
Bonjour à tous ,
SVP comment calculer le flux du champ électrique ?
Exercice
Un champ électrique dérive d'un potentiel V et qui présente une symétrie de révolution autour de l'axe (Oz) . On utilise le système de coordonnées polaires ( r ,  )
)
et dans ce système de coordonnées V a pour expression :
V= k(3cos2-1)/r3
1) Déterminer les composantes du champ électrique
Réponses j'ai trouvé :
Er=3k(3cos2-1)/r4
et E =3k(sin2
=3k(sin2 )/r4
)/r4
2)Calculer le flux de ce champ à travers une calotte sphérique centrée en O , de révolution autour de l'axe (Oz) et dont le rayon est vu du centre O sous l'angle 2
Besoin d'indication pour cette 2eme question Svp . Perso je connais juste la formule  =
=
 E.dS Avec E et dS en Vecteurs
E.dS Avec E et dS en Vecteurs
Bonjour
= Err2sin
 d
d d
d
+E rsin
rsin drd
drd
Voilà ce que je trouve . mon soucis est maintenant d'intégrer sur quelles bornes pour chaque variable .
Hum hum ... 2 questions pour te guider:
- Le vecteur surface élémentaire étant porté la la normale au plan contenant cette surface, dans le cas de la calotte est colinéaire à ?
- Pour la calotte, r est constant,  varie de 2 à 2
varie de 2 à 2 , et
, et  varie de ?
varie de ?
On va t'aider ... sois rassuré 
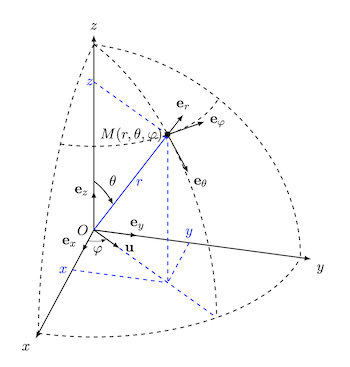
En regardant la figure:
- quel est le vecteur normal (perpendiculaire) à la sphère en M?
(la surface est la même avec ou bien sans le champ électrique donc le vecteur orientant la surface est sans rapport avec )
- petite rectification avec ce que j'ai écrit plutôt la calotte ayant pour axe Oz,  va effectivement tourner de 0 à 2
va effectivement tourner de 0 à 2 ,
,
- en supposant par exemple que le point M se trouve sur le "bord" de la calotte, combien vaut  en se point et donc pour parcourir toute la calotte
en se point et donc pour parcourir toute la calotte  varie de 0 à ?
varie de 0 à ?
Bonjour,
petite rectification avec ce que j'ai écrit plutôt la calotte ayant pour axe Oz,
 va effectivement tourner de 0 à 2
va effectivement tourner de 0 à 2 
Confusion "logique" ! Le
 du message de départ est le
du message de départ est le  des coordonnées sphériques.
des coordonnées sphériques.On va t'aider ... sois rassuré

En regardant la figure:
- quel est le vecteur normal (perpendiculaire) à la sphère en M?
(la surface est la même avec ou bien sans le champ électrique donc le vecteur orientant la surface est sans rapport avec
- petite rectification avec ce que j'ai écrit plutôt la calotte ayant pour axe Oz,
 va effectivement tourner de 0 à 2
va effectivement tourner de 0 à 2 ,
,- en supposant par exemple que le point M se trouve sur le "bord" de la calotte, combien vaut
 en se point et donc pour parcourir toute la calotte
en se point et donc pour parcourir toute la calotte  varie de 0 à ?
varie de 0 à ?
________________
***Edit gbm > MEV : est-ce que tu pourrais préciser ton niveau d'études sur ton profil ("autre" c'est trop vague)
 ?***
?******Edit gbm > MEV : est-ce que tu pourrais préciser ton niveau d'études sur ton profil ("autre" c'est trop vague)
 ?***
?***le vecteur normal à la sphère en M est ez

En M le vecteur normal à la sphère (et dirigé vers l'extérieur) est
Par ailleurs comment comprends tu cette portion de l'énoncé:
e révolution autour de l'axe (Oz) et dont le rayon est vu du centre O sous l'angle 2

le vecteur normal à la sphère en M est ez

En M le vecteur normal à la sphère (et dirigé vers l'extérieur) est
Par ailleurs comment comprends tu cette portion de l'énoncé:
e révolution autour de l'axe (Oz) et dont le rayon est vu du centre O sous l'angle 2

Je comprends par cette phrase que
 va varier de 0 à 2
va varier de 0 à 2
Bonjour
 d
d d
d
+E
 rsin
rsin drd
drd
Voilà ce que je trouve . mon soucis est maintenant d'intégrer sur quelles bornes pour chaque variable .
 va varier de 0 à 2
va varier de 0 à 2 normalement .
normalement .
et concerenant l'expression à intégrer c'est juste celle en rouge parce que r est constant .
En continuant d'intégrer ( r constant ,  de 0 à 2
de 0 à 2 et
et  de 0 à 2
de 0 à 2 , j'obtiens cette expression du flux :
, j'obtiens cette expression du flux :
(2k /r2)[4-cos(2
/r2)[4-cos(2 )(1+3cos(4
)(1+3cos(4 ))+4(1-cos3(2
))+4(1-cos3(2 ))]
))]
Soit
J'ai intégré la derniére expression et j'ai trouvé l'expression qui est plus haut .
En continuant d'intégrer ( r constant ,
 de 0 à 2
de 0 à 2 et
et  de 0 à 2
de 0 à 2 , j'obtiens cette expression du flux :
, j'obtiens cette expression du flux :
(2k[sm Jb]pi[/smb]/r2)[4-cos(2
 )(1+3cos(4
)(1+3cos(4 ))+4(1-cos3(2
))+4(1-cos3(2 ))]
))]J'ai appliqué et j'ai trouvé ça
En continuant d'intégrer ( r constant , de 0 à 2 et de 0 à 2 , j'obtiens cette expression du flux :
(2k/r2)[4-cos(2)(1+3cos(4))+4(1-cos3(2))]
Bon alors reprenons, (j'ai un peu de boulot ces jours ci ... après une semaine de congés)
Tu écrivais
concerenant l'expression à intégrer c'est juste celle en rouge parce que r est constant
En fait c'est même plus direct que cela:
Avec
et
En remarquant que

Euh pas tout à fait, si la variable devient cos les bornes d'intégration passent de [0 , 2
les bornes d'intégration passent de [0 , 2 ] à [1 , cos2
] à [1 , cos2 ]
]
Tout compte fait , je trouve vraiment une expression plus simple du flux électrique :
 =(3k
=(3k /r2)sin2
/r2)sin2 sin4
sin4





