Inscription / Connexion Nouveau Sujet
Flux à travers un cadre conducteur carré.
Bonsoir,je poste ce message car j'aurai besoin du corrigé de cet exo que mon prof n'a pas corrigé .
J'ai toutefois tenté de le faire.
Le voici:
Un cadre conducteur carré de côté a et de résistance linéaire r(ohm/m)se déplace avec une vitesse v dans le plan xOy ou existe un champ magnétique B=Bz.ez.
I)B=B0.
1)Calculer le flux de B à travers le cadre.
2)Donner la valeur de la f.e.m induite.
3)Calculer I.
II)B=B0.coswt.
1)Donner la valeur de la f.e.m induite.
2)Calculer le courant I.
3)Donner le sens du courant pour t=T/8 et pour t=3T/8.
Et voici mes réponses:
=
B.n.dS (n et B vecteurs)=
,
(t)=.
2)f.e.m=|d/dt|=|
[/dt|.
c=(t+dt)-(t).
Et (t+dt)=(t).
Car tout le circuit en translation n'est pas fonction du temps.
_c=0=>f.e.m=0.
Puis on sait que la f.e.m=
-
/t.ndS+(v^B)dl.
dB/dt= =>fem=...
^
=...=>
3)I=e/r=0.
II)B=B0.coswt.
fem=(voir formul ci-dessus).
v^B=0(v et B vecteurs)=>fem=-B/t.n.dS.
B(vecteur)=/t(B0.coswt.ez+B0.coswt.ey).*
Et comme n=ez,B/t=.n=
-w.B0.sinwt.
et fem=-dS=-w.B0.coswt.a^2.
2)I=e/R=fem/4r.a=-w.B0.coswt.a/4r.
3)Pour t=T/8 et wt=2pi/T,wt=pi/4,cospi/4=racine(2)/2,je fais pareil pour les autre t,et je dessinerais le graphe(mais si j'ai un problème je le posterais).
Bonjour
D'accord avec toi pour la première question : le flux magnétique à travers le circuit ne varie pas (ou si tu préfères : le flux coupé est nul) : pas de courant induit.
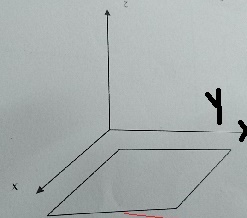
Pour la partie II : le flux magnétique varie : création de courant induit. Pour la mise en équation, il est indispensable d'orienter le circuit, ce qui n'est pas fait sur ton schéma...
Bonjour vanoise,pour le II) j'ai fait quelques fautes de frappes,j'espère que vous vous retrouverez.
Pour le I) tout est bon?
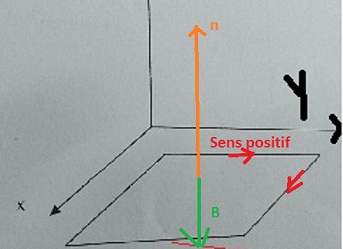
Sinon mon circuit orienté le voici:
Bonjour
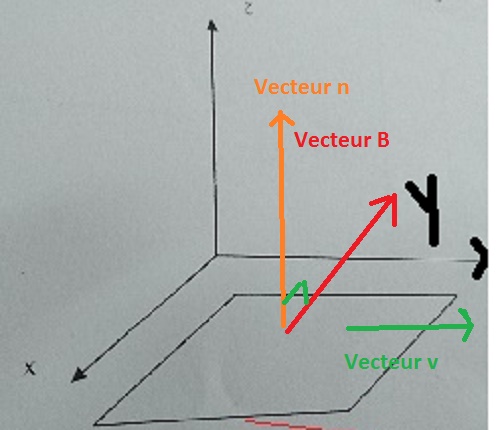
Je viens de relire l'énoncé : les vecteurs B et n ont même direction me semble-t-il.
Pour le sens du vecteur n, tout dépend du sens positif de circulation de courant choisi pour le cadre . Tu n'indiques pas ce sens sur ton schéma.
Je crois que tu n'as pas très bien compris ton cours... Le sens du vecteur B est imposé par l'expérience (les pôles nord et sud de l'aimant, le sens du courant dans un électroaimant...) : ici, selon l'énoncé, il a le sens de ez. Le sens du vecteur n est lié au sens choisi de circulation le long du circuit par la règle du "tire-bouchon de Maxwell" ou "de la main droite" : si tu veux que le vecteur n soit orienté vers le haut comme sur ton schéma, il faut inverser le sens de circulation (flèches rouges).
Ceci étant supposé fait, les vecteurs n et B sont tous les deux orientés suivant ez :
Force électromotrice :
Loi de Pouillet donnant l'intensité instantanée avec R résistance totale du cadre :
Annuler
connectez vous