Inscription / Connexion Nouveau Sujet
Filtre passe bas
Bonjour,
Dans un exercice dans lequel je dois déterminer la réponse impulsionnelle d'un filtre passe bas idéal de bande passante B, on me dit que dans un tel cas, on a et
. De plus, on me représente la chose comme sur la figure ci-jointe.
Je ne comprends pas toutes ces infos.. Pourriez-vous m'expliquer comment on y parvient svp?
Merci d'avance.
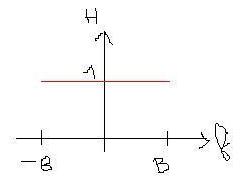
La figure ne fait que reprendre les informations de l'énoncé (même si elle ne fait pas apparaître la phase, mais ça n'est pas important ici), à savoir la largeur de la bande et l'amplitude du filtre (constante) sur cette bande.
Comment as-tu l'intention de t'y prendre pour calculer la réponse impulsionnelle de ce filtre?
On ne l'"obtient" pas puisque c'est ainsi que l'on définit un filtre passe-bas idéal...
Rappelle-toi seulement la façon dont intervient la fonction de transfert dans le calcul du signal en sortie du filtre:
A partir de là, il est facile d'imaginer l'effet du filtre sur le signal d'entrée en regardant sa représentation graphique. Il laisse passer les fréquences basses sans les altérer (
) et supprime totalement les fréquences hautes (
).
Mais ce qu'on te demande c'est de calculer la réponse impulsionnelle.
Tu mets dans ton explication à la fois et
...

De plus, pourquoi , qui est la fonction de transfert, signifie que le filtre laisse passer les basses fréquences? Je ne comprends pas l'interprétation en fait.
Il ne t'auras pas échappé que H(f) prend des valeurs différentes selon que et
?
Regarde la figure ci-dessous qui représente l'effet du filtre sur un signal quelconque.
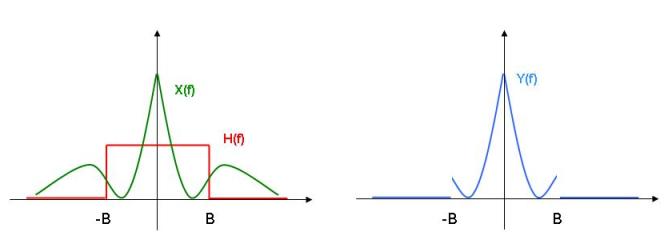
Je ne comprends pas trop à quoi correspondent les et
. Si j'ai bien compris, l'une de ces bornes prend pour valeur
puisqu'il s'agit là d'un passe bas non?
Pas du tout. B est une valeur fixe, c'est la largeur de la bande, c'est à dire toutes les fréquences que l'on souhaite conserver.
On parle de filtre passe-bas lorsque les fréquences préservées sont situées autour de zéro. Ici, précisément, les fréquences conservées appartiennent à [-B,B].
basses fréquences :
hautes fréquences :
(pour schématiser)


