Inscription / Connexion Nouveau Sujet
Filtre passe bande
Bonjour,
On me demande de trouver l'expression du gain d'un filtre passe bande RLC, R étant en série avec L//C. On me précise qu'il y a 1 zéro et 2 pôles.
Après calcul, je trouve bien les 2 pôles, mais en aucun cas le "zéro" (1 au numérateur)... Avez-vous une explication ?
Merci d'avance.
Bonsoir,
Je ne trouve pas 1 au numérateur...enfin, ça dépend du dénominateur évidemment...
(si j'ai bien compris pour le circuit)
auquel cas, on a 2 pôles et 1 zéro effectivement...
En dehors du fait que l'écriture est extrêmement maladroite, je ne suis pas d'accord avec ce résultat...
Finalement je trouve bien comme vous aussi mais... Je pense que mon autre expression reste correcte !
Oui, effectivement, j'avais fait le calcul un peu vite et une erreur de signe s'était fâcheusement glissée dans le résultat...
Mais il n'empêche qu'il ne faut pas la laisser sous cette forme un peu "tarabiscotée", surtout si on veut trouver des pôles et des zéros.
Le but étant de tracer le diagramme de Bode, je pense au contraire que cette forme peut faciliter les choses pour l'étude du module (trouver sa valeur max, pour quelle fréquence, fréquences de coupure,...). Car au final, trouver les pôles et le zéro n'a pas d'utilité dans ce cas si ?
Dans ce cas, les pôles et les zéros ne sont pas d'une grande utilité car ils servent en général à l'étude de la stabilité. Le circuit étant passif, il est inconditionnellement stable.
Pour le diagramme de Bode, tu as bigrement intérêt à utiliser la forme que j'ai donnée...
Pour tracer un diagramme de Bode.
Si on a Vs/Ve = 1/(1 + pT)
Dans le diagramme asymptotique :
On a une "cassure" à -20 dB par décade à partir de w = 1/T pour le gain et on a une "cassure" de - 90° dans la phase à partir de w = 1/T
Facile ... Mais, dans l'expression Vs/Ve = 1/(1 + pT) (p = jw en sinusoïdal), on a, bien entendu, T = constante (dépendant des composants R,L et C, mais indépendant de w)
Si le "T" est fonction de w comme quand tu écris 1/(1 + jR(wC - 1/(wC)), alors c'est bernique pour tracer les diagrammes asymptotiques, du moins sans calculs.
-----
Par contre, avec vs/ve = pT1/(1 + A.p + B.p²) (avec p = jw en sinusoïdal)
On a un zéro à l'origine (donc pente à +20 db et phase de + 90° dès l'origine) et on a un double pôle en w = 1/racine(B) et on peut donc tracer les diagrammes asymptotiques de gain et de phase sans aucun calcul.
Sauf distraction 
La forme que tu as tenté d'utiliser est utile si tu l'écris complètement sous la forme "canonique" du filtre passe-bande, à savoir :
Mais, comme l'écrit J-P, on ne sait pas tracer le diagramme de Bode à l'aide de cette forme (sans caculs).
Sous l'autre forme, on sait tracer le diagramme de Bode. Il ne s'agit que d'une forme asymptotique parce que la forme exacte dépend beaucoup de la valeur de Q quand on écrit le dénominateur sous la forme :
La forme est normalement étudiée en cours selon les valeurs de Q.
On l'écrit aussi :
Ok. J'aimerais essayer les deux méthodes, celle avec calculs et l'autre sans.
Pouvez-vous me donner quelques indications sur les calculs à faire, j'ai finalement du mal à exploiter l'expression pour tracer Bode...(j'ai la seulement les fréquences caractéristiques..).
Pour l'autre méthode, je n'ai pas vu comment faire le teacé sans calculs. Pouvez-vous expliciter sur mon exemple svp ?
Merci pour votre aide.
On peut le faire, moyennant quelques calculs, avec la forme que tu as voulu utiliser.
On a :
En posant :
et :
on peut écrire :
ou encore :
Donc :
Maintenant, il faut trouver le comportement asymptotique moyennant quelques approximations.
(que je ferai si tu ne sais pas faire)...
Merci beaucoup pour ces détails. Malheureusement, je vais encore vous embêter.. Je ne vois en effet pas comment procéder pour le comportement asymptotique. Les seules choses que j'ai trouvées, c'est que lorsque tend vers l'infini et vers 0, le module du gain tend vers 0. Au passage, je préfère raisonner en termes d'
sur le papier, simple question d'habitude.
PS : une méthode plus simple était donc envisageable ?
On peut le faire, moyennant quelques calculs, avec la forme que tu as voulu utiliser.
On a :
En posant :
et :
on peut écrire :
ou encore :
Donc :
Maintenant, il faut trouver le comportement asymptotique moyennant quelques approximations.
On va chercher le comportement dans une zone telle que
donc :
Si f est telle que :
La condition la plus restrictive est donc .
D'où :
Donc, la pente est de 20 dB/décade (si la fréquence est multipliée par 10, on a une augmentation de 20 dB)
On va chercher de même le comportement dans une zone où
donc :
Si f est telle que :
La condition la plus restrictive est donc .
D'où :
Donc, la pente est de -20 dB/décade (si la fréquence est multipliée par 10, on a une perte de 20 dB).
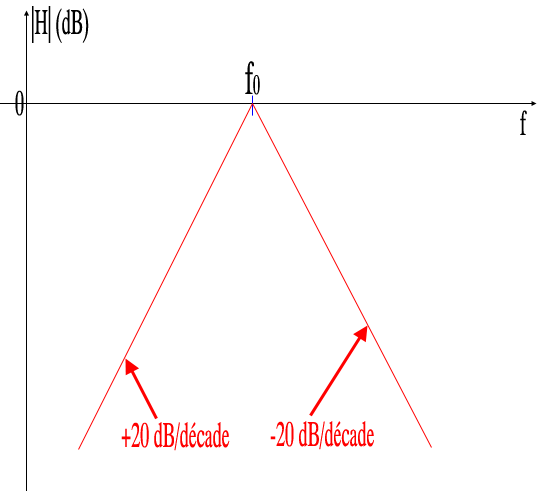
Et, pour f = f0, on a |H| = 1 donc 0 dB. Les asymptotes passent par le point (f0 ; 0).
On obtient donc quelque chose qui ressemble au schéma joint. Au voisinage de f0, on n'est pas "collé" aux asymptotes. On ne connaît pas exactement la forme de la courbe au voisinage de f0. Il s'agit d'asymptotes donc la courbe s'en approche pour f << f0 et pour f >> f0.
On peut le trouver plus facilement avec l'autre forme :
Au numérateur, on voit immédiatement une pente de +20 dB/décade et au dénominateur (2nd ordre), on commence par un plateau à 0 dB pour finir par une pente de -40 dB/décade à .
Il est préférable de l'écrire sous forme "canonique" pour avoir quelque chose de plus explicite...
Mais encore faut-il l'avoir étudié en cours au préalable ...
J'espère que c'est à peu près clair.
La suite dans un autre message...
Merci pour cette réponse ! Je regarde ça plus attentivement en fin d'aprem, et je répondrai dans la foulée. Question entre temps : pouvait-on partir directement de la formule donnée au message du 30/03 à 20h36 ? Si oui, l'étude aurait-elle été plus rapide/simple ?
Alors, un premier commentaire : après chacun des deux cas envisagés, vous écrivez "Donc, la pente est de + ou -20 dB/décade". Que fait-on de l'autre terme de la somme, -20log(Q/fo) ?
Bonjour matix, c'est possible de vous contactez a une adresse j'aurais besoin d'un renseignement svp 
et :
Les deux termes et
sont utilisés pour tracer les deux asymptotes.
Le résultat final n'est pas celui que j'ai rapidement tracé précédemment. Pour avoir une idée de la courbe (c'est asymptotique), il faut savoir ce qui se passe autour de f0 parce que les résultats que nous avons obtenus, sont valables pour f << f0 et f >> f0. Donc ces asymptotes ne nous fournissent pas d'indications sur la courbe aux alentours de f0 parce que les approximations utilisées ne sont plus valables.
Cela vient du fait que le comportement de la courbe au voisinage de f0 dépend beaucoup de la valeur de Q.
Ok merci... Mais du coup, quand on me demande de tracer le diagramme de Bode, que suis-je censé faire alors ?
Je commence à avoir un doute...
Normalement, quand on parle de diagramme de Bode, il s'agit de diagrammes asymptotiques donc peu précis surtout pour la phase. Et pour le circuit du second ordre, c'est encore pire en présence de surtension (Q > 1/ (2) ) parce qu'on ne peut rien tracer autour de f0.
(2) ) parce qu'on ne peut rien tracer autour de f0.
Les diagrammes de Bode sont faciles à tracer pour les circuits du 1er ordre ou décomposables en circuits du 1er ordre.
Dans cet exercice, je commence à me demander si ce sont les diagrammes asymptotiques qu'on demande... Ne faudrait-il pas tracer (par le calcul) les diagrammes amplitude/fréquence et phase/fréquence ?
Y a-t-il des valeurs numériques pour R, L, C ?
Alors, je rajoute des précisions. Citant l'énoncé, on me demande de dessiner le diagramme de Bode, incluant module + argument. Et on me donne des valeurs numériques pour R,L et C, mais uniquement pour l'argument. Je n'ai pas d'infos supplémentaires... Qu'en pensez-vous ?
Et on me donne des valeurs numériques pour R,L et C, mais uniquement pour l'argument
On n'a pas le droit de s'en servir pour le module ?
Les pôles ont été calculés (sauf erreur de ma part). Quelles sont les valeurs trouvées ?
On n'a pas le droit de s'en servir pour le module ?
Curieusement non, et c'est écrit en gras. Je ne comprends pas pourquoi, mais bon...
Du coup, est-il intéressant que je calcule les valeurs numériques des deux pôles ?
Du coup, est-il intéressant que je calcule les valeurs numériques des deux pôles ?
Cela est-il demandé ?
Mais il faut écrire le dénominateur sous la forme
en posant :
et :
En posant
Trinôme du second degré à coefficients réels (racines conjuguées si
 < 0).
< 0).
D'où :
Ou :
Dans le premier cas, on pourra écrire la fonction de transfert avec trois fonctions du premier ordre :
et il n'y a aucune difficulté pour tracer le diagramme de Bode (à condition de connaître
 N,
N,  1,
1,  2).
2).
Dans le deuxième cas, on aura les asymptotes vues précédemment :
et :
et le point (f0 ; 0 dB) mais on ne saura pas le relier aux asymptotes parce que la forme de la courbe dépend beaucoup de la valeur de Q.
Sans la valeur de Q, on ne peut pas faire grand-chose donc, comme , il faut utiliser les valeurs de R, L, C...
Le calcul des pôles n'est pas demandé non. Je suis "juste" censé tracer Bode.
Bon, soyons honnête, je me perds un peu là.. Je le rappelle, mais on me dit d'utiliser les valeurs numériques de R, L et C uniquement pour le tracé de la phase. Mais commençons par le module déjà.
J'en étais resté au fait que selon \omega par rapport à \omega_0, on avait :
ou
Désolé d'insister, mais à partir de là, je ne peux pas le tracer ? J'avoue rester perplexe devant ma feuille semi-log...
Je reviens à ce que j'ai dit précédemment : sans la valeur de Q, on ne peut même pas tracer les asymptotes.
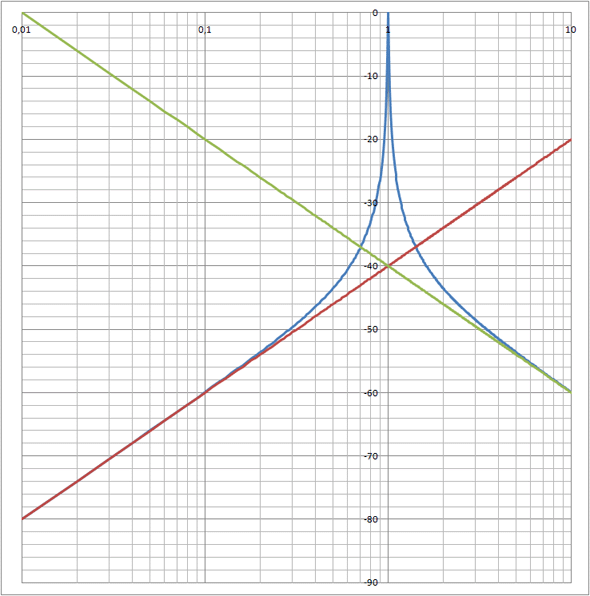
Les deux asymptotes passent par le point ( f0 ; -20 log(Q) ) et on une pente de 20 dB/décade pour l'une et une pente de -20 dB/décade pour l'autre.
Ci-joint un exemple (Q = 100) avec la courbe et les asymptotes. L'axe des fréquences est logarithmique et est gradué en f/f0 (f/f0 = 1 ==> f = f0) .
Et comment arrive-t-on à mettre sous cette forme 3$\frac{j\,\frac{\omega}{\omega_N}}{(1\,+\,j\frac{\omega}{\omega_1})\,(1\,+\,j\frac{\omega}{\omega_2})} ?
Ca ne me paraît pas du tout évident...
 N est ce que les électroniciens appellent "la pulsation de coupure" du numérateur.
N est ce que les électroniciens appellent "la pulsation de coupure" du numérateur.
Autrement dit,
Ou, si on écrit le numérateur . Donc pour
, le numérateur (en module) sera égal à 1 donc 0 dB. Donc la pulsation
est le point d'intersection de l'asymptote du numérateur (20 dB/décade) avec l'axe des fréquences (0 dB)
Bien que le texte soit en espagnol, cela correspond à l'un des cas que j'ai évoqué (pôles réels) dans lequel la fonction de transfert peut s'écrire avec 3 fonctions du 1er ordre. On peut alors tracer le diagramme de Bode sans problème. C'est beaucoup moins simple quand les pôles sont complexes.
Cela dépend de la valeur de Q.
Et dans mon cas, les pôles sont complexes... Bon, essayons de réorganiser tout cela pour que je puisse tracer ces diagrammes d'ici ce soir (pour demain...).
1) Les valeurs des composants : R=50 ohms, L=100mH et C=1uF.
2) Ensuite, je pense qu'il faut commencer par mettre en forme "normalisée" mon gain en tension pour pouvoir l'exploiter, chose que je ne vois pas comment réaliser.
3) ...
Pour le numérateur, c'est ce que j'ai expliqué dans l'avant-dernier message et, pour le dénominateur, il s'agit du cas où les racines (pôles) sont réelles et on factorise le dénominateur avec ces racines (trinôme du second degré).
Pour le dénominateur, en partant de quel trinôme ? Pour ma part, je ne connais pas ce type de factorisation... J'avais appris, si je me souvient bien, que pour un trinôme du second degré de la forme , on pouvait le factoriser ainsi :
si
et
en sont les racines. Non ?
Ok, jusque là, ça va donc. J'ai la forme normalisée.
A partir de là, que faut-il faire pour tracer la courbe ?
en posant :
et :
En posant s = j :
:
parce que
On peut poser :
Et :
On peut alors écrire :
On a alors :
Asymptotiquement :
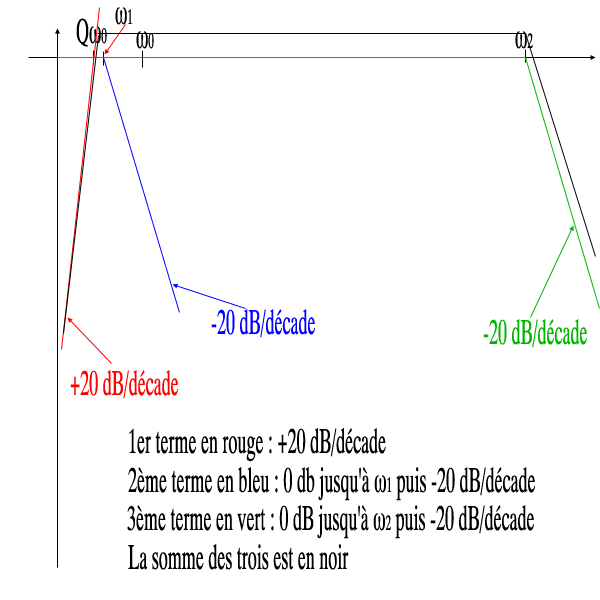
lLe premier terme ==> +20 dB/décade
lLe deuxième terme ==> O dB jusqu'à  1 puis -20 dB/décade
1 puis -20 dB/décade
le troisième terme ==> O dB jusqu'à  2 puis -20 dB/décade
2 puis -20 dB/décade
Donc en faisant la somme, on commence par +20 dB/décade, puis un plateau avec une pente à 0 dB (20 - 20), et pour finir une pente à -20 dB/décade (0 - 20).
Cela doit donner quelque chose comme ça (sauf erreur de ma part)
La figure n'est pas à l'échelle exacte.