Inscription / Connexion Nouveau Sujet
Je n'ai pas encore étudié la phase (je le fais avant minuit), mais j'ai fait une simulation sous PSpice, et ça devrait donner quelque chose comme sur la pièce jointe...
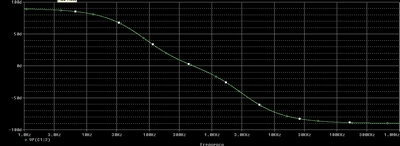
Oui, cela va de +90° à -90° effectivement...
La phase s'écrit :
Asymptotiquement, donne :
jusqu'à
pour
En fait pour , on a
De même, asymptotiquement, donne :
jusqu'à
pour
En fait pour , on a
Je reviens rapidement sur le module : quand on a les termes en -10log(...), pourquoi parler d'une pente de -20 dB/dec ?
Autre chose :
Le "plateau horizontal" est quasiment au niveau 0 dB.
Tout dépend où se place Q\omega_0 par rapport à \omega_1 non ? Si \omega_1 en est "assez" écarté, la pente à +20dB/dec va monter bien plus haut que 0dB avant d'établir le "plateau" non ? Si non, je n'ai rien compris.

Et encore autre chose: je viens de calculer et
avec les valeurs numériques qu'on a. Je trouve deux valeurs négatives...

Je reviens rapidement sur le module : quand on a les termes en -10log(...), pourquoi parler d'une pente de -20 dB/dec ?
Pour
- Si
- Si
On obtient donc, malgré les apparences, une pente de -20 dB/décade pour
Aux alentours de
Tout dépend où se place Q\omega_0 par rapport à \omega_1 non ? Si \omega_1 en est "assez" écarté, la pente à +20dB/dec va monter bien plus haut que 0dB avant d'établir le "plateau" non ? Si non, je n'ai rien compris.
Tu as parfaitement compris mais il se trouve que
Ok merci, ça marche. Mais je ne comprends pas pourquoi on me précise d'utiliser les valeurs numériques que pour la phase...
Et concernant les valeurs de omega 1 et 2 alors ? J'essaie de tracer la phase avec les données, et omega négatifs ne m'aident guère...
Et encore autre chose: je viens de calculer

C'est normal... Les racines sont négatives pour les racines réelles et les racines complexes sont à partie réelle négative. C'est une condition de stabilité. Le circuit étant passif, il est inconditionnellement stable donc on obtient des racines négatives (ou à partie réelle négative dans le cas de racines complexes ce qui n'est pas le cas ici).
J'ai peut-être été un peu rapide...

En posant s = j
 :
:
On trouve donc des racines
On pose :
Donc :
Or le produit des racines
Donc il reste :
Donc :
Et concernant les valeurs de omega 1 et 2 alors ? J'essaie de tracer la phase avec les données, et omega négatifs ne m'aident guère...
J'ai répondu dans mon dernier message à ce sujet.
En fait, les racines sont
On pose :
Mais je ne comprends pas pourquoi on me précise d'utiliser les valeurs numériques que pour la phase...
Probablement pour avoir une courbe plus précise...
Si on se contente des asymptotes pour la phase, on a une courbe un peu "succincte"...
Non ce n'est pas trop tard, c'est pour demain finalement.
Ok pour les omega, mais je ne connais pas cette théorie sur la stabilité... Un peu dommage.
Au final, j'obtiens comme valeurs :
Omega1= 513 rad/s
Omega2=19487 rad/s
On est d'accord ?
Si oui, je reviens faire un bilan en fin d'aprem, voire avant.
Plus que succinte même vu que la courbe peut aussi bien avoir son "plateau" proche de 0dB que très éloigné... !!
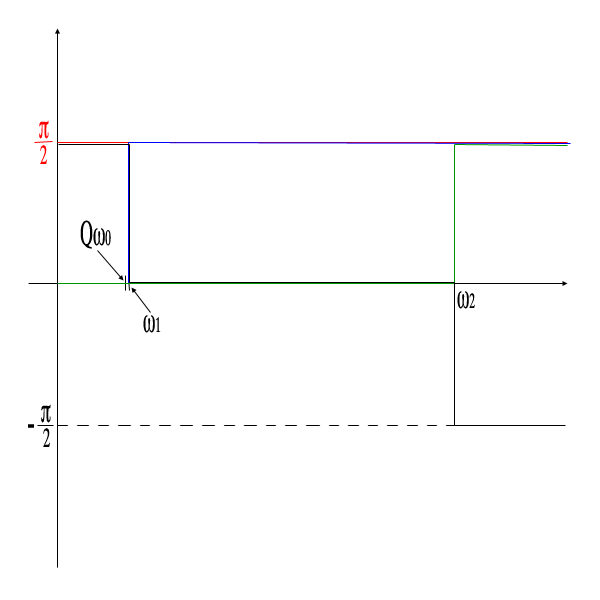
Pour la phase, on obtient la courbe asymptotique suivante :
- numérateur en rouge (imaginaire pur ==> \frac{\pi}{2})
- terme en  1 ==> en bleu
1 ==> en bleu
- terme en  2 ==> en vert
2 ==> en vert
et on fait :
en noir
Ce n'est pas très visible parce que les courbes se superposent.
Pour et
, je réponds un peu plus tard (vers 17 h au plus tard)
Ça marche, et merci pour les détails.
Autre remarque concernant le tracé du module : une fois encore, selon les valeurs de omega1 et omega2, les pentes à -20dB/dec représentées pour la compositon du module "total", n'apparaissent pas forcément parallèles comme sur le schéma de la page précédente... Non ?
Et tant que j'y suis, autre chose qui me dérange, pour la phase cette fois-ci.
En traçant une approximation de la courbe réelle (donc plus vraiment les asymptotes), on devrait avoir, sauf erreur, par exemple, en omega=omega2, theta=+pi/4 - artg(w2/w1). Or, si je regarde le tracé que j'ai fait en m'aidant des asymptotes, je tombe sur -pi/4 en w=w2...
Je viens de revenir...
Effectivement, on a :
Je réponds pour la phase :
Pour
Mais est grand...
Donc :
Autre remarque concernant le tracé du module : une fois encore, selon les valeurs de omega1 et omega2, les pentes à -20dB/dec représentées pour la compositon du module "total", n'apparaissent pas forcément parallèles comme sur le schéma de la page précédente... Non ?
Les droites avec une pente de -20 dB/décade (vrai pour +20 aussi) sont parallèles puisqu'elles ont la même pente.
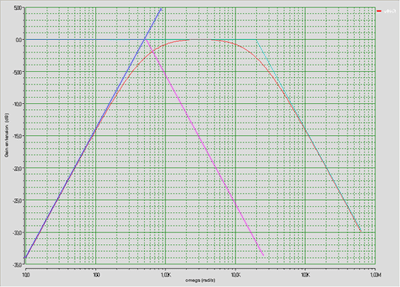
Tu trouveras (un peu petit mais je ne peux pas faire mieux) la vraie courbe (en rouge) avec les asymptotes qu'il faut additionner...
On commence par +20 dB/décade avec la bleue.
A ou
(
, la pente de +20 dB/décade est annulée par la pente à -20 dB/décade (violet) donc une ligne horizontale à 0 dB à peu près (très légèrement au-dessus en réalité).
Cela continue jusqu'à où on a une pente de -20 dB/décade (couleur cyan).
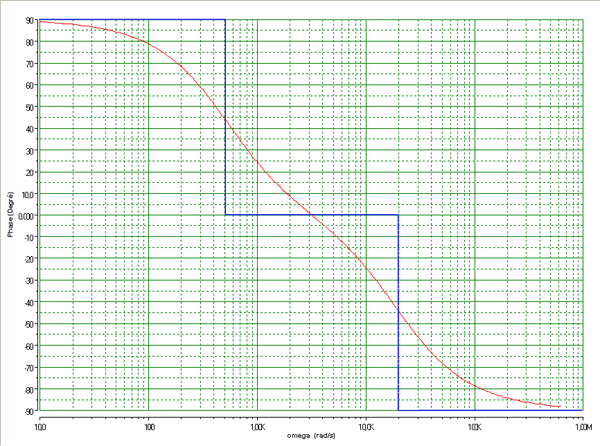
Et la phase avec la vraie courbe et la réponse asymptotique
(la graduation de la phase est en degrés)
Je viens de finir de tout rédiger au propre à l'instant, et quel plaisir de constater que nos courbes sont les mêmes ! J'avais pensé au 3dB pour la courbe réelle. Bon, heureusement d'un côté, après toutes ces explications... 
Par curiosité, avec quel logiciel peut-on obtenir ces belles courbes ? 
En tout cas, je tiens à vous remercier une nouvelle fois, je partais de très loin, et je pense avoir compris le principe général. A priori, le plus dur (pour moi) est de réussir à bien factoriser l'expression du départ pour pouvoir l'exploiter convenablement. Et l'histoire des racines positives/négatives pour des histoires de stabilité, ça, ça m'échappe encore un peu je crois...
Merci pour tout ce temps passé ! 
Les courbes sont faites avec WinEcad qui est un logiciel de simulation de circuits électroniques qui fonctionne avec Winschem.
Les courbes transitent par Photoshop pour mise à la "bonne dimension" (pas plus de 80 ko et 600 pixels) et ajout éventuel de quelques tracés.
Q est sans dimension ( ).
D'ailleurs, dans la fonction de transfert :
Il vaut mieux que Q soit sans dimension.
A priori, le plus dur (pour moi) est de réussir à bien factoriser l'expression du départ pour pouvoir l'exploiter convenablement.
Ce n'est pas toujours possible de factoriser une expression du second ordre en un produit de deux expressions du premier ordre. Cela dépend de la valeur de Q.
Sans dimension je voulais dire bien entendu désolé. L'expression de Q ne me renseigne pas beaucoup sur le fait que Q est sans dimension si ? La fonction de transfert davantage.. WinEcad "mieux" que PSpice, ou différent ? Et je n'aurai pas vraiment de "note", ou alors une qui ne compte pas pour grand chose. L'intérêt était surtout pour moi de comprendre.
Tu as raison, le plus important est de comprendre...
On va faire une analyse dimensionnelle "du pauvre"...
R est en 
L est en  .s
.s
C est en  -1.s
-1.s
donc :
Q est en ==> sans dimension
WinEcad "mieux" que PSpice, ou différent ?
Je pense que Pspice doit être mieux fini mais je ne connais pas bien Pspice. L'avantage est que WinEcad est beaucoup moins cher...
Je réponds tard, désolé. Concernant l'analyse dimensionnelle, je ne connaissais pas les "équivalences" d'unité pour la bobine et le condensateur, je ne connaissais que les bonnes vieilles unités, à savoir H et C. Comment trouve-t-on cela ?
Pour PSpice, j'utilise une version gratuite donc ça va... 
Et je finirai avec une ultime question, sans rapport direct avec l'exo, mais concernant un calcul de dB/dec. J'ai fait un tp il y a peu et j'ai obtenu la courbe ici présente ![]() . Elle représente l'évolution du rapport de la sortie sur l'entrée d'un montage à AO en fonction de la fréquence. J'avais au préalable effectué une étude théorique sur le montage, et j'avais constaté que, théoriquement, on devrait obtenir une droite à +20dB/dec jusqu'à un max. On voit bien que l'allure expérimentale est respectée. Par contre, j'ai voulu faire une comparaison des pentes et voir si l'on retrouve bien une valeur relativement proche de +20 dB/dec. Problème, la courbe que j'ai ne représente pas vraiment le gain, mais juste le rapport sortie/entrée. Ainsi, y-a-t-il un moyen pour que je puisse vérifier cette pente expérimentale ?
. Elle représente l'évolution du rapport de la sortie sur l'entrée d'un montage à AO en fonction de la fréquence. J'avais au préalable effectué une étude théorique sur le montage, et j'avais constaté que, théoriquement, on devrait obtenir une droite à +20dB/dec jusqu'à un max. On voit bien que l'allure expérimentale est respectée. Par contre, j'ai voulu faire une comparaison des pentes et voir si l'on retrouve bien une valeur relativement proche de +20 dB/dec. Problème, la courbe que j'ai ne représente pas vraiment le gain, mais juste le rapport sortie/entrée. Ainsi, y-a-t-il un moyen pour que je puisse vérifier cette pente expérimentale ?
J'espère avoir été assez clair...
Oui, bien sûr, L est en H (henry) et C en F (farad) mais on peut trouver des "équivalents" pour résoudre les équations de dimension.
On sait que . j n'intervenant pas dans la dimension, on peut écrire que
, les crochets indiquant la dimension ( [L] = dimension de L ) (je ne sais pas si cette notation est toujours en vigueur).
Donc
De même, pour C ==> .
Il y a bien sûr la "vraie" analyse dimensionnelle que tu as dû apprendre mais beaucoup plus difficile à mettre en oeuvre... Par exemple, pour la dimension de  , on a L2MT-3I-2.
, on a L2MT-3I-2.
Tout est exprimé en fonction des 4 grandeurs de base du système d'unités (SI, anciennement MKSA) :
L : longueur ==> unité : m
M : masse ==> unité : kg
T : temps ==> unité : s
I : intensité ==> unité : A
Pspice, version gratuite (ou d'évaluation) donc à performances limitées mais suffisantes sans doute pour ce que tu as à faire... La suite de logiciels WinTypon, Winschem, WinEcad permettent de faire respectivement des circuits imprimés, des schémas de circuits électroniques, des simulations de circuits électroniques à un prix très modique et 100% français, avec des liaisons entre les logiciels.
Pour trouver des dB/décade, il serait préférable d'avoir des dB. Au lieu d'avoir |Av| en ordonnée, il vaudrait mieux refaire la courbe avec 20 log(|Av|) en ordonnée.
Néanmoins, il est possible de trouver la pente sur cette courbe. Il faut prendre deux points séparés d'une décade (ou d'un nombre entier de décades) de préférence (c'est plus simple) et assez éloignés des "sommets" arrondis, par exemple :
(10000 ; 5)
(1000; 0,6)
Pour calculer la pente en dB, il faut calculer :
Donc on a +18,4 dB sur une décade donc +20 dB/décade. On ne trouve pas tout à fait 20 parce que le point 10000 est un peu trop près du "sommet" (et éventuellement les erreurs de mesure). Il faudrait prendre des points un peu plus bas en fréquence mais j'ai pris les points les plus faciles  .
.
Encore une fois, très bonne explication, très claire.
Pour l'histoire des des pentes, si par exemple je choisis deux points A et B, le premier à 1000 Hz et l'autre à 100000 Hz (donc 2 décades d'écart), il me suffira de diviser par 2, le résultat de 20log(yA/yB) n'est-ce pas ?
Oui, s'il y a 2 décades d'écart, il faudra diviser par 2 le résultat de 20 log(yB/yA) (la fréquence la plus élevée d'abord sinon on trouve l'opposé du résultat).
Plus généralement, s'il y a n décades, il faut diviser par n.
En complément, je peux te montrer ce qui se passe quand les pôles sont complexes. C'est le cas du filtre de Butterworth du 2ème ordre, par exemple.
(la fréquence la plus élevée d'abord sinon on trouve l'opposé du résultat)
Tout dépend du "sens" de la droite non ? (pente positive ou négative)
Ok pour les pôles complexes, si ça ne vous ennuie pas !
Tout dépend du "sens" de la droite non ? (pente positive ou négative)
Non, si on a +20 dB/décade par exemple, le point le plus élevé en fréquence aura une amplitude plus grande donc yB/yA > 1 ==> log(yB/yA) > 0 (ce qui donne +20 dB/décade).
Si on a -20 dB/décade, le point le plus élevé en fréquence aura une amplitude plus petite donc yB/yA < 1 ==> log(yB/yA) < 0 (ce qui donne -20 dB/décade).
Pour les pôles complexes, je mets ça demain au plus tard...
Ok 
Rien ne presse pour les pôles complexes, je suis absent à partir de demain jusqu'à dimanche soir...
Bon weekend, et encore merci !
On peut partir de l'expression d'un filtre passe-bas (pour ce qui nous intéresse, ça ne change rien).
Ou encore en posant s\,=\,j\omega :
Pour calculer les pôles, on calcule le discriminant du dénominateur :
Si :
D'où :
En multipliant par les expressions conjuguées :
Et là, c'est beaucoup moins simple parce qu'on a bien un produit d'expressions du 1er ordre au dénominateur mais, asymptotiquement, on ne sait pas faire grand-chose. Effectivement, ce n'est pas de la forme .
La seule possibilité qu'il reste est de reprendre l'expression initiale.
On calcule et on trace les courbes pour diverses valeurs de Q.
Et on obtient une série de courbes avec Q comme paramètre.
Donc c'est beaucoup moins simple lorsque les pôles ne sont pas réels. Il est beaucoup plus difficile de savoir ce qui se passe autour de . Il faut tracer la courbe.
Désolé de ne répondre que si tard, mais merci encore pour cet autre exemple ! Et en effet, l'expression trouvée paraît tout de suite moins "exploitable"... Dans quels types de circuits peut-on être amené à rencontrer un tel cas ?


