Inscription / Connexion Nouveau Sujet
FILTRE MULTIBOUCLE (niveau: bts systémes électroniques)
Voici mon énoncé:
1-exprimer la transmittance T=Vs/Ve en fonction de R1,R2,R3,C1,C2,w
(w=oméga)
2-mettre T sous la forme suivante:
T=T0.(1+jf/f1)/(1+jf/f2)(1+jf/f3)
on précisera les expressions littérales de T0,f1,f2,f3
3-montrer que cette expression de T est le produit d'une constante et de fonctions élémentaires du 1er ordre dont on tracera séparément le diagramme de bode asymptotique.
4- en utilisant les résultats de la question précédentes tracer le diagramme de bode asymptotique et réel de T
5- quelle est la nature du filtre étudié? quelle est sa transmittance maximale?
J'ai réussi a répondre aux 1 et 2, voici mes résultats:
1-T= -R2/R3.(1+jwc1(r1+r3))/(1+jr1c1w)(1+jr2c2w)
2- en fonction de la fréquance cela donne
T(jf)= -R2/R3.(1+j2
fc1(r1+r3))/(1+jr1c1.2f)(1+jr2c2.2f)
donc T0= -R2/R3
f1=1/2c1(r1+r3)
f2=1/2r1c1
f3=1/2r2c2
et je bloque sur les questions 3, 4 et 5
quelqu'un pourrai m'aider je ne m'en sort vraiment pas! merci d'avance
T est le produit d'une constante par les fonctions élémentaires du 1er ordre
,
,
Tracer le diagramme de Bode asymptotique de ces trois les fonctions du 1er ordre, tu sais faire ?
ok merci! je voulais vous demandé aussi pour
1/1+jf/f2 et 1/1+jf/f3
j'ai trouvé un gain G(f)=-10log(1+(f/f2)²)^-1/2
pour le tracé asymptotique jai donc procédé comme cela:
en BF f<<f2
alors(f/f2) tends vers 0 donc négligeable devant 1
donc G(f)=-10log(1)=0dB
en HF f>>f2
alors(f/f2) tends vers l'infini donc 1 est négligeable devant (f/f2)²
donc G(f)= -10 log(f/f2)²
= -10(log f² - log f2²)
G(f) = -20 log f + 20 log f2
on effectue un changement de variable, on pose X= log f
et 20 log f2 est une constante
donc G(f)=-20X + K
et on procéde de la même maniére pour 1/1+jf/f3
mon raisonement est il bon?
Le raisonnement est tout à fait exact.
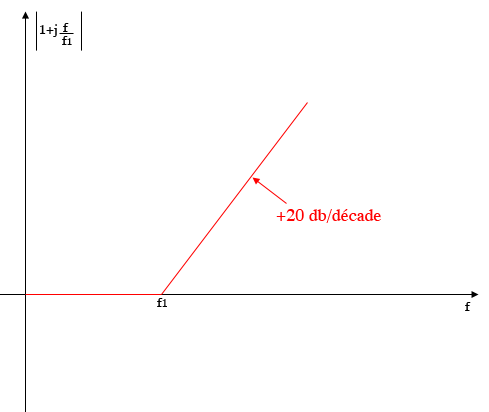
Pour f2 et f3, on obtient une courbe comme pour f1 à part qu'elle est vers le bas à -20 dB/décade.
On demande le "diagramme de Bode"... Il n'est pas précisé "seulement l'amplitude" donc, à mon avis, il faut faire la phase aussi.
oui oui il faut faire aussi la phase! aprés je sais faire le reste je n'étais pas certain de mon raisonnement mais vous me l'avez confirmé! merci encore marc et bonne soirée!
Annuler
connectez vous