Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... IutForum Supérieur (IUT) PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau iut
Partager :

Filtre en T

Posté par Profil philou28 05-09-16 à 23:08

Bonjour

Impossible de faire la fonction de transfert depuis 3 heures....

Merci pour l'aide

Filtre en T

Posté par
vanoisere : Filtre en T 06-09-16 à 12:26

Bonjour
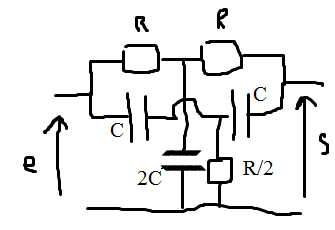
C'est vrai que si tu utilises la loi des nœuds et des mailles... Connais-tu le théorème de Millman ?

Posté par Profil philou28re : Filtre en T 06-09-16 à 12:37

oui mais je n'arrive pas à l'appliquer ici

Posté par
vanoisere : Filtre en T 06-09-16 à 14:10

Je pose : G=\frac{1}{R} et x=R.C.\omega ; le potentiel du nœud commun aux deux résistances R s'écrit :

V_{1}=\frac{G.e+G.s}{2G+2jC.\omega}=\frac{e+s}{2\left(1+j.x\right)}
Le potentiel du nœud commun aux deux capacités C s'écrit :

V_{2}=\frac{jC.\omega.\left(e+s\right)}{2jC.\omega+\frac{2}{R}}=\frac{jx}{2\left(1+j.x\right)}\left(e+s\right)
Théorème de Millman appliqué à la sortie :

s=\frac{G.V_{1}+jC.\omega.V_{2}}{G+jC.\omega}=\frac{V_{1}+j.x.V_{2}}{1+j.x}
En remplaçant V1 et V2 par leurs expressions dans l'expression de s, on obtient :

2s\left(1+j.x\right)^{2}=\left(e+s\right)\left(1-x^{2}\right)
D'où la fonction de transfert :

\underline{H}=\frac{s}{e}=\frac{1-x^{2}}{1+4j.x-x^{2}}
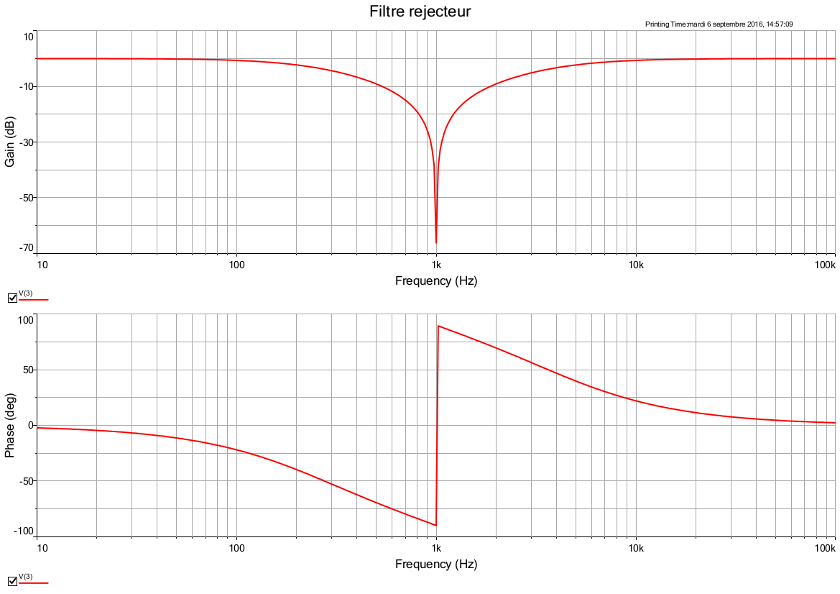
Je te laisse ” arranger ” l'expression en fonction de tes habitudes. On obtient un filtre réjecteur, appelé aussi filtre coupe-bande.

Posté par
vanoisere : Filtre en T 06-09-16 à 14:22

Petit problème de l'éditeur d'équation dans mon expression de V2 :

V_{2}=\frac{jC.\omega.\left(e+s\right)}{2jC.\omega+\frac{2}{R}}=\frac{jx}{2\left(1+j.x\right)}\left(e+s\right)

Posté par Profil philou28re : Filtre en T 06-09-16 à 14:48

Merci

Peux tu m'expliquer comment tu calcules V1 ?

Posté par
vanoisere : Filtre en T 06-09-16 à 15:14

Si cela peut t'aider, voici le diagramme de Bode tracé pour :

R.C=\frac{1}{\omega_{0}}=\frac{1}{2\pi.f_{0}}\quad avec\quad f_{0}=1,0kHz

Filtre en T

Posté par
vanoisere : Filtre en T 06-09-16 à 15:30

Citation :
Peux tu m'expliquer comment tu calcules V1 ?

Les trois expressions de potentiels que j'ai écrites sont trois applications directes du théorème de Millman. Si tu as un problème avec ce théorème, tu peux étudier la fiche que j'ai élaborée sur le sujet ici : (fiche n° 1).
Si cela te pose toujours problème, pose de nouvelles questions sur ce forum.

Posté par
vanoisere : Filtre en T 06-09-16 à 15:36

Au cas où il ne s'agirait que d'un problème de calculs, voici le détail :

V_{1}=\frac{\frac{e}{R}+\frac{s}{R}}{\frac{2}{R}+2jC.\omega}
En multipliant tous les termes par R :

V_{1}=\frac{e+s}{2+2j.R.C.\omega}=\frac{e+s}{2\left(1+j.x\right)}


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !