Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieurForum supérieur ingé PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau école ingénieur
Partager :

Filtre double T à amortissement parallèle

Posté par
futzakepf 03-06-16 à 17:00

Bonjour,

Je suis nouveau sur ce site.

Je n'arrive pas à faire un exercice sur le filtre double T à amortissement parallèle.
La question est de montrer que la fonction de transfert (Vs/Ve) est minimale quand la fréquence centrale f = (1+a)/(2*pi*RC) et elle vaut alors R/2Rp.

Je pense qu'il faut utiliser le théorème de Millmann aux noeuds A, B et S, puis en déduire le rapport Vs/Ve et faire l'étude de la fonction en fonction de w. Le problème est que je n'arrive pas à aboutir dans mes calculs, lorsque j'injecte Va et Vb dans l'expression de Vs.

Je vous envoie une photo du montage.

Merci d'avance.

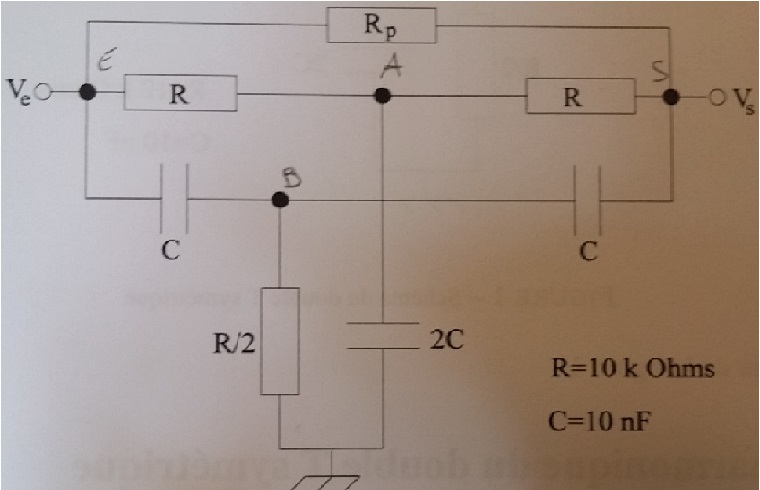
Filtre double T à amortissement parallèle

Posté par
futzakepfre : Filtre double T à amortissement parallèle 03-06-16 à 17:02

Je vous envoie mes débuts de calculs.

** image supprimée **

***Edit gbm : les énoncés et les propositions doivent être tapées, non scannée (sauf pour les images et schémas)

Posté par
vanoisere : Filtre double T à amortissement parallèle 03-06-16 à 17:39

Bonjour
Le plus simple (si on peut dire car le calcul est tout de même un peu long) consiste à mon avis à utiliser trois fois le théorème de Millman . J'obtiens tes trois expressions que je simplifie en posant x = RCw.

V_{A}=\frac{V_{e}+V_{s}}{2\left(1+jx\right)}\quad;\quad V_{B}=\frac{jxV_{e}+jxV_{s}}{2\left(1+jx\right)}

V_{s}=\frac{R_{p}V_{A}+jR_{p}xV_{B}+RV_{e}}{R+R_{p}+jR_{p}x}

\left(R+R_{p}+jR_{p}x\right)V_{s}=\frac{R_{p}\left(V_{e}+V_{s}\right)-x^{2}R_{p}\left(V_{e}+V_{s}\right)+2R\left(1+jx\right)V_{e}}{2\left(1+jx\right)}

2\left(1+jx\right)\left(R+R_{p}+jR_{p}x\right)V_{s}=R_{p}\left(V_{e}+V_{s}\right)-x^{2}R_{p}\left(V_{e}+V_{s}\right)+2R\left(1+jx\right)V_{e}

Tu n'as plus qu'à regrouper les termes dépendant respectivement de Ve et de Vs...

Posté par
vanoisere : Filtre double T à amortissement parallèle 03-06-16 à 17:58

Sauf erreur ou étourderie :

\underline{H}=\frac{2R+R_{p}\left(1-x^{2}\right)+2jxR}{2R+R_{p}\left(1-x^{2}\right)+2jx\left(2R_{p}+R\right)}

Posté par
futzakepfre : Filtre double T à amortissement parallèle 03-06-16 à 18:02

Merci

Posté par
futzakepfre : Filtre double T à amortissement parallèle 03-06-16 à 18:06

Impeccable, je trouve la même fonction de transfert en suivant cette méthode.

Merci pour votre aide.

Posté par
vanoisere : Filtre double T à amortissement parallèle 04-06-16 à 00:06

J'espère que tu es très à l'aise en math car la suite est très calculatoire. Devant m'absenter tout le week end, je te laisse le résultat : à toi de le retrouver.
En étudiant la dérivée du module de H en fonction de x = RCw, on montre que ce module passe par un minimum pour une valeur xo :

x_{0}=2\pi RCf_{0}=\sqrt{\frac{R_{p}+2R}{R_{p}}}

Si on suppose Rp>>R on peut effectuer un développement limité à l'ordre 1 en R/Rp :

x_{0}=2\pi RCf_{0}=\left(1+\frac{2R}{R_{p}}\right)^{\frac{1}{2}}\approx1+\frac{R}{R_{p}}

La valeur minimale du module de H est alors :

H_{min}=\frac{R}{2R_{p}+R}

En supposant encore Rp>>R :

H_{min}\approx\frac{R}{2R_{p}}

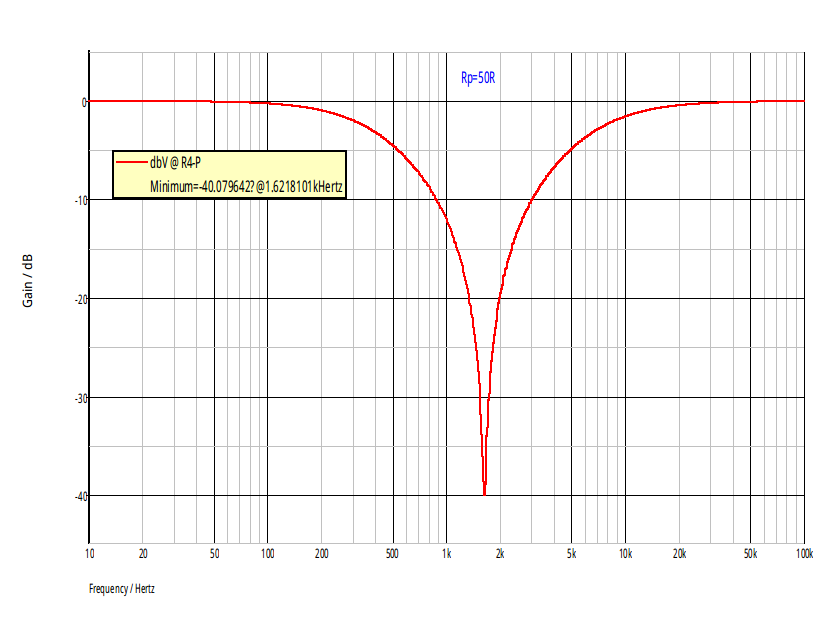
On comprends bien physiquement que plus Rp est grand devant R, plus l'intensité du courant dans Rp devient faible, plus l'influence de Rp diminue, plus le comportement du filtre se rapproche de celui du réjecteur (ou coupe-bande) classique. On peut vérifier que l'on obtient bien la fonction de transfert du réjecteur classique en faisant tendre Rp vers l'infini dans l'expression obtenue ici. Pour illustrer cela, je joins ci-dessous les diagrammes de Bode du gain pour Rp=R puis Rp=50R.

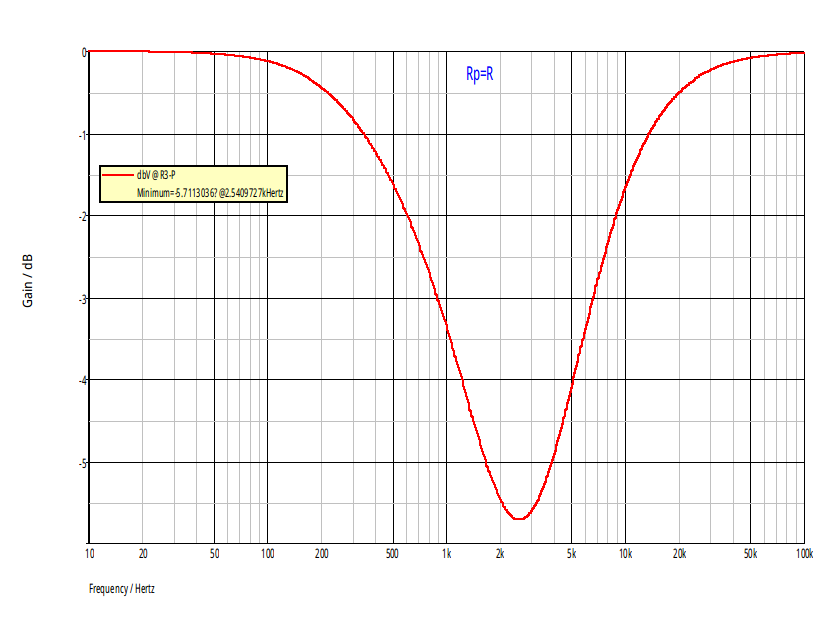
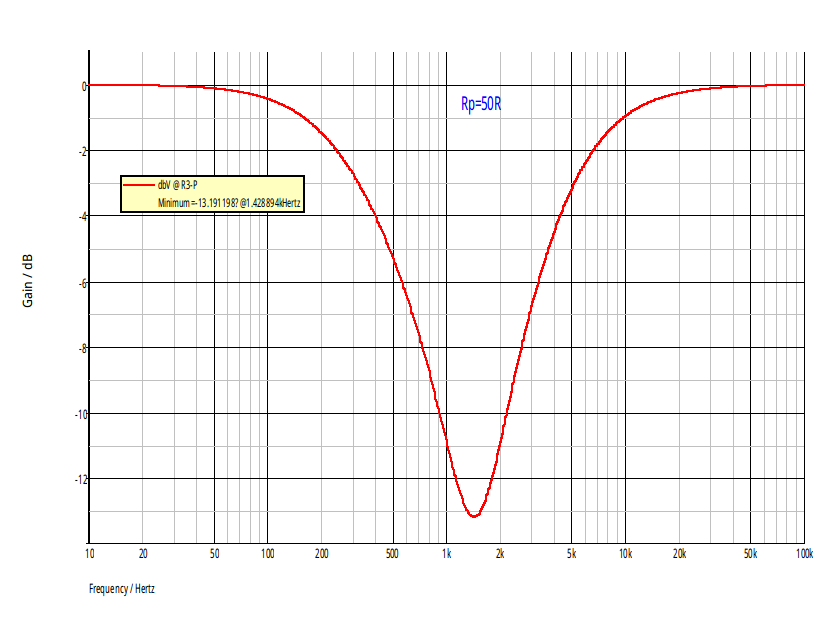
Filtre double T à amortissement parallèle

Filtre double T à amortissement parallèle

Posté par
vanoisere : Filtre double T à amortissement parallèle 04-06-16 à 10:44

Bonjour
Je viens de constater que les coordonnées du minimum de gain ne correspondent pas sur mes simulations au valeurs théoriques : étourderie de ma part : j'avais choisi comme résistance reliée à la masse 2R au lieu de R/2. Voici les deux diagrammes de Bode corrects.

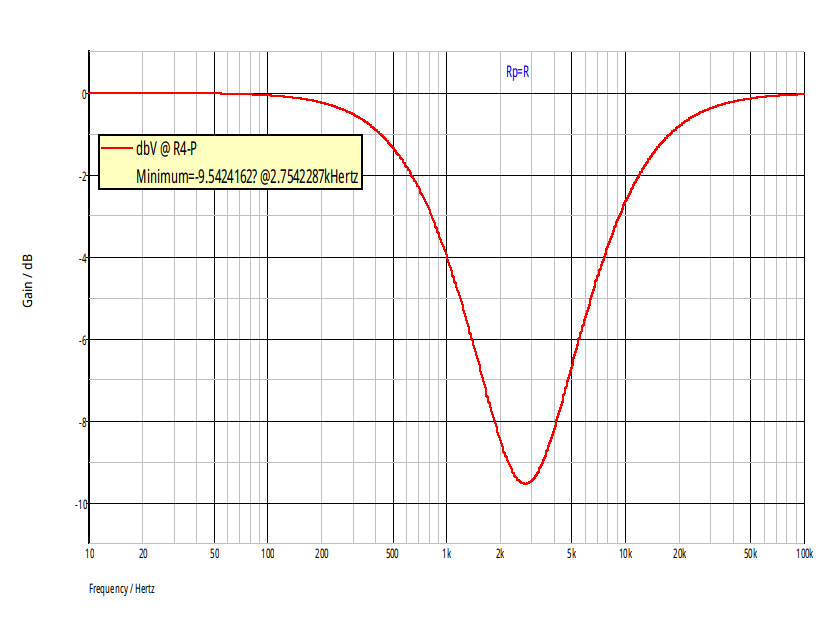
Filtre double T à amortissement parallèle

Filtre double T à amortissement parallèle

Posté par
futzakepfre : Filtre double T à amortissement parallèle 06-06-16 à 18:39

Bonjour,
Merci pour tout ceci, serait-il possible d'avoir le module de H et la dérivée associée pour pouvoir avoir des checkpoints car c'est vrai que c'est hyper calculatoire et me lancer dans le flou comme ça c'est pas mon fort.

Encore merci !!

Posté par
vanoisere : Filtre double T à amortissement parallèle 06-06-16 à 19:38

Bonjour
Le module de H étant strictement positif, son tableau de variation en fonction de x est le même que celui de son carré :

H^{2}=\frac{\left[2R+R_{p}\left(1-x^{2}\right)\right]^{2}+4R^{2}x^{2}}{\left[2R+R_{p}\left(1-x^{2}\right)\right]^{2}+4x^{2}\left(2R_{p}+R\right)^{2}}
La dérivée par rapport à x admet comme numérateur :

Y=32xR_{p}\left[x^{4}\left(Rp^{3}+RR_{p}^{2}\right)-4R^{3}-8R^{2}R_{p}-5RR_{p}^{2}-R_{p}^{3}\right]
Le dénominateur de la dérivée est évidemment strictement positif ; inutile de l'expliciter. L'étude de Y montre que le module de H admet un minimum pour une valeur de x :

x_{0}=RC\omega_{0}=\sqrt[4]{\frac{4R^{3}+8R^{2}R_{p}+5RR_{p}^{2}+R_{p}^{3}}{R_{p}^{3}+RR_{p}^{2}}}=\sqrt{\frac{2R+R_{p}}{R_{p}}}
Il ” suffit ” ensuite de reporter cette valeur de xo dans l'expression du carré de H pour obtenir l'expression du module de H....


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !