Niveau licence

Filtre avec AOP

Posté par
Jean469 20-01-16 à 16:24

Bonsoir,j'ai tenté de faire cet exercice mais un coup de main est bienvenue(schéma en bas):
j'ai répondu à la question 1  déja,ma réponse est bonne,le gain maximum est 1/2 et c'est un filtre passe bande,ce que j'ai écrit est valable seulement pour un AOP idéal
voici les questions:

1 ) Calculer  Vs / Ve comme 1 / (A + JB).
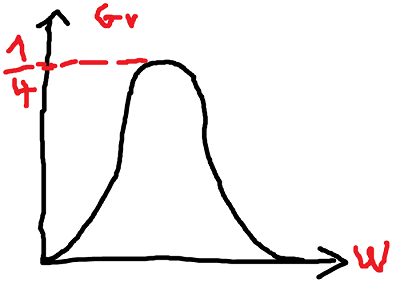
2 ) par l'étude de la trace |vs/ve| déduire la nature du filtre.
3 ) Estimer pour phi w -> 0 et  l'infini
En déduire w valeur pour lesquelles Vs ( t) et Ve (t ) sont en phase .
Quel est l'intérêt du filtre avec AOP?

Pour la question 1)
j'ai dit z=...et z'=...(voir schéma);Ve=z.ie et Vs=z'ie.
Donc $vs/ve=(rjcw)/(1+rjcw)^2=rjcw/(1-r^2.c^2.w^2+2rjcw)=1/(-j/rcw+jrcw+2)$
Le gain max étant $1/2$ ,le tracé obtenue est en bas.

Sinon on me demande dans la question 3) d'estimer $\phi$ pour $w->0$ et l'infini.
Je suppose qu'il demande le déphasage de |vs/ve| mais pour les deux limite,Gv=0 et on sait que $\phi= \phi_u- \phi_i=arg(z)=arctg(0/0)$ vu que $vs/ve=0$ pour les 2 limites.

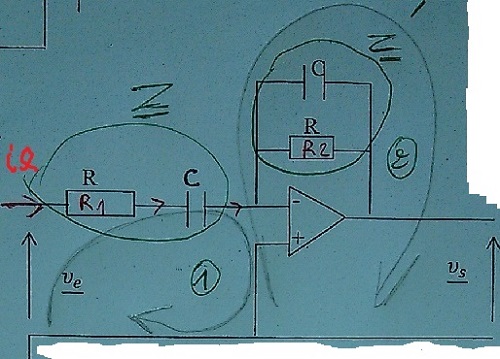
Filtre avec AOP

Posté par re : Filtre avec AOP 20-01-16 à 18:01

Pour les questions "qualitatives" du début, il faut remarquer :
$Z_{C}=\frac{1}{C\omega}\quad;\quad\lim_{\omega\rightarrow0}\left(Z_{C}\right)=\infty\quad;\quad\lim_{\omega\rightarrow\infty}\left(Z_{C}\right)=0$
A très haute fréquence, le condensateur se comporte comme un fil d'impédance nulle (ou un interrupteur fermé) ; à très basse fréquence, il se comporte comme un interrupteur ouvert. Cela permet d'obtenir les schémas équivalents du circuit à très basse puis à très haute fréquence et de répondre aux trois premières questions...

Posté par re : Filtre avec AOP 20-01-16 à 19:33

Je suppose : R1=R2 = R. Pour les déphasages en particulier mais aussi pour la suite des calculs, tu as tout intérêt à faire en sorte que le numérateur soit un réel. On obtient , me semble-t-il, quelque chose de ce genre :

$\boxed{\underline{H}=\frac{\underline{v_{s}}}{\underline{v_{e}}}=\frac{-\frac{1}{2}}{1+\frac{j}{2}\left(RC\omega-\frac{1}{RC\omega}\right)}}$
A haute fréquence :

$RC\omega\gg1\gg\frac{1}{RC\omega}$
A basse fréquence :

$RC\omega\ll1\ll\frac{1}{RC\omega}$
Remarque :
Basse fréquence signifie rigoureusement : <<1/(RC)
Haute fréquence signifie rigoureusement : >>1/(RC)

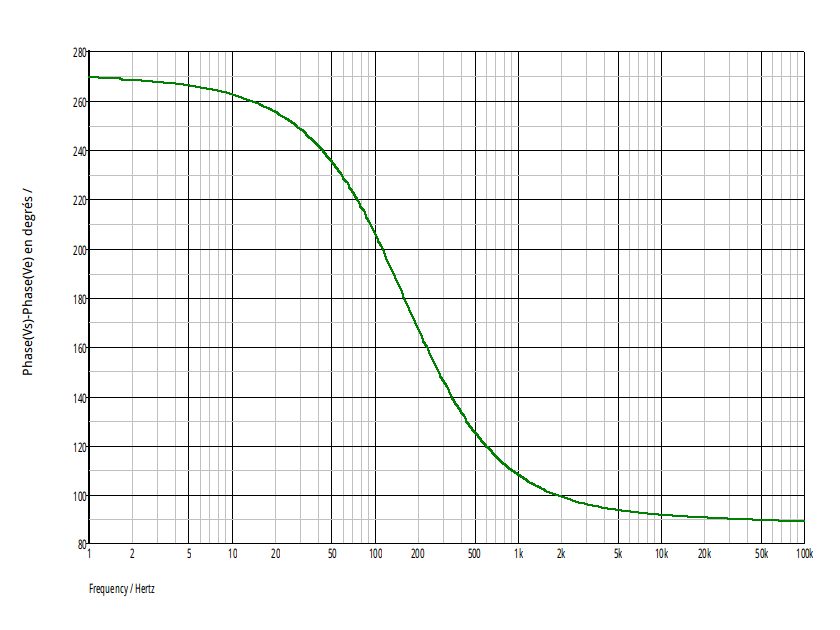
Posté par re : Filtre avec AOP 20-01-16 à 23:22

J'espère que cela va t'aider : voici la courbe représentant les variations du déphasage en fonction de la fréquence (échelle logarithmique pour la fréquence) pour f compris entre 1Hz et 100kHz.
J'ai choisi : RC = 10^-3s.

Filtre avec AOP

Posté par re : Filtre avec AOP 21-01-16 à 12:37

Bonjour,oui ça m'aidera sans aucun doute,je vais regarder cela de manière plus approfondi plus tard,en tous cas merci .

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Filtre avec AOP

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique