Inscription / Connexion Nouveau Sujet
filtre adsl
Bonjour,
J'ai un tp à préparer pour la semaine prochaine et j'ai quelques petites questions.
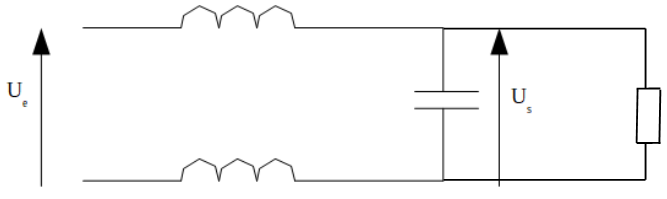
On étudie un filtre LCL série avec us la tension aux bornes de C (cf image jointe).
On a L=11mH pour chaque bobine et C=30nF
Voici ce qu'on me dit :
On branche sur ce filtre un téléphone d'impédence d'entrée de l'ordre de 600
.
1) En utilisant des schémas équivalents, prévoir les comportements du filtre à basse fréquence et à haute fréquence.
2) Etudier expérimentalement le comportement du filtre ADSL avec une résistance de 600 branchée en sortie simulant le téléphone. Donner les résultats expérimentaux et commenter.
3) Déterminer expérimentalement la fréquence de coupure du montage. Commenter par rapport à l'intérêt d'un tel filtre.
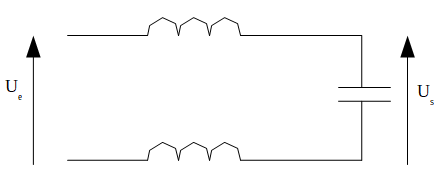
Tout d'abord j'aimerais juste savoir si j'ai branché la résistance représentant le téléphone au bon endroit (cf 2e image jointe).
Ensuite j'ai une question sur le filtre LCL uniquement : quand j'avais étudié ce filtre j'avais trouvé sachant que la fonction de transfert s'écrivait sous la forme
et le professeur avait écrit sur ma copie que c'était faux mais comme je n'ai pas eu la correction je ne comprends pas pourquoi. Est-ce qu'on peut m'expliquer s'il-vous-plaît ?
Merci d'avance pour vos explications !
Bonjour
Le montage me semble correct. Le branchement de la charge modifie le fonctionnement du filtre puisque la fonction de transfert d'un filtre est calculée à courant de sortie d'intensité nulle.
Pour l'autre question , avec A et B réels :
si : , on obtient :
seulement si A est un réel positif ; sinon, il faut introduire un décalage supplémentaire de 
rad.
J'ai eu l'occasion d'expliquer cela en détail il y a quelque temps sur ce forum, messages du 31-03-18 à 15:27 et suivants :
Filtre Actif 2ème ordre
1. J'ai fait une étude asymptotique du circuit à basse fréquence et à haute fréquence comme indiqué dans la 1ere question. A basse fréquence, je trouve un gain qui vaut 1 et à haute fréquence je trouve un gain qui vaut 0. Est-ce que c'est bien cela ? Dans ce cas cela signifierait que le comportement du filtre LCL n'est pas modifié et que le filtre est toujours un passe-bas.
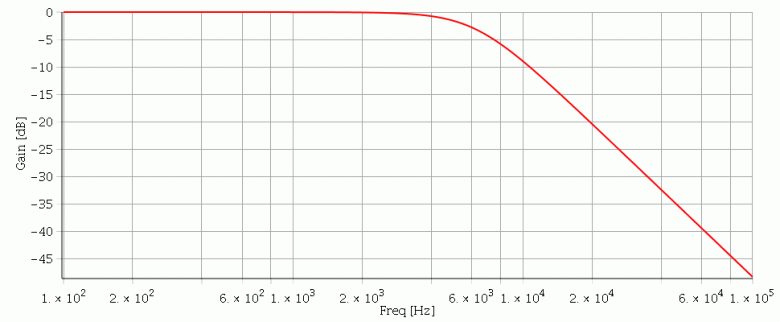
2. J'ai l'impression que le graph du gain que tu me donnes confirme le résultat de la question 1. Est-ce que c'est le cas ?
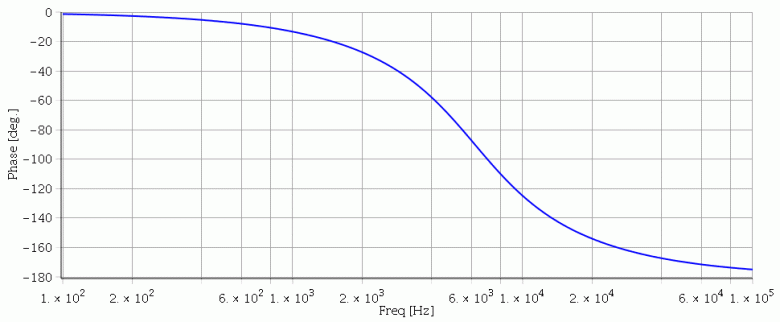
Pour le déphasage : du coup pour le circuit LCL (sans le téléphone) on a :
-si f<fo alors
-si f>fo alors
Est-ce que c'est ça ?
Après de manière pratique j'ai un peu de mal à analyser le graphique que tu me donnes vis-à-vis de ce résultat
13. Pour déterminer la fréquence de coupure du montage ce serait plus facile si on connaissait déjà le gain maximal. Est-ce que c'est le même que pour le circuit LCL ?
Tu as effectivement un filtre passe-bas et la présence ou non de R en sortie ne modifie pas la nature du filtre.
Le diagramme de Bode correspond à un filtre passe-bas du second ordre. Ici le Gain maximum vaut zéro et la phase vaut zéro. Pour les fréquences nettement supérieures à la fréquence propre, la courbe du gain est assimilable à une oblique de pente -40dB/décade. La phase tend vers -180° à haute fréquence.
OK pour tes expressions de la phase. Pour interpréter, si tu n'es pas très à l'aise avec la fonction arctangente, n'oublie pas :
Pour déterminer la fréquence de coupure fc si tu disposes du diagramme de Bode expérimental : rechercher la fréquence pour laquelle :
GdB=(Gmax -3)dB
Sur le plan théorique, cette fréquence de coupure correspond à :
Ok merci
Je ne savais pas que expérimentalement on trouvait la fréquence de coupure en faisant GdB=(Gmax - 3)dB
Par contre je connais la formule Gc=Gmax/
2
Est-ce qu'il y a un lien entre les deux ?
On voit bien sur le diagramme de Bode du gain que la fréquence de coupure est un peu supérieure à 6kHz. L'étude théorique avec les valeurs de R, L et C que tu as indiquées conduit à fc
6,14kHz.
Annuler
connectez vous