Inscription / Connexion Nouveau Sujet
Filtre
Bonsoir ! alors voila comme je n'ai pas encore touchés ce type de filtre alors j'ai quelque problème à le faire :
1. Determiner la fonction de transfert du filtre complet. La mettre sous forme
canonique.
J'ai un peu de mal, faut-il déterminer l'impédance équivalente entre le filtre 1 et 2 ? si oui j'ai : (Zc(Zc+R))/(Zc2*R)
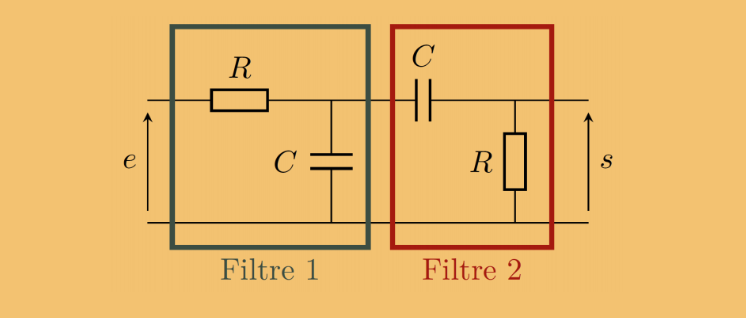
2. Determiner la fonction de transfert pour les deux filtres pris en sortie ouverte
(notes Filtre 1 et Filtre 2 sur la figure). Preciser la nature de chacun des filtres
en etudiant les limites asymptotiques. Determiner le produit des fonctions de
transfert en circuit ouvert. La mettre sous forme canonique.
Celle la pas de problème le filtre 1 est un passe-bas du premier ordre et le filtre 2 un passe-haut du premier ordre
3. Comparer les deux fonctions de transfert (obtenues en Q1 et en Q2) en circuit
ouvert. Preciser dans chacun des cas la nature du filtre obtenu.
J'ai besoin de la Q.1 mais comme j'ai pas réussi à trouver s/e .. ça m'avancera pas à grande chose
Bonsoir
Comme tu l'as écrit, le filtre 1 est un passe-bas du premier ordre. Le filtre 2 est un passe-faut du premier ordre.
En associant les deux en cascade, tu dois logiquement obtenir un passe-bande dont tu connais surement l'expression canonique de la fonction de transfert.
Si tu ne connais pas le théorème de Milman, tu peux assez facilement obtenir cette fonction de transfert de la façon suivante :
1° : calculer l'impédance équivalente de l'association série (RC du filtre 2) : il s'agit bien d'une association série puisque la sortie du filtre 2 est ouverte.
2 ° calculer alors l'impédance équivalente Ze à l'association en parallèle du (RC) précédent avec le C du premier filtre.
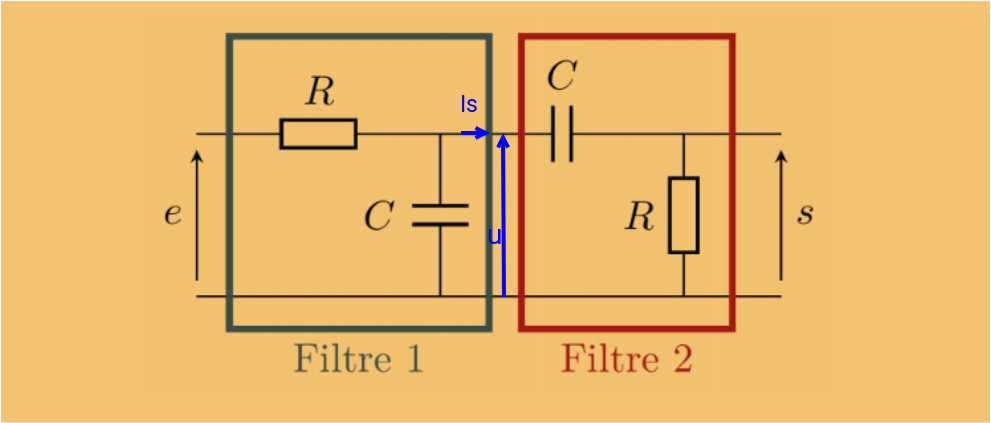
3° L'association série du R du premier filtre et de Ze se comporte en diviseur de tension vis à vis de la tension d'entrée e. Cela te permet d'obtenir la tension u correspondant à la sortie du filtre 1 et à l'entrée du filtre 2 ; tension que tu aurait directement obtenu à l'aide du théorème de Milman.
4° L'association série RC du filtre 2 se comporte en diviseur de tension vis à vis de cette tension u.
Pour la Q.2 j'obtiens pas vraiment un passe-bande, avec le filtre 1 j'ai 1/(jx+1) et avec le filtre 2 j'ai : (jx)/(1+jx) avec Wo=1/RC et x=W/Wo
en fesant le produit des deux je ne vois pas comment faire intervenir le facteur de qualité Q
j'obtiens : (jx)/(-x2+2jx+1)
Je ne suis pas sûr que tu ais compris le but de l'exercice...
Une fonction de transfert se détermine par convention en circuit ouvert (intensité du courant de sortie nulle)
Pour Q2 : La fonction de transfert H1 du filtre 1 en supposant l'intensité du courant de sortie de ce filtre 1 est celle d'un passe-bas du premier ordre : celle que tu obtiens.
La fonction de transfert du filtre 2 supposé seul avec aucun courant de sortie est celle d'un passe-haut du premier ordre : celle que tu obtiens. Tout cela a été expliqué dans mon premier message.
Si maintenant tu calcules le produit H1.H2, tu vas obtenir la fonction de transfert d'un passe-bande.
Cependant, ce produit H1.H2 ne représente pas la fonction de transfert du filtre complet H que tu dois obtenir à la première question par la méthode que je t'ai indiquée ou par utilisation du théorème de Milman. En effet, dans l'association des deux filtres, le courant de sortie du filtre 1 n'est pas nul comme cela a été posé pour calculer H1.
Bah enfaite que l'intensité du courant soit nulle ou non je ne vois pas qu'est-ce que cela va changer dans mon expression, et quand vous m'avez expliqué comment procéder c'est encore un peu flou pour moi, l'impédance équivalente se calcul entre le Zc du filtre 1 et R du filtre 2 ? du coup je touche pas au Zc du filtre 2 ?
Bon c'est un peu étrange mais j'ai trouvé Zeq=
Après avoir fait les calculs je tombe sur :
Je pense avoir fait une erreur ..
Je reprends la fin de mon message précédent avant de répondre à ton dernier message.
Tes expressions de H1 et de H2 sont correctes et le produit des deux correspond bien à ce que tu as écrit :
En divisant tous les termes par 2jx, cela donne :
Cela correspond bien à une fonction de transfert d'un passe bande donc la forme canonique est :
Pour la fonction de transfert H du filtre demandé en Q1, l'expression que tu obtiens est celle de où u désigne la tension qui est à la fois la tension de sortie du filtre 1 et la tension d'entrée du filtre 2 :
Pour avoir la fonction de transfert , il faut considérer que l'ensemble (RC) du filtre 2 se comporte en diviseur de tension :
Cela donne au final :
Comme déjà expliqué :
Ah bah oui ça colle, mais c'etait vraiment pas intentionnelle, je savais meme pas que j'avais calculé s/u, du coup meme quand vous dites que
u désigne la tension qui est à la fois la tension de sortie du filtre 1 et la tension d'entrée du filtre 2
Le schéma complété devrait t'aider.
J'insiste, l'expression de H1 que tu as obtenu suppose Is=0, ce qui n'est pas le cas lorsque le filtre 2 est associé au filtre 1. C'est pour cette raison que la fonction de transfert H de l'association n'est pas égale au produit H1.H2.