Niveau maths spé

Filtrage linéaire

Posté par
superjuju45 10-09-19 à 12:12

Bonjour, je bloque sur l'exercice suivant :

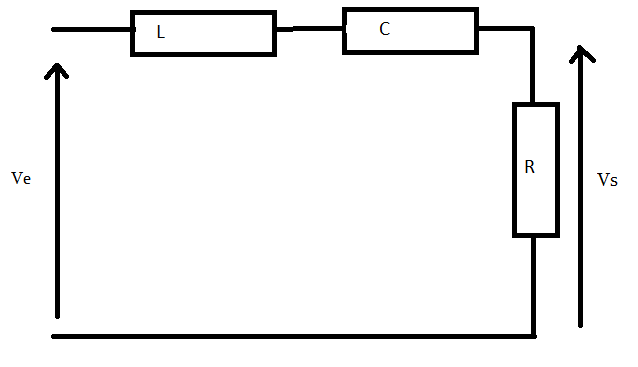
On injecte dans le circuit ci-dessous de pulsation propre ₀ le signal V_e(t)=2Acos(100₀t)cos(101₀t).

a) Déterminer le signal de sortie aux bornes de la résistance.
b) On alimente le circuit par un signal triangulaire. Donner l'allure de la tension de sortie en fonction de .

Je bloque à la question a) :

J'ai déterminé la fonction de transfert du circuit : un filtre passe-bande du second-ordre avec H₀=1, Q= $\frac{1}{R}\sqrt{\frac{L}{C}}$ et ₀= $\frac{1}{\sqrt{LC}}$

Ensuite comme H=V_s/V_e
V_s=HV_e
et en multipliant en haut en et en bas par $1-jQ(\frac{\omega }{\omega _{0}{}}-\frac{\omega _{0}}{\omega })}$

et je trouve : V_s= (V_e- $\frac{Q}{\omega _{0}}$ jV_e-Q₀ $\frac{1}{j\omega }$ V_e) $\times \frac{1}{1+Q²(\frac{\omega }{\omega _{0}}-\frac{\omega _{0}}{\omega })}$
mais je suis embêté par les au dénominateur.

Filtrage linéaire

Posté par re : Filtrage linéaire 10-09-19 à 14:42

Bonjour
C'est vrai qu'en cours de mathématiques, on apprend à presque toujours obtenir le résultat en multipliant le dénominateur d'un complexe par son conjugué. Cette méthode est rarement la meilleure en physique. Ici, très simplement :

$\underline{H}=\frac{H_{o}}{1+jQ\left(\frac{\omega}{\omega_{o}}-\frac{\omega_{o}}{\omega}\right)}\quad;\quad H=\frac{H_{o}}{\sqrt{1+Q^{2}\left(\frac{\omega}{\omega_{o}}-\frac{\omega_{o}}{\omega}\right)^{2}}}$

puisque, ici, H_o > 0.

Pour la suite, il peut être intéressant de transformer le produit de deux cosinus par une somme de deux cosinus. Un des termes est de pulsation _o, l'autre est de pulsation très supérieure à _o ; tu sais également comment se comporte le filtre vis à vis d'un tel signal...

Posté par re : Filtrage linéaire 10-09-19 à 20:25

Avec tes indications je trouve :
V_s= $\frac{Acos(201\omega _{0}t)+Acos (\omega _{0}t)}{\sqrt{1+Q²(\frac{\omega }{\omega _{0}}-\frac{\omega _{0}}{\omega })²}}$ mais ça ne pose pas de problème d'avoir des au dénominateur alors que la nouvelle variable est t ?

Posté par re : Filtrage linéaire 10-09-19 à 23:06

Puisque la tension d'entrée est la somme de deux tensions sinusoïdales :

$v_{e}=v_{e1}+v_{e2}$

La linéarité du système permet d'écrire la tension de sortie comme une somme de deux tensions sinusoïdales :

$v_{s}=v_{s1}+v_{s2}$

Tu obtiens v_s1 en étudiant l'influence du filtre sur la tension v_e1. Pour cette tension, la situation est particulièrement simple puisque la pulsation est la pulsation propre :

$\\ \omega_{1}=\omega_{o}\quad;\quad\underline{H}=H_{o}=1\quad donc\quad v_{s1}=v_{e1}$

v_s2 est la tension de sortie du filtre dans le cas particulier où la tension d'entrée serait v_e2 :

$\omega_{2}=201\omega_{0}\quad v_{s2}=H.A.\cos\left(201\omega_{o}.t+\varphi\right)$

avec :

$H=\frac{H_{o}}{\sqrt{1+Q^{2}\left(201-\frac{1}{201}\right)^{2}}}\quad;\quad\varphi=\arg\left[1-jQ\left(201-\frac{1}{201}\right)\right]$

J'ignore la valeur de Q. Si cette valeur est assez importante, (filtre passe bande très sélectif) v_s2 est alors totalement négligeable :

$v_{s}\approx v_{s1}$ ???

Cela illustrerait bien les propriétés d'un filtre passe bande très sélectif : il conserve les tensions de fréquences très proches de la fréquence propre (fréquence de résonance) et élimine les tensions de fréquences hors de la bande passante.