Inscription / Connexion Nouveau Sujet
Filtrage linéaire
Bonsoir ! Je bloque énormément sur ce chapitre !
On souhaite réaliser un moyennateur pour un signal de fréquence fe=300Hz. On envisage deux filtres passe-bas de meme pulsation de coupure w0=628rad/s et de fonction de transfert :
H1(jw)= et H2(jw)=
1) vérifier que w0 est bien la pulsation de coupure à -3dB de chacun des deux filtres
2) Le signal d'entrée est : e(t)=E0(1+cost(2
fet)) avec E0=2. Exprimer le signal de sortie pour les deux filtres. Quel est le meilleur moyennateur
Voila. Je n'ai vraiment pas d'idée solide de ce que je dois faire, est-ce que c'est une étude amplitude et de phase puis un tableau de variations ? ou bien je peux calculer omega directement avec la fréquence fe et montrer que le rapport de w/w0=1 ?
Merci de me donner des pistes s'il vous plait !
Bonsoir
Le signal dont tu cherches à obtenir la valeur moyenne en sortie a pour fréquence :
fe=3fo.
En dehors de la bande passante, le diagramme de Bode du gain est assimilable à une droite de pente -20dB/décade pour le filtre du premier ordre et à une droite de pente -40dB/décade pour le filtre du deuxième ordre. Tu as donc intérêt à choisir le passe-bas du deuxième ordre : c'est lui qui va le plus atténuer les composantes (ou la composante) sinusoïdale(s) du signal en conservant la composante continue qui est égale à la valeur moyenne.
Le signal dont tu cherches à obtenir la valeur moyenne en sortie a pour fréquence :
fe=3fo.
ça ne résoud pas mon problème puisque si omega est la pulsation de coupure alors je devrais pouvoir l'observer sur le diagramme de bode juste avant la pente de -20dB
Tu dois bien connaître tout de même la relation entre pulsation et fréquence !
Pour la suite, si tu n'es pas convaincu, calcule le module de H pour w=3wo. Tu verras bien lequel des deux filtres atténue le plus !
AHHH MINCE bah enfaite je l'avais fais dans ma tete ce calcul mais JE PENSAIS que c'etait égal à 300 tout comme f0 .. honte à moi prochaine fois j'utilise la calculette, ça marche merci de vos conseil !
Ok pour tes calculs qui sont bien en accord avec les généralités de mon premier message.
Pour ton dernier message tu peux vérifier que pour w=wo, on obtient pour les deux filtres :
H=Hmax/
2 avec Hmax=1
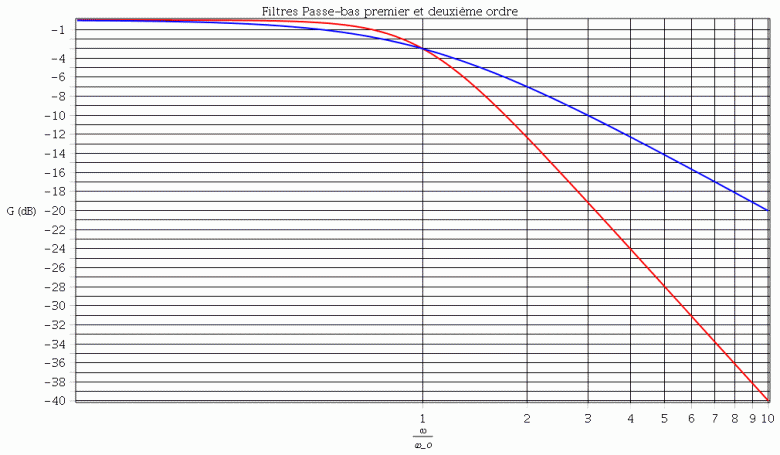
Pour illustrer les propos précédents, voici dans le même repère, les diagrammes de Bode du gain pour les deux filtres passe-bas : en bleu : le filtre du premier ordre ; en rouge : le filtre du deuxième ordre.
On voit bien que le filtre du deuxième ordre a un comportement plus proche du comportement idéal qui correspondrait à G=OdB pour w<wo et à G 
-
pour w>wo
On voit bien que pour w=3wo :
G=-10dB pour le premier ordre ;
G=-19dB pour le deuxième ordre.
Annuler
connectez vous