Inscription / Connexion Nouveau Sujet
filtrage disque vinyles
Bonsoir ! j'aimerais votre aide car je ne vois pas comment faire pour certaine question,
l'égalisation RIAA( Recording association of america) est un standard pour l'enregistrement et la restitution de disque vinyles. Lors de la lecture le signal électrique est envoyé dans un filtre dont la fonction de transfert (normalisée) est :
H(jw)=
1) le diagramme de bode en gain d'un filtre RIAA est représenté sur la figure en dessou, parmi d'autre gains, Déterminer en le justifiant, laquelle des quatres courbes correspond au gain du filtre étudieé
Je pense que celui en pointillet qui est le + noir car avec une tel fonction qu'on peut evaluer en basse frequence, on obtient 1/ 2
2
2) Les trois constantes de temps intervenant dans la fonction de transfert sont 75 s, 318
s, 318 s et 3180
s et 3180 s. On suppose t2>t3. attribuer sans calcul mais en justifiant chaque valeur aux constantes t1, t2 et t3
s. On suppose t2>t3. attribuer sans calcul mais en justifiant chaque valeur aux constantes t1, t2 et t3
je ne vois pas comment faire pour attribuer, y'a-t-il une règle de comment procéder ?
3) Mesurer sur la figure le gain à la fréquence f=50Hz, justifier le résultat obtenu
si c'est bien la figure de la question 1 alors on obtient -4dB, pour justifier il faudrait evaluer l'amplitude de notre fonction je pense
4) a quelle fréquence le gain normalisé est-il égal à -32dB
graphiquement pour 4000Hz ?
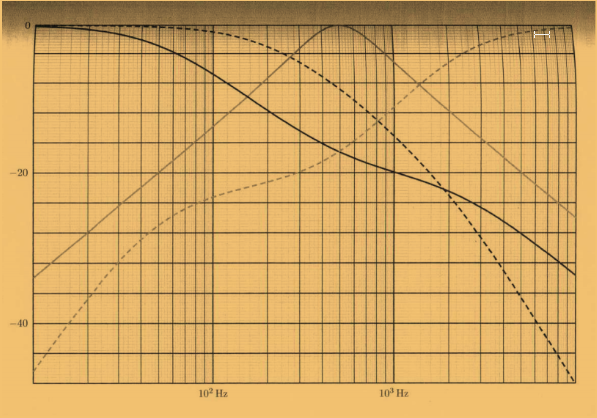
Ah oui c'est plus claire ! mais je ne comprend pas pourquoi la fréquence de pivot dans le lien c'est 1kHz pour obtenir un gain de 0dB, enfin pourquoi on commence pas à la meme echelle ?
1) du coup c'est la courbe tout en noir, et pour le justifier je dois faire des cas ou la pulsation est petit puis grand ?
2) je ne sais toujours pas comment le faire
3) -3dB ?
4) 7kHz ?
Par rapport au document que je t'ai indiqué, toutes les fréquences sont ici atténuées mais le principe est le même : atténuer davantage les hautes fréquences, et cela de façon non linéaire. Pour identifier les trois durées caractéristiques, tu peux remarquer :
Commence par calculer les trois fréquences telles que t. =1 où t est une des trois durée caractéristiques. L'identification sera aisée ensuite.
=1 où t est une des trois durée caractéristiques. L'identification sera aisée ensuite.
J'arrive pas à voir comment vous obtenez après le 10log, normalement comme c'est en facteur le t2*w et t3*w ne devrait pas etre sans puissance ? de meme qu'un facteur 10 sur le dernier log ?
Je pense que tu devrais commencer par revoir ton cours de math sur les nombres complexes et les logarithmes. Le module d'un produit est égal au produit des modules ; le module d'un quotient est égal au quotient des modules. Ta fonction de transfert peut s'écrire sous la forme :
Pour chacun des trois cas, dans la mesure où l'axe horizontal du diagramme de Bode est gradué en fréquence, je te conseille d'écrire le produit t. sous la forme :
sous la forme :
donc :
Ayant ainsi les trois valeurs de fo, il te sera plus simple d'identifier les trois indices... Il ne s'agit pas de jouer aux devinettes !
Effectivement j'ai cette formule mais enfaite je vois pas comment identifier, enfin qu'est-ce qui me permet de dire que ce temps correspond à t2 et pas à t1 enfin de ce genre la
Pour illustrer mon message du 15-01-19 à 11:54 :
J'ai tracé :
En vert : (-G2)
en bleu foncé : (G1)
en cyan : (-G3)
En rouge : le diagramme de Bode du gain fourni par ton énoncé :
G=G1-G2-G3
Cela devrait t'aider...
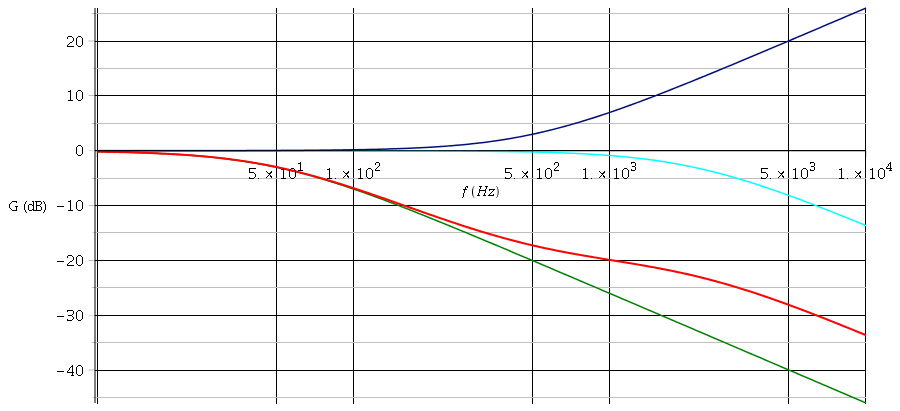
C'est trop bien ! merci de votre courbe génial ! bah du coup en prenant t*w=1 avec chacun des 3 fonctions des gains G1, G2 et G3
Avec G1 on obtient +3dB, ce qui correspond sur sa courbe a 500Hz donc t1=318microseconde
Avec la courbe de G2 on obtient -3dB qui correspond à 3180microseconde donc t2
et du coup t3=75us en fesant de meme ?
Mais bon honnetement meme si c'est ça je ne vois pas comment vous faites pour tracer une telle courbe, comme elle n'etait pas fourni je n'aurai pas pu les retrouver autrement, si ?
Pour vraiment comprendre, il faut commencer par calculer les trois fréquences caractéristiques fo, dans la mesure où l'axe horizontal du diagramme de Bode est gradué en hertz. As-tu fait ce calcul comme expliqué dans mon message du 15-01-19 à 19:32.
Oui, on peut donc identifier a quelle frequence ca correspond quand on regard a 3dB, du coup cest les bon temps ? Ou jai mal lu le graphique ?
?
Quelles sont les trois fréquences caractéristiques fo que tu as calculées ? Ce n'est qu'ensuite qu'il est possible de leurs mettre des indices en tenant compte de l'allure du diagramme de Bode. Je t'ai, sous forme graphique, fourni le résultat mais il faut être capable de le justifier.
En calculant les 3 fréquence j'ai :
2122hz donc courbe cyan, 500hz donc courbe bleu foncé, puis j'ai 50hz courbe verte, et pour justifier on utilise les allures des 3 courbes ?
Telle que j'ai compris la question posée, tout doit se déduire du diagramme de Bode qui est fourni et que j'ai reproduit en rouge.
1° : pour les basse fréquences, le diagramme est assimilable à un passe bas du premier ordre : G=0 aux très basses fréquences puis courbe assimilable à une droite de pente -20dB/décade. La fréquence de coupure à -3dB vaut 50Hz. On à donc :
H 1/H2 avec H1
1/H2 avec H1 1 ; H3
1 ; H3 1.
1.
G -G2 avec G1
-G2 avec G1 0 ; G3
0 ; G3 0
0
Cela conduit donc à f02=50Hz ; t2=3180µs. On peut donc tracer la courbe verte.
On remarque que le diagramme de Bode est superposable à la courbe verte jusqu'à f=150Hz environ. Ensuite, Le diagramme de Bode est au-dessus de la courbe verte. Il faut donc, pour obtenir G, ajouter à -G2 une quantité positive. Il ne peut s'agir que de G1. Donc f01=500Hz ; t1=318µs.
On en déduit par élimination f03=2133Hz et t3=75µs. On peut remarquer, mais cela n'est pas demandé ici que, pour f>f03 on retombe sur une droite de pente -20dB/dec.
Pour résumer, tu peux retenir pour ce type de filtre, que la constante intermédiaire figure au numérateur, les constantes extrêmes étant au dénominateur.


