Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Expression de cordonnées dans différentes bases

Posté par
Kai22 13-02-17 à 14:25

Bonjour.

Je bloque sur un exercice de cinématique dont voici le sujet :
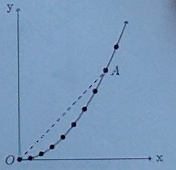
Un point M est mobile dans un plan (O;ux;uy) sur une trajectoire parabolique d'équation y = 1/(4a)*x2. La longueur a permet d'exprimer x et y dans la même unité, le mètre. On prendra a=1,0 m. Le mobile est en O à l'instant initial t=0s et un enregistrement de la position de M est effectué toutes les secondes avec =0,04s.

1) Quelle est la vitesse instantanée du mobile en chacun des points M(t=n)?
Donner les coordonnées du vecteur vitesse dans la base cartésienne K(ux;uy).

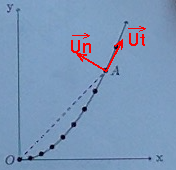
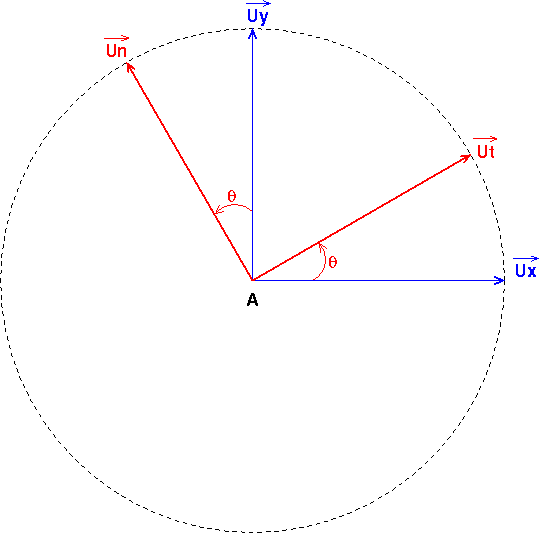
2) Déterminer dans K les composantes des vecteurs unitaires ut et un respectivement tangent (dans le sens du mouvement) et normal (dirigé vers l'intérieur de la parabole) au point A de la trajectoire.
Donner l'expression du vecteur vA dans la base I(ut;un).
Calculer la valeur de l'angle =(ux;ut) en A.

Je joins immédiatement le schéma de la parabole ainsi que le tableau de valeurs.

1) J'ai trouvé v=10(ux) + 2n(uy). La correction m'indique que c'est la bonne réponse.

2) C'est ici que je ne comprends absolument pas la méthode.
Le corrigé indique que \vec{ut}=\vec{v}/\parallel v\parallel avec \vec{v}=\frac{dx}{dt}\vec{ux}+\frac{dy}{dt}\vec{uy} \vec{v}dt=dx\vec{ux}+dy\vec{uy} \frac{\vec{v}dt}{dx}=\vec{ux}+\frac{dy}{dx}\vec{uy} ce que je ne comprends pas (je suis assez "choquée" par les manipulations de dérivées...).
Ensuite ça part sur du \vec{ut}//\vec{ux}+\frac{dy}{dx}\vec{uy} et je ne comprends rien à cette méthode.

Pouvez-vous m'aidez ?

Un grand merci par avance.

Posté par
Kai22re : Expression de cordonnées dans différentes bases 13-02-17 à 14:30

Voici les documents.

Expression de cordonnées dans différentes bases

Posté par
Kai22re : Expression de cordonnées dans différentes bases 13-02-17 à 14:30

Et voilà.

Expression de cordonnées dans différentes bases

Posté par
vanoisere : Expression de cordonnées dans différentes bases 13-02-17 à 15:11

Bonjour
En ce qui concerne le vecteur Ut, je pense que ton corrigé complique la situation. Il suffit d'écrire que ce vecteur est unitaire et colinéaire au vecteur vitesse. Cela donne, comme déjà écrit :

\overrightarrow{v}=10\overrightarrow{u_{x}}+2n\overrightarrow{u_{y}}\quad;\quad\Vert\overrightarrow{v}\Vert=\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{100+4n^{2}} \\
D'où l'expression du vecteur Ut :

\overrightarrow{u_{t}}=\frac{\overrightarrow{v}}{\Vert\overrightarrow{v}\Vert}=\frac{10}{\sqrt{100+4n^{2}}}\cdot\overrightarrow{u_{x}}+\frac{2n}{\sqrt{100+4n^{2}}}\cdot\overrightarrow{u_{y}}

Posté par
vanoisere : Expression de cordonnées dans différentes bases 13-02-17 à 15:13

Je te laisse réfléchir à la suite... Pose de nouvelles questions sur ce que tu ne comprends pas...

Posté par
Kai22re : Expression de cordonnées dans différentes bases 13-02-17 à 15:28

En effet, c'est beaucoup plus simple comme cela.
Au fait, pourquoi a-t-on \vec{ut}=\frac{\vec{v}}{v} ?

Posté par
vanoisere : Expression de cordonnées dans différentes bases 13-02-17 à 15:39

C'est indiqué dans l'énoncé : le vecteur Ut est un vecteur unitaire (norme égale à 1) ayant la direction et le sens du vecteur vitesse. Il est donc possible d'écrire :

\overrightarrow{v}=\Vert\overrightarrow{v}\Vert\cdot\overrightarrow{u_{t}}

Posté par
vanoisere : Expression de cordonnées dans différentes bases 13-02-17 à 15:49

Ce schéma t'aidera peut-être pour la suite...

Expression de cordonnées dans différentes bases

Posté par
Kai22re : Expression de cordonnées dans différentes bases 13-02-17 à 18:10

D'accord, je comprends mieux en effet.
Pour un, je peux passer le produit scalaire ut.un=0 ?

Posté par
vanoisere : Expression de cordonnées dans différentes bases 13-02-17 à 18:45

le produit scalaire des deux vecteurs unitaires doit effectivement être nul. Tu peux aussi remarquer que l'on passe de Ut à Un par une rotation de 90° dans le sens trigonométrique...

Expression de cordonnées dans différentes bases

Posté par
diracre : Expression de cordonnées dans différentes bases 13-02-17 à 19:17

Hello à tous les 2

Une parenthèse que j'ouvre  ... Vanoise ayant déjà tout dit.  Juste parce que j'ai toujours trouvé "belles" les lignes suivantes

\vec{u}_T.\vec{u}_T = 1

Donc

\frac{d}{dt}(\vec{u}_T.\vec{u}_T) = 0

Donc

2.\vec{u}_T.\frac{d}{dt}(\vec{u}_T) = 0

Donc

\vec{u}_T  et  \frac{d}{dt}(\vec{u}_T)  sont orthogonaux

Ou bien

\vec{u}_N  et  \frac{d}{dt}(\vec{u}_T)  sont colinéaires

Je referme ma parenthèse et je vous laisse bosser  

Posté par
vanoisere : Expression de cordonnées dans différentes bases 13-02-17 à 19:55

Bonjour dirac
Tes remarques sont intéressantes pour étudier les 2 composantes de l'accélération mais nous n'en sommes pas encore là!


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !