Inscription / Connexion Nouveau Sujet
Exo méca pendule en rotation
Bonjour, j'aurais besoin de votre aide pour l'exercice suivant.
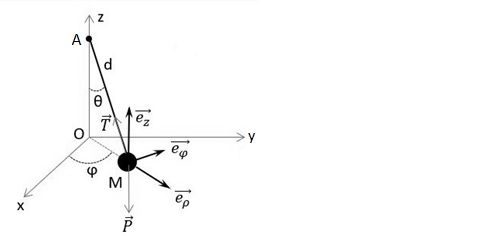
On se place dans un référentiel galiléen R, et on y associe le repère orthonormé (O, ex, ey, ez). On considère le mouvement d'un objet noté M, de masse m, qui est suspendu à un point A sur l'axe z, par un fil inextensible de longueur l. Cet objet a un mouvement rotatoire dans le plan (xOy), et ce autour de l'axe Oz.
J'ai besoin de votre aide pour les questions suivantes car je ne sais pas comment faire.
1) Grâce à la L.F.D., écrivez les 3 équations scalaires du mouvement de l'objet M.
-> je sais qu'il faut faire somme des forces extérieures = m*accélération = vect P + vect T = ... mais je ne sais pas dans quelle base travailler (cartésienne, cylindrique, sphérique, ...).
2) Montrez maintenant que M a un MCU.
-> selon moi il faut montrer que pas d'accélération et/ou pas de vitesse radiale (donc pas en fonction de e(phi))
3) Calculez les moments cinétiques de M en A et de M en O par rapport au référentiel R.
-> je connais la formule mais je ne sais pas comment l'appliquer sans avoir répondu aux questions précédentes
4) Calculez le moment des forces en O.
5) Déterminez l'expression de T en fonction de teta et des données de l'exercice.
-> je pense utiliser le TCM en O mais je ne sais pas comment faire
Merci par avance pour votre aide !
Bonjour
Si tu commençais pas expliquer ce que tu as fait et ce qui te bloque ? Plus facile de t'aider ensuite en tenant compte de ton niveau et de ton programme !
Bonjour,
Le dessin suggère la base à utiliser pour projeter le PFD
En plus pour étudier un mvt circulaire, les coordonnées cartésiennes ne sont pas vraiment appropriées!
PS : pour affirmer que le mouvement est circulaire et uniforme, une donnée est manquante. Vérifie si rien n'est précisé sur  ou sur la dérivée de
ou sur la dérivée de  par rapport à t.
par rapport à t.
Bonsoir à tous !
Pour l'instant je n'ai pas fait grand chose, j'ai seulement énoncé les grandes lignes de ce que je compte faire car je ne sais pas par où commencer.
J'ai utilisé la base cylindrique pour le PFD. Je trouve donc vecteur P = -mg e(z), vecteur T = - T * sin (teta) e(rho) + T cos (teta) e(z) et m*a = -m*l*sin(teta)*phi² e(rho), ce qui me donne, en développant, deux équations scalaires : T = m*l*phi² et mg = T*cos(teta). Je pense avoir une erreur car je trouve seulement 2 équations scalaires au lieu de 3.
En ce qui concerne le mouvement circulaire uniforme, on sait seulement que le fil fait un angle teta avec l'axe Oz. On nous conseille également d'utiliser une des équations scalaires pour montrer que M fait un MCU.
Pour ce qui est de l'accélération dans la base cylindrique, je dirais que c'est ma = - m * l * teta . ² e(rho) + m * l * teta .. e(phi) mais je ne suis vraiment pas sûre...
Bon finalement après m'être encore trompée, je pense maintenant que m*a dans la base cylindrique vaut : l*sin(teta)*teta . ² e(rho) - l*sin(teta)*teta.. (".." = dérivée seconde). Aidez-moi svp parce que là je n'y arrive pas du tout 
Attention, la rotation se fait autour de (Oz)
Ici  est constant
est constant
Utilise les symboles en appuyant sur l'icône  en bas de la fenêtre d'édition et utilise plutôt " et ' pour les dérivées
en bas de la fenêtre d'édition et utilise plutôt " et ' pour les dérivées
Le mouvement de M se produisant dans le plan (Oxy), l'angle  reste fixe... Première chose à préciser.
reste fixe... Première chose à préciser.
Tes projections des vecteurs T et P sont correctes. Pour l'accélération, il faut tenir compte de la composante tangentielle et de la composante normale. Cela donne :
avec :
La longueur du pendule est notée « l » dans l'énoncé et « d » sur le schéma...



