Niveau maths sup

Exo Filtre coup-bande.

Posté par
camus11 16-01-11 à 17:33

Bonjour,
Petit exo sur les filtres, je sais ce qu'il faut faire mais je n'arrive pas à un résultat satisfaisant.

Enoncé :
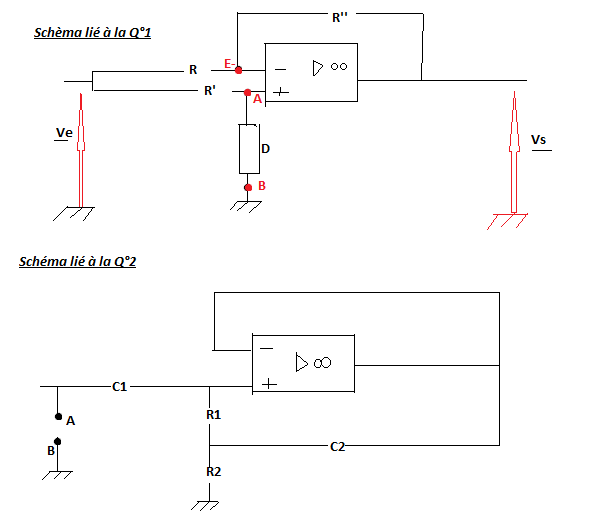
1). Déterminer l'impédance Z du dipôle D pour que la fonction de transfert H=Vs/Ve soit nulle.
2). Le dipôle [AB] est associé au montage ci-dessous :
a/. Déterminer son impédance d'entrée Ze.
b/. Peut-on réaliser la condition imposée à la première question ? Tracer /H/ et en fonction de log().

Réponses :

1). J'utilise Millman en E- et je trouve Ve-=(R''*Ve+RVs)/(R+R'')
Ensuite j'utilise Millman en A, et je trouve Ve+=(Ve*Z)/(R'+Z).
Et commme l'AO est idéal, alors on a V+=V-.
Donc on a les deux expressions précédentes égales, puis j'ai voulu avoir l'expression de Vs/Ve cependant je me trouve à chaque fois avec du Ve de l'autre côté de l'égalité au lieu de n'avoir que du Z,R,R' et R''.
Puis quand j'aurais la fonction de transfert, il sera aisé de trouvé pour quelle valeur de Z elle s'annule.

2).
a/.Ici, je ne vois pas trop. Je pourrais utiliser Millman au niveau de l'intersection entre C1 et R1 mais je ne vois pas trop à quoi ca pourrait me servir. Surtout que je ne peux pas calculer V- (enfin je ne vois pas comment tout du moins).
b/. Pour celle-ci, après avoir obtenu Ze, il faut voir si son expression est pareil que celle trouvée à la question 1). je suppose?
Puis, pour le tracé de /H/ et de pas de problème. Il suffit de calculer la fonction de transfert, puis en ayant la forme normalisée. On calcule son module et on fait une étude qualitative et asymptotique pour avoir le tracé de la fonction réelle.

Merci.

Exo Filtre coup-bande.

Posté par re : Exo Filtre coup-bande. 16-01-11 à 17:46

Salut,

que proposes-tu ?

Posté par re : Exo Filtre coup-bande. 16-01-11 à 17:47

1. C'est la bonne méthode oui

Posté par re : Exo Filtre coup-bande. 16-01-11 à 18:12

Ce que je propose? Eh bien, je ne sais pas trop justement.^^'
Pour la 1)., je tombe sur une expression incorrecte soit :

Vs/Ve = Ve*(Z(R+R'')-R'+Z)/(R'R'' +ZR'') * (Z(R+R'')-R'+Z)/(RR'+ZR)
Evidemment, ce n'est pas bon, et c'est le Ve qui me gène =/

En ce qui concerne la question 2, je n'ai pas grand chose à proposer que ce que j'ai mentionné précédemment. Au niveau du dipôle on a une tension Ve' qu'il faudrait calculer pour trouver l'expression de Ze mais comme on ne peut faire Millman qu'au niveau de la borne + de l'AO et pas de la borne -, eh bien je n'y arrive pas.

Posté par filtre 16-01-11 à 19:05

Bonsoir,

Pour la question 1 vos relations sont correctes.

Je trouve sauf erreur vs/ve = (Z-R'R''/R)/(Z +R')

A vous lire. JED.

Posté par re : Exo Filtre coup-bande. 17-01-11 à 20:02

Bonsoir,

Ah oui, après avoir refait mes calculs je tombe bien sur la même formule :

Ve-=Ve+
(RVs+R"Ve)/(R+R")=(ZVe)/(Z+R')
Puis produits en croix, et simplification :
Vs=Ve* (RZ-R'R")/(RZ+RR')
Vs/Ve= (RZ-R'R")/(R(Z+R'))

D'où, la fonction de transfert s'annule pour Z=(R'R")/R .

2/. Pour calculer Ze j'ai du mal :
On a une tension d'entrée Ve' au borne de AB.
J'utilise millman (au point d'intersection entre R1 et C1), cela donne :

V+(1/jC1 + 1/R1)= Ve'[u]/jC1 + [u]Vs'/R1
D'où après simplifaction on obtient finalement :
V+= (Ve'R1+Vs'jC1)/(R1+jC1)
Mais après je ne peux pas refaire Millman, et surtout je ne vois pas comment y introduire l'impédance Ze du dipôle AB.

Posté par re : Exo Filtre coup-bande. 18-01-11 à 20:43

Bonsoir,
En général, pour calculer Z_e d'un montage, on applique une tension V_e à l'entrée et on calcule I_e (courant d'entrée) et Z_e = V_e / I_e.
Pour cela, il faut évidemment exprimer V_s en fonction de V_e pour éliminer V_s.
Là, j'ai fait d'une autre façon. L'impédance d'entrée est composée de C₁ en série avec l'impédance se trouvant entre l'entrée + et la masse (l'entrée de l'ampli op n'intervient pas puisqu'il est supposé parfait).
Le courant I_e traverse C₁ et passe par R₁ ensuite.
Si j'appelle P le point de jonction entre R₁, R₂ et C₂ (Millman) :
$3$V_P\,=\,\frac{\frac{v^+}{R_1}\,+\,jC_2\omega\,V_1}{\frac{1}{R_1}\,+\,\frac{1}{R_2}\,+\,jC_2\omega}$
En tenant compte du fait que v⁺ = v^- = V_s :
$3$V_P\,=\,\frac{R_2V_s\,+\,jR_1R_2C_2\omega\,V_s}{R_1\,+\,R_2\,+\,jR_1R_2C_2\omega}$
Le courant dans R₁ est le courant d'entrée I_e :
$3$I_e\,=\,\frac{v^+\,-\,V_P}{R_1}$
En remplaçant V_P, on finit par obtenir :
$3$v^+\,=\,(R_1\,+\,R_2\,+\,jR_1R_2C_2\omega)\,I_e$
On a:
$3$V_e\,=\,(V_e\,-\,v^+)\,+\,v^+$

$3$V_e\,=\,\frac{1}{jC_1\omega}\,I_e\,+\,(R_1\,+\,R_2\,+\,jR_1R_2C_2\omega)\,I_e$
D'où :
$3$Z_e\,=\,\frac{1}{jC_1\omega}\,+\,R_1\,+\,R_2\,+\,jR_1R_2C_2\omega$

Voilà pour le calcul de Z_e... Ce n'est pas tout à fait fini mais je complèterai si besoin est.
J'espère ne pas avoir fait de fautes de recopie.