Inscription / Connexion Nouveau Sujet
Exercice unités et dimensions
Bonjour, j'ai des doutes sur cet exercice, pouvez-vous m'aider ?
->
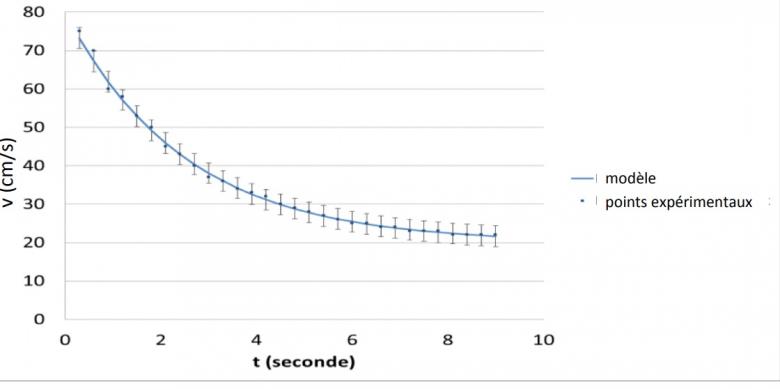
Un étudiant mesure l'évolution temporelle de la vitesse v(t) d'un objet sphérique tombant dans un fluide, et donc soumis à une force de frottement. L'étudiant obtient une courbe v(t) reproduite ci-dessous.
Cette courbe est en accord avec le modèle qu'il a développé : v(t) = vlim + K e(-t/ )
)
où vlim est la vitesse limite atteinte par la sphère.
1. Quelles sont les dimensions des constantes K et τ , et leurs unités dans le système SI?
2. Montrer qu'en traçant ln(v(t) − vlim) en fonction de t, l'étudiant doit obtenir une droite.
3. Donner l'ordonnée à l'origine et la pente de cette droite en fonction de K et τ [ça je pense que ça devrait aller, mais au cas où]
Merci d'avance !
Bonjour,
Deux indices:
- v(t) doit être homogène à une vitesse..
- L'exponentielle ne peut être que sans dimension (une exponentielle de temps ou de distance n'a pas de sens).
Qu'est-ce qu'une fonction homogène ?
Concernant les exercices :
1. v(t) et vlim sont en m.s-1, donc je suppose que Ke(-t/ ) n'a pas de dimension. Donc si une exponentielle n'a pas de dimension alors K ne doit pas en avoir non-plus.
) n'a pas de dimension. Donc si une exponentielle n'a pas de dimension alors K ne doit pas en avoir non-plus.
Par contre pour  je sais pas comment le déterminer. Quand tu dis qu'une exponentielle est sans dimension, est-ce que ça veut dire que
je sais pas comment le déterminer. Quand tu dis qu'une exponentielle est sans dimension, est-ce que ça veut dire que  est en s-1, ce qui fait que t/
est en s-1, ce qui fait que t/ est sans dimension et que PAR CONSEQUENT e(-t/
est sans dimension et que PAR CONSEQUENT e(-t/ ) aussi, ou est-ce qu'une exponentielle est sans dimension quoi qu'il arrive (auquel cas je ne sais pas quoi faire) ?
) aussi, ou est-ce qu'une exponentielle est sans dimension quoi qu'il arrive (auquel cas je ne sais pas quoi faire) ?
2. Je suppose que :
v(t) = vlim + Ke(-t/ )
)
v(t) - vlim = Ke(-t/ )
)
ln(v(t) - vlim) = ln(Ke(-t/ ))
))
ln(v(t) - vlim) = ln(K) + ln(e(-t/ ))
))
ln(v(t) - vlim) = ln(K) - t/
Et comme K et  sont des constantes, alors ln(K) - t/
sont des constantes, alors ln(K) - t/ est une droite.
est une droite.
C'est bien ça ?
3. Ordonnée à l'origine c'est quand on prend "t=0", donc ln(K)
et la pente c'est "y2-y1 / x2-x1", donc si on prend "x1 = 0" et "x2 = t" ça donne :
(ln(K) - t/ - ln(K)) / (t - 0)
- ln(K)) / (t - 0)
(- t/ ) / t
) / t
(- 1/ )
)
Voilà, dites-moi si c'est bon !
1)
v(t) = vlim + K e(-t/tau)
[v(t)] = L.T^-1 et l'unité SI de v(t) est le m/s
[vlim] = L.T^-1 et l'unité SI de vlim est le m/s
[K] = L.T^-1 et l'unité SI de K est le m/s
[t/tau] = 1 (sans dimension) et donc [t] = [tau]
[t] = T et l'unité SI de t est la s
[tau] = T et l'unité SI de tau est la s
-----
2)
Il y a un os dans l'énoncé ... si K < 0 (et c'est bien le cas si on se fie au graphe donné)
L'objet est "lancé" à vitesse initiale > Vlim, non nulle vers le bas dans le fluide.
Si c'est le cas, alors on a v(t) > Vlim pendant toute la mesure et donc (v(t) - vlim) < 0 ... ce qui fait que ln(v(t) − vlim) n'existe pas.
v(t) = vlim + K e(-t/tau)
(v(t) - vlim) = K.e(-t/tau)
a) Si K < 0, (v(t) - vlim) < 0
et on a : |(v(t) - vlim)| = |K|.e(-t/tau)
b) Si K > 0, (v(t) - vlim) > 0
et on a : |(v(t) - vlim)| = |K|.e(-t/tau)
On peut donc traiter |(v(t) - vlim)| = |K|.e(-t/tau) quel que soit le signe de K
On prend le ln des 2 membres :
ln|(v(t) - vlim)| = ln[|K|.e(-t/tau)]
ln|(v(t) - vlim)| = ln[|K|] + ln[e(-t/tau)]
ln|(v(t) - vlim)| = ln[|K|] - t/tau
ln|(v(t) - vlim)| est de la forme At + B (qui est l'équation d'une droite de variable t)
avec A = -1/tau et B = ln|K|
Reste à voir si le problème que j'ai mentionné au début de la question a effleuré le prof ou si cela lui est passé au dessus de la tête.
-----
Sauf distraction. 


