Inscription / Connexion Nouveau Sujet
exercice tube cylindrique
Bonsoir,
J'ai un soucis au niveau de la compréhension d'une question qui ne me permet pas de trouver la démarche nécessaire pour répondre a l'exercice.
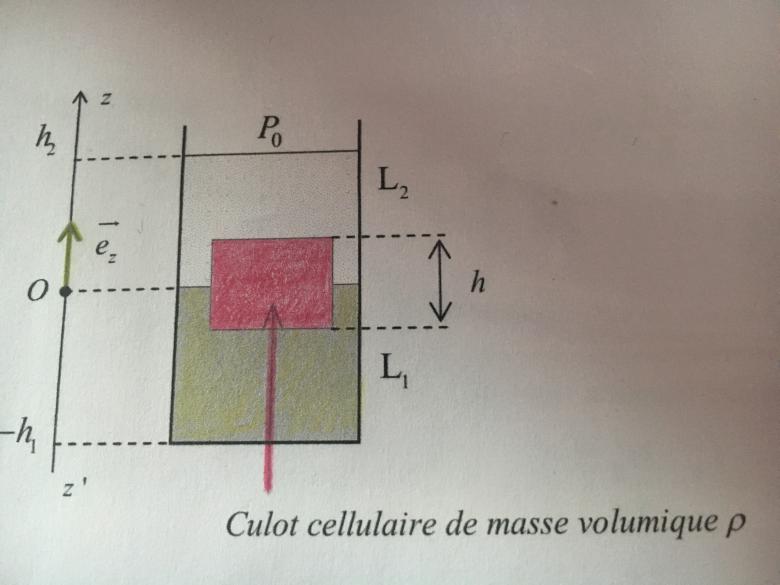
Ci joint le schéma de l'exercice je précise que le cylindre est pris en 3 parties c'est a dire on a le bas du cylindre avec un liquide L1 de masse volumique rho 1 de hauteur h1
Ensuite on a le culot qui flotte de longueur H et de masse volumique rho
et enfin le second liquide L2 au dessus non miscible avec L1 et de mase volumique rho2¨
La question demandé est quel masse volumique rho 2 permet une répartition du culot cellulaire a part égale entre L1 et L2 en connaissant rho et rho1
Sachant que dans la question précédente l'exercice demande de calculer la pression p(z) dans le liquide L1
Voila vraiment j'ai besoin de quelque pistes parce que je trouve pas quel équation permettrait de trouver rho 2 pour que le culot reste en equilibre
Un grand merci cette question me tracassait haha 
Bonsoir Krinn!
Tout d'abord merci de m'avoir repondue
Euh alors je dirais que l'equilibre s'obtient lorsque la somme des forces est nulle ? 
Bonjour ,
Le demandeur ne semble pas revenir ...
Ma réponse : Rho2 = 2 Rho - Rho1
Cela me paraît trop facile et mon raisonnement me semble faux ,
seulement , je ne sais pas quoi faire d'autre ...
Salut,
C'est correct.
Si on fait appel à la poussée d'Archimède ... il faut justifier que c'est applicable.
Et sans faire appel directement à Archimède, on peut le faire ainsi :
Pression sur la face haute du culot : Ph = Po + Rho2 * g * (h2 - h/2)
Pression sur la face basse du culot : Pb = Po + Rho2 * g * h2 + Rho1 * g * h/2
Poids du culot : P = Rho * g * S * h
Le culot est en équilibre et donc :
P + Ph * S - Pb * S = 0
Rho * g * S*h + Ph * S - Pb * S = 0
Rho * g * h + Ph - Pb = 0
Rho * g * h + (Po + Rho2 * g * (h2 - h/2)) - (Po + Rho2 * g * h2 + Rho1 * g * h/2) = 0
Rho * h + (Rho2 * ( - h/2)) - (Rho1 * h/2) = 0
Rho2 * h/2 = Rho * h - Rho1 * h/2
Rho2 = 2.Rho - Rho1
Sauf distraction. 
Merci ,
C'est bien plus court avec Archimède , mais justement comment justifier que c'est applicable ?
J'écris la poussée sur le 1/2 bloc haut , MAIS sa face inférieure n'est pas immergée ...
Donc , je n'ai pas le droit ?
Bonsoir
Perso, j aurais aussi utilise Archimede si majo4 avais insisté
Car je ne vois pas ce qui nous en empêche ici
Mais je n'ai pas la rigueur de JP
Qui a évité l écueil de façon magistrale
C'est bien plus court avec Archimède , mais justement comment justifier que c'est applicable ?
Par exemple en résolvant comme je l'ai fait et en se rappelant que la poussée d'Archimède n'est rien d'autre que la résultante des forces de pressions sur l'objet.

J-P
Je pense avoir compris !
Que trouves-tu ?

Coucou J-P
Alors en prenant appuie sur la formule de la pousée d'archimède cela a donné :
la résultante = ( rho S - Rho F ) * V * g
Pour avoir l'equilibre la resultante des force doit être nulle
donc Rho S - Rho F = 0
et la pour le coup je vous avoue qu'en relisant mes notes mon equation paraissait logique mais en fait je ne comprends plus haha j'ai mis
rho 2 = Rho 1 - Rho/2 ....
Je pense reprendre ta demonstration pour être sure de tomber sur vos resultats mais j'ai un soucis je pense au niveau de la compréhension
Merci a tous de vos réponses qui m'ont énormément aidé

Après avoir repris votre cheminement je comprends finalement comment on retombe sur rho 2 = 2 rho 1 - Rho
Un grand merci
Mais je n'arrive pas a retomber dessus en repartant juste de la formule de la poussée d'archimède je tombe encore sur rho 2 = rho 1 - rho/2... 
En allant très vite :
M: masse du culot
S : Aire de la base du culot
M1: masse du liquide 1 déplacé par le culot
M2: masse du liquide 2 déplacé par le culot
Le poids P = Mg du culot est équilibré par les deux poussées P1 = M1*g et P2=M2*g des liquides 1 et 2
Mg = M1*g + M2*g (Condition d'équilibre)
donc M = M1 + M2
Avec M =  *S*H
*S*H
M1 =  1*S*(H/2)
1*S*(H/2)
M2 =  2*S*(H/2)
2*S*(H/2)
Soit :  H =
H =  1*H/2 +
1*H/2 +  2*H/2
2*H/2
Et après simplifications :  2 = 2
2 = 2 -
-  1
1
En allant très vite :
M: masse du culot
S : Aire de la base du culot
M1: masse du liquide 1 déplacé par le culot
M2: masse du liquide 2 déplacé par le culot
Le poids P = Mg du culot est équilibré par les deux poussées P1 = M1*g et P2=M2*g des liquides 1 et 2
Mg = M1*g + M2*g (Condition d'équilibre)
donc M = M1 + M2
Avec M =
 *S*H
*S*H
M1 =
 1*S*(H/2)
1*S*(H/2)
M2 =
 2*S*(H/2)
2*S*(H/2)
Soit :
 H =
H =  1*H/2 +
1*H/2 +  2*H/2
2*H/2
Et après simplifications :
 2 = 2
2 = 2 -
-  1
1Un enorme merci

Juste quelques mots pour expliquer les réticences de quarkplus (qui confirmera ou infirmera) quand il a écrit :
" Cela me paraît trop facile et mon raisonnement me semble faux ,
seulement , je ne sais pas quoi faire d'autre ..."
Réticence qu'il a bien expliqué par
Merci ,
C'est bien plus court avec Archimède , mais justement comment justifier que c'est applicable ?
J'écris la poussée sur le 1/2 bloc haut , MAIS sa face inférieure n'est pas immergée ...
Donc , je n'ai pas le droit ?
Cela a le grand mérite de montrer que ce n'est pas évident de pouvoir appliquer dans ce cas, le calcul habituel de la poussée d'Archimède ... sachant qu'elle est la résultante des forces de pressions sur l'objet.
----------------
On peut utiliser la poussée d'Archimède ... mais ce n'est pas si évident que cela
Si on utilise le formulation souvent utilisée (mais incomplète) de la poussée d'Archimède, soit ;
« Tout corps plongé dans un fluide au repos, subit une force verticale, dirigée de bas en haut et opposée au poids du volume de fluide déplacé ; cette force est appelée poussée d'Archimède. »
On peut penser que c'est évident et que Archimède peut être utilisé.
Mais si on utilise la formulation plus complète (et plus correcte) soit :
« Tout corps plongé dans un fluide au repos, entièrement mouillé par celui-ci ou traversant sa surface libre, subit une force verticale, dirigée de bas en haut et opposée au poids du volume de fluide déplacé ; cette force est appelée poussée d'Archimède. »
On peut alors se poser des questions...
-----
Il y a une différence fondamentale entre ces 2 formulations, différence qui ne permet pas (par exemple) d'utiliser le calcul "habituel" lorsque l'objet touche "quelque chose", par exemple le fond ou même un bord du récipient. (et cela est systématiquement "oublié" dans la plupart des exercices sur ce sujet dans le secondaire)
Ici, bien sûr l'objet ne touche ni le fond, ni un bord ... Néanmoins, le liquide du haut n'a pas accés à l'objet au niveau de séparation des 2 liquides et il est donc "normal" d'au moins se poser la question suivante :
Comment le liquide du haut exerce-t-il la poussée d'Archimède (VERS le haut) sur le volume de l'objet dans ce liquide ... alors qu'il n'a pas directement accès à la surface de l'objet horizontale au niveau de la séparation des 2 liquides.
Ceci étant dit, on peut démontrer que dans le cas de l'exercice, on peut quand même utiliser le calcul simple par la somme des 2 poussées d'Archimède malgré les remarques ci-dessus ... Mais ce n'est pas si évident que cela à démontrer ... en tenant évidemment compte de la formulation complète et pas faussement raccourcie de la poussée d'Archimède... et cela ne va pas sans dire.

Bonjour
Il existe une démonstration simple, rigoureuse et sans calcul, de l'expression de la poussée d'Archimède sur un solide de forme quelconque. Comme déjà dit, cette force est la résultante des forces de pression exercées sur la surface fermée délimitant le solide par tous les fluides qui l'entourent. On peut toujours considérer le solide entièrement entouré de fluide en prenant l'air atmosphérique en compte, même si son action est parfois négligeable.
On imagine donc un fluide ou un ensemble de fluides en équilibre dans le champ de pesanteur terrestre. On y immerge un solide délimité par une surface fermée (S). On imagine alors que l'on "vide" le solide de sa matière,sans déplacer ni modifier (S), remplaçant cette matière par le ou les fluide(s) qui l'entoure(nt) de façon qu'à une même altitude z, le fluide soit le même à l'intérieur et à l'extérieur de (S). Dans ces conditions, le fluide intérieur est évidemment en équilibre, et cela sous l'action de deux forces :
* la force pressante exercée sur (S) par le fluide extérieur, c'est à dire la poussée d'Archimède ;
*le poids du fluide intérieur.
Conclusion : la poussée d'Archimède est bien l'opposé du poids du (ou des) fluide(s) "déplacés" par le solide... Cette démonstration a aussi l'avantage de clairement préciser ce qu'on entend par "fluide(s) déplacé(s)".
Il existe une démonstration plus "technique" mais pas plus rigoureuse utilisant le théorème du gradient pour une surface fermée et l'expression locale de la statique des fluides :
D'accord ... mais cela n'a rien d'une démonstration.
C'est une suite d'affirmations (correctes) mais non démontrées par cette intervention.
Mais je ne poursuivrai pas sur ce sujet. 

mais cela n'a rien d'une démonstration.
JP pourrait-il développer ?
La surface (S) n'étant ni déplacée ni difformée, la force pressante exercée par le fluide extérieur sur (S) est bien, par définition, la poussée d'Archimède, sous réserve bien sûr que (S) soit immobile, sinon le problème relèverait de la dynamique des fluides.
Si l'intérieur de (S) est remplacée par le fluide dans les conditions que j'ai décrites, le fluide intérieur est bien en équilibre donc...
J'avais oublié de préciser que la poussée d'Archimède représente la résultante des actions du fluides extérieur sur (S) lorsque (S) est immobile dans le fluide. Sinon...
Pour les adeptes de jolies (?) formules, voici le calcul direct des forces de pression exercées par un (ou plusieurs) fluides sur un solide, l'ensemble étant en équilibre dans le champ de gravitation terrestre. Pour alléger le propos, je parlerai de fluide (même s'ils sont en réalité plusieurs ou même si certains fluides ne sont pas homogènes ; cela ne change rien à la démonstration. Je garde la surface (S) fermée délimitant le solide et comme précédemment, sans en modifier ni la forme ni la position, je remplace l'intérieur par le fluide tel qu'expliqué précédemment.
Le fluide fictif intérieur étant en équilibre, la pression en tout point de ce fluide fictif intérieur vérifie la relation :
où  f désigne la masse volumique du fluide réel extérieur à la même altitude. Je commence par exprimer la résultante des forces de pression exercée par ce fluide intérieur fictif sur le fluide extérieur :
f désigne la masse volumique du fluide réel extérieur à la même altitude. Je commence par exprimer la résultante des forces de pression exercée par ce fluide intérieur fictif sur le fluide extérieur :
où P désigne la pression en un point quelconque de la surface,entouré d'un élément de surface , normal à la surface et orienté vers l'extérieur.
Il faut faire intervenir maintenant le théorème du gradient pour transformer l'intégrale de surface en intégrale de volume :
où désigne le gradient de la pression en un point quelconque à l'intérieur de (S) et d
 un volume élémentaire entourant ce point. On peut trouver la démonstration ici :
un volume élémentaire entourant ce point. On peut trouver la démonstration ici :
![]() : fichier : operateurs.pdf , §7 et 8.
: fichier : operateurs.pdf , §7 et 8.
La relation fondamentale de la statique des fluides donne :
La force exercée par le fluide fictif sur le fluide réel à l'extérieur de (S) est tout simplement le poids du fluide fictif intérieur donc le poids du fluide déplacé par le solide. On conclut en appliquant le principe des actions réciproques : la poussée d'Archimède est l'opposé de cette force :
Encore une fois : dans la mesure où le remplacement du solide par un fluide fictif tel qu'expliqué précédemment ne modifie ni la forme, ni la position de la surface (S) ni les caractéristiques du fluide extérieur, l'action de ce fluide extérieur réel sur la surface (S) (la poussée d'Archimède) est donc inchangée par cette opération de "remplacement fictif".



