Inscription / Connexion Nouveau Sujet
Exercice : Trois sources alignées
Bonjour, j'espère que vous allez tous bien.
J'ai de nouveau besoin de votre aide pour un exercice de physique.
-----
On considère trois sources S1, S2 et S3 équidistantes (S1S2 = S2S3 = a = 0, 45mm) et alignées sur une droite parallèle à l'axe Ox du plan d'observation. Les trois sources sont cohérentes et émettent une onde lumineuse de même amplitude AO. On notera I0 l'intensité. Le plan d'observation est à grande distance , D = 3m, des sources.
-----
1. Établir l'expression I(x) de l'intensité en un point M du plan d'observation.
2. Établir l'expression I'(x) de l'intensité en un point M du plan d'observation si on obstrue la source S2.
3. Tracer sur un même graphe les intensités I(x) et I'(x) pour −λDa < x < λDa en précisant les positions des maxima et des minima.
Pour la question 1 il faut trouver y1, y2 et y3 puis les sommer puis extraire l'amplitude A pour trouver I(x) tel que : I(x) = Io * A2 ? Dans ce cas y a t il un déphasage entre y1, y2 et y3 ?
Merci d'avance de votre aide.
Bonjour
Commence par calculer le déphasage en M entre les ondes 2 et 1. Facile ensuite d'obtenir celui entre les ondes 3 et 2. Puis somme des 3 signaux.
Une remarque concernant l'énoncé ; celui-ci fournit-il une indication sur la valeur de ? Si le cosinus de cette expression n'a pas une valeur simple (0, 1, -1), l'expression de l'intensité est assez lourde...
Je me demande si le concepteur de cet énoncé a bien mesuré la lourdeur des calculs dans le cas général. Presque toujours dans le cas de trois sources ou plus, on étudie la figure d'interférence à l'infini et non pas sur un écran situé à la distance D, même avec D très grand devant a. Cette observation s'obtient très simplement en observant la figure d'interférence dans le plan focal image d'une lentille convergente. Le schéma du dispositif est alors celui de la figure page 17 de ce document : ![]()
Cela dit, je veux bien t'aider à obtenir la différence de marche dans le cas de ta figure. Tu comprendras mieux le contenu de ce message ensuite !
Alors j'ai trouvé  1 = S1H = a*sin(
1 = S1H = a*sin( ).
).
Donc  2 =
2 =  1 ?
1 ?
Par rapport à a2/ D, il n'y a aucune précision. J'avoue ne pas trop avoir compris la suite de votre message Vanoise .
D, il n'y a aucune précision. J'avoue ne pas trop avoir compris la suite de votre message Vanoise .
Merci de votre aide.
Avec sin( )
) x/D...
x/D...
C'est très probablement la méthode attendue par ton professeur même si elle n'est pas très rigoureuse. Avec cette approximation, tu arrives à quelque chose de très simple. En choisissant la phase initiale de l'onde n° 2 en M égale à zéro, tu obtiens une somme très simple :
y2=a.cos( .t)
.t)
y1=a.cos( .t+
.t+ )
)
y3=a.cos( .t-
.t- )
)
Pour te convaincre qu'il s'agit bien d'une approximation, tu peux considérer le cas particulier x=0. La théorie simplifiée conduit à trois ondes en phases dans ce cas. Pourtant en réalité : les ondes 1 et 3 sont en phase car dans ce cas : d1=d3 mais l'onde n° 2 n'est pas en phase avec les deux autres car d2=D d1...
d1...
Ton schéma de 19h42 est rigoureux seulement si les trois rayons sont parallèles, donc si la figure d'interférence est étudiée à l'infini. Mais bon : retiens cette remarque car elle te sera utile quand tu étudieras les réseaux mais utilises la méthode simplifiée dont j'ai parlée dans le message précédent.
Pour illustrer mon propos sur l'approximation consistant à considérer les rayons comme parallèles avec D=3m alors que cela n'est rigoureux que pour l'écran rejeté à l'infini :
Comme déjà expliqué à 19h59 la solution très probablement attendue par ton professeur consiste à considérer D suffisamment grand devant "a" pour considérer les rayons émis par les trois sources en direction de M pratiquement parallèles. Cela conduit à considérer les différences de marches nulles entre les trois ondes et donc y1,y2 et y3 en phase dans le cas particulier x=0.
Si on fait le calcul rigoureux de la différence de marche entre l'onde 1 et l'onde 2 dans le cas particulier x= 0, on trouve :
Cette valeur est bien sûr "petite" puisque D>>a mais cette valeur est-elle négligeable devant la longueur d'onde ? En choisissant une longueur d'onde de 0,6µm, on obtient :
, ce qui est loin d'être négligeable ! Un raisonnement rigoureux consiste à exprimer les trois distances d1,d2 et d3 à l'aide du théorème de Pythagore puis à faire un développement limité pour simplifier, sachant que a<<D et |x|<<D. C'est tout à fait possible mais un peu long et sans doute pas demandé ici.
Bonjour,
Je trouve plutôt 0,05625, mais j'ai peut-être fait une erreur d'un facteur 100 quelque part.
C'est moi qui ai fait l'erreur d'un facteur 100. Merci gts2 !
Dans ce cas bien sûr, la méthode approchée expliquée précédemment dans mon message de 19h59 est acceptable. Tant mieux car elle est relativement simple.
Bonjour,
alors du coup si j'ai bien compris je dois additionner les trois ondes :
y = y1 + y2 + y3 = a ( cos( t) + cos(
t) + cos( t+
t+ ) + cos(
) + cos( t -
t -  ))
))
après je ne suis pas sur de la formule de cos à utiliser
y = a ( cos( t) + 2 cos(
t) + 2 cos( t)cos(
t)cos( ))
))
J'ai utiliser la formule cos(a+-b) = cosacosb +- sinasinb .
Je trouves donc : y = a cos( t) ( 1 + 2cos(
t) ( 1 + 2cos( )) .
)) .
Est ce correcte ?
J'ai bien compris que c'est une approximation vu que on ne le fais pas sur l'infini, mais en effet pour l'exo je penses qu'on peut considérer les trois droites // .
Juste une remarque : puisque l'intensité est proportionnelle au carré de l'amplitude :
I(x)=k.a2.[1+2cos( )]2 avec k : constante positive.
)]2 avec k : constante positive.
Ton énoncé, tel que tu l'as copié, n'est pas très clair sur la définition de Io. Certains auteurs posent : Io=k.a2, ce qui conduit à la formule que tu as obtenue, d'autre définissent Io comme l'intensité maximale et posent donc : Io=9k.a2.
Dans le résultat final, il faut remplacer  par son expression en fonction de x, a, D et
par son expression en fonction de x, a, D et  .
.
D'accord merci pour I(x)
Mais du coup pour cet exercice vaut il mieux poser d'après vous I0 = ka2 ou I0 = 9 * ka2 ?
Pour  je trouve (2*
je trouve (2* * ax) /
* ax) /  D
D
est ce correcte ?
De la meme maniere jai trouvé I'(x) = 4*a2cos( )2 = I0cos(
)2 = I0cos( )2 avec I0= 4*a2.
)2 avec I0= 4*a2.
Pour la dernière question pourriez vous m'indiquer la démarche à suivre pour réaliser le graphe ?
Merci d'avance
On notera I0 l'intensité
Manque de précision évident ! Manque peut-être l'adjectif "maximale" ?
Quoi qu'il en soit, si tu précises clairement sur ta copie, la signifie précise que tu donnes à Io puis fournis un résultat cohérent avec cette définition, ton professeur ne pourra qu'approuver !
J'ai vérifié au cas ou que je ne me sois pas tromper en recopiant mais il n'y a aucun adjectif maximal ou similaire.
J'avoue ne pas avoir très bien compris la partie 2 de votre réponse, il faut que j'explique qu'est ce que I0 ?
Concernant ton message de 13h20 : d'accord avec ton raisonnement. Cependant, pour pouvoir mieux comparer les deux courbes à la question 3, je pense qu'il faut garder à Io la même définition qu'à la question précédente : soit k.a2, soit 9k.a2. Avec deux sources plutôt que 3, il est logique d'obtenir une intensité maximale plus faible. De plus, de façon générale, le même symbole (ici Io) ne doit pas avoir deux significations différentes dans un même problème.
Pour les courbes :
puisque , étudier x pour
revient à étudier
 pour
pour . Pour les deux courbes, tu peux calculer I(x) et I'(x) pour
 variant par multiples de
variant par multiples de  /4 donc pour x variant par multiples de
/4 donc pour x variant par multiples de . Ayant placé tous ces points, tu termines par un tracé à « main levée » sachant qu'il s'agit de deux sinusoïdes. Évidemment, une calculatrice graphique où un logiciel scientifique sur ordinateur peut aider...
Pourquoi cette brutale multiplication par deux ?
 a été défini dans mon message du 04-12-20 à 19:59 comme le déphasage entre l'onde n° 1 et l'onde n° 2 et aussi le déphasage entre l'onde n°2 et l'onde n° 3.
a été défini dans mon message du 04-12-20 à 19:59 comme le déphasage entre l'onde n° 1 et l'onde n° 2 et aussi le déphasage entre l'onde n°2 et l'onde n° 3.
Tu as écris toi-même son expression dans ton message du 05-12-20 à 12:31, expression que j'ai validée et reprise dans mon message précédent.
Bien sûr, on peux dire que le déphasage entre l'onde n° 1 et l'onde n°3 vaut mais ce déphasage est noté 2
 et non
et non  ... ???
... ???
En fait j'ai voulu recalculer  pour 1 et 3 puis apres
pour 1 et 3 puis apres  mais je me suis trompé et comme vous l'avez dis ce n'est pas nécessaire vu qu'on a déjà
mais je me suis trompé et comme vous l'avez dis ce n'est pas nécessaire vu qu'on a déjà  .
.
Mais du coup,  a été définis comme le déphasage entre l'onde 1 et 2 puis l'onde 2 et 3, mais pas de l'onde 1 et 3 , si ?
a été définis comme le déphasage entre l'onde 1 et 2 puis l'onde 2 et 3, mais pas de l'onde 1 et 3 , si ?
Bonjour à tous,
En marge de cet exo et de ce document très intéressant sur les interférences (du 04-12 à 19h17), une question sur les chemins optiques :
- Supposons que la source Laser S émette un onde polarisée selon un axe fixe ; les plans d'onde sont tous perpendiculaires à cet axe et donc tous les points d'un même plan d'onde sont en phase les uns par rapport aux autres ;
- Prenons 3 points quelconques, S', S'',S''' d'un tel plan : sauf erreur, le chemin optique entre S et S', soit (SS') c'est n*SS' ; entre S et S'' c'est n*SS'' et entre S et S''' c'est n*SS''' ;
- Si les distances ne sont pas égales, ils ne seront pas égaux ni ne diffèreront d'un nbre entier de longueurs d'onde ; pourtant ils sont en phase :
Comment expliquer cela ?
Merci d'avance
Suppose un faisceau de lumière parallèle monochromatique, assimilé à une onde plane éclairant un ensemble de trous ou éventuellement de fentes si les symétries du dispositif le permettent. Si les différentes sources n'appartiennent pas à un même plan d'onde, les sources ne sont pas en phase. Cependant, les déphasages entre ces différentes sources ne varient pas au cours du temps. Les sources sont donc cohérentes et conduisent à un phénomène d'interférence.
Cette situation se rencontre en particulier dans le cas d'un réseau éclairée par une onde plane sous une incidence autre que normale. Pour en faire l'étude théorique, on peut reprendre le problème étudié ici et passer de 3 sources à N sources.
Bonjour Vanoise,
Merci pour la réponse, je comprends ces explications ;
Pour en revenir à cette notion de chemin optique, je dirais qu'entre 2 plans d'onde d'un faisceau Laser de lumière parallèle, ces 2 plans sont parallèles, les chemins optiques sont nécessairement perpendiculaires à ces 2 plans, donc parallèles entre eux et égaux.
- Autre façon de dire : entre 2 tels plans d'onde, la lumière ne peut pas suivre un trajet oblique,
Cordialement
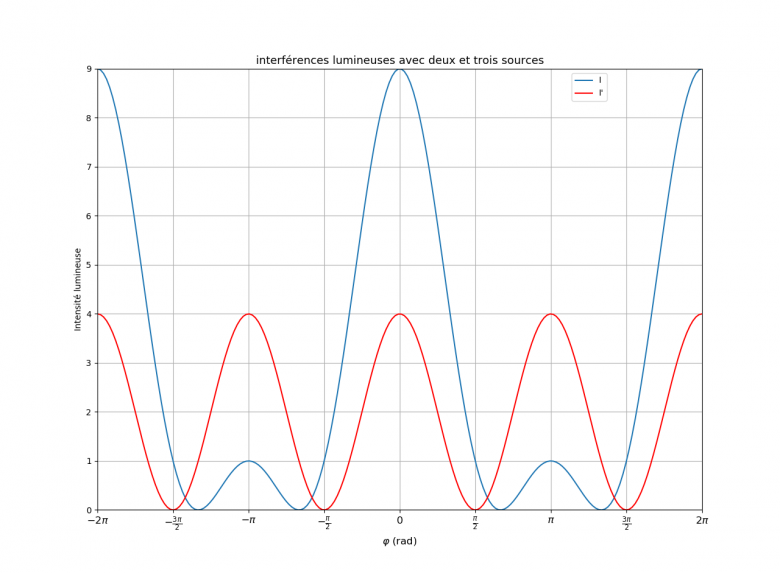
Chimival ,'a pas poster les courbes I=f(x) (trois sources) et I'=g(x) (deux sources).
Voici le résultat. J'ai laissé en abscisses les valeurs de  . Facile de convertir en abscisses x sachant que :
. Facile de convertir en abscisses x sachant que : .
Merci pour ces compléments,
Au cas où il n'y aurait plus qu'une seule source, il n'y aurait plus d'interférences mais la droite I = Io =1, non ?
Dans ce contexte, une seule source ne permet pas d'obtenir un phénomène d'interférence, ce qui conduit effectivement à I=constante.
Attention cependant : en réalité, le phénomène de diffraction fait que I n'est pas rigoureusement indépendant de x sauf à imaginer une fente infiniment fine mais une fente infiniment fine ne laisse pas passer la lumière. L'étude précédente suppose donc implicitement les fentes suffisamment fines pour que la partie de l'écran où le phénomène d'interférence est étudié : appartienne à la partie centrale de la tache principale de diffraction.


