Inscription / Connexion Nouveau Sujet
Exercice sur les moments par rapport à un axe
 leprof001
leprof001Bonjour,
Je suis nouveau sur le forum et j'ai une préoccupation en statique.
Ma question est de savoir :
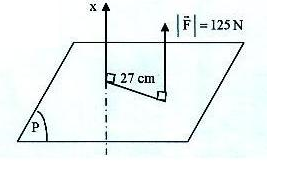
1. Comment calculer le moment de F par rapport à l'axe x ?
(Dans ma recherche de solution, j'ai trouvé que ce moment est nul car nous nous trouvons en face de 3 vecteur qui détermine un plan différent du plan P - cela, d'après les propriétés de cette relation)
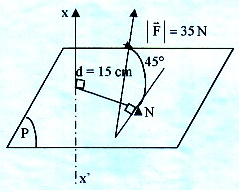
2. Quel sera ce même moment si on incline F de 45° par rapport au plan P ?
(Ici, je suis perdu...)
Merci de votre aide.
Bonjour.
Le moment par rapport à un axe est nul si la force est dirigée parallèlement à l'axe (le moment est aussi nul si la force est dirigée par une droite qui coupe l'axe).
Lorsque la force est inclinée de 45°, on peut la décomposer en une force orthogonale à l'axe, et une force parallèle, et utiliser la linéarité du moment, c'est-à-dire M(F1+F2)=M(F1)+M(F2).
La composante parallèle a un moment nul, tandis que pour l'autre on peut utiliser la formule du bras de levier : M= dF, où d est la distance entre le point le plus proche de la droite qui porte F et l'axe, et F la norme de F, attention ici ce ne sera pas 125N, mais plutôt la norme de la composante orthogonale à l'axe, qui est donc inférieure.
dF, où d est la distance entre le point le plus proche de la droite qui porte F et l'axe, et F la norme de F, attention ici ce ne sera pas 125N, mais plutôt la norme de la composante orthogonale à l'axe, qui est donc inférieure.
Pour savoir si l'on met un + ou un -, le moment est positif si la force entraîne un mouvement dans le sens trigonométrique.
Re bonsoir,
"Le moment par rapport à un axe est nul si la force est dirigée parallèlement à l'axe (le moment est aussi nul si la force est dirigée par une droite qui coupe l'axe)".
Pouvez vous me dire comment justifier cela ?
Mais avant, je souhaiterais savoir si le raisonnement que j'ai adopté est juste ?
Si oui, je voudrais approfondir le sujet de l'exercice pour dire :
Si l'axe de rotation n'était pas perpendiculaire au plan P, nous aurions utilisé la relation du produit mixte de 3 vecteur. Quelle est alors la valeur du vecteur unitaire de l'axe ?
Où pourrais je avoir un document qui me parle de long en large de ce sujet (Moment par rapport à un axe)
merci
j'ai trouvé que ce moment est nul car nous nous trouvons en face de 3 vecteur qui détermine un plan différent du plan P - cela, d'après les propriétés de cette relation
En toute franchise, je n'ai pas très bien saisi le raisonnement.
"Le moment par rapport à un axe est nul si la force est dirigée parallèlement à l'axe (le moment est aussi nul si la force est dirigée par une droite qui coupe l'axe)".
Pouvez vous me dire comment justifier cela ?
Notons
1er cas : La force est dirigée parallèlement à l'axe, donc la force est dirigée par
Le moment vaut :
Les coordonnées cylindriques semblent adaptées au problème, alors en notant
Donc :
Or par définition du produit vectoriel, on est en train de faire le produit scalaire entre
Raisonnement similaire pour
Merci WilliamM007
pour ton raisonnement et pour le travail abattu.
Et maintenant pour le deuxième volet du problème
(Quel sera ce même moment si on incline F de 45° par rapport au plan P ? )
à bientôt
Tout dépend de la manière dont on l'incline. 45° ça peut être dans toutes les directions.
En fait j'ai déjà répondu à la question plus haut, en prenant le cas où l'on incline de 45° de telle sorte qu'une composante soit parallèle, et une autre composante soit dirigée selon le vecteur orthoradial des coordonnées cylindriques.
Par contre, si l'on incline de 45° en faisant un angle de 45° avec l'axe, alors on se retrouve avec une composante parallèle à l'axe, et une composante dont le prolongement coupe l'axe, on reconnaît deux cas où le moment s'annule et le moment est nul.
Donc cela dépend de la manière d'incliner. La question est très ambiguë.
D'accord.
Alors en fait il faut décomposer la force .
Notons la base cylindrique.
Remarquons que
Autrement dit, a une composante parallèle à l'axe, et une composante orthoradiale.
La composante parallèle, on a montré qu'elle est nulle.
Quant à la composante orthoradiale, on applique le bras de levier :
M= d*F, où M est le moment par rapport à l'axe, d la distance entre la composante orthoradiale et l'axe, et F l'intensité de la composante orthoradial de la force.
d*F, où M est le moment par rapport à l'axe, d la distance entre la composante orthoradiale et l'axe, et F l'intensité de la composante orthoradial de la force.
Ici, d=15cm, et F= (35/2)N.
(35/2)N.
Comment savoir si l'on met un signe + ou - ? Si la force encourage un mouvement dans le sens trigonométrique, c'est un +, sinon c'est un -.
Preuve de la technique du bras de levier :
Ici, on met seulement à droite du produit vectoriel car on sait que le calcul d'une composante parallèle nous conduit à un moment nul.
Analysons un peu ce produit. À gauche, il y a entre autres , qui va donc donner un vecteur orthogonal à
, or il faut après faire un produit scalaire avec
, donc le résultat sera nul.
Ainsi, le moment vaut finalement :
On voit facilement que cela donne : , où d est la distance entre la composante orthoradiale et l'axe, qui ici vaut 15cm, et F l'intensité de la composante orthoradiale, qui ici vaut
 (35/2)N.
(35/2)N.
sin(T) vaut 1 si le trièdre (r,t,z) est direct, ce qui revient à dire que entraîne un mouvement dans le sens trigonométrique. Sinon, sin(T)=-1.
WilliamM007 je voudrais te demander une dernière chose; peux tu m'indiquer un doc sur le net qui parle exclusivement de produit mixte de 3 vecteurs (sous forme géométrique et analytique)?
merci d'avance