Inscription / Connexion Nouveau Sujet
Exercice RDM
Bonjour tout le monde, je suis bloqué au niveau de ce exercice surtout, si quelqu'un peut m'aider, merci d'avance.
voila l'énonce de l'exercice :
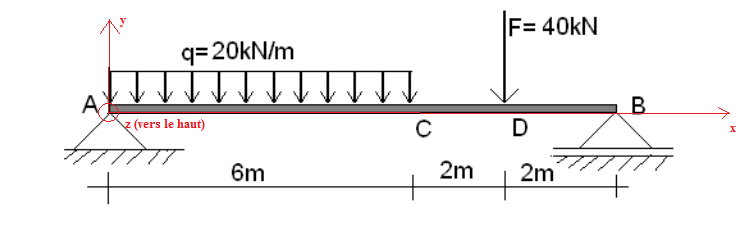
Soit la poutre montrée sur la figure ci-dessous.
1- Calculer les torseurs des forces F et q par rapport aux points A, B, C et D.
2- Etudier l'équilibre de cette poutre.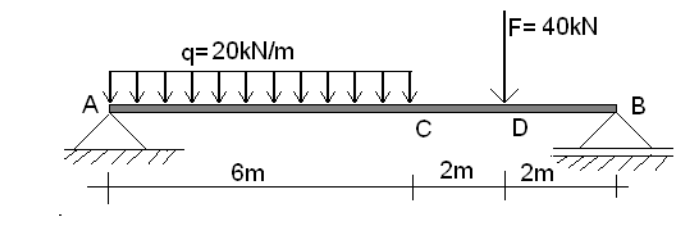
Bonjour,
Je te souhaite la bienvenue sur le forum.
Pour mémoire :
Aider ne veut pas dire faire, on s'attend en effet à avoir des pistes de réflexion sur lesquelles échanger avec toi
J'attends donc tes pistes pour pouvoir démarrer,

Mon cours dit :
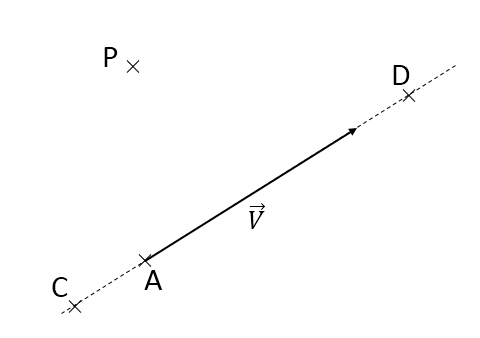
Moment d'un vecteur par rapport a un point est :
Mp=PA vectoriel V
=PD vectoriel V
=PC vectoriel V
Me revoici !
Je te propose de commencer par étudier la force dans le repère (A, x, y, z)
Quelles sont les composantes de cette force dans ce repère ?
Quel est son torseur en D ?
Comment écrire ce torseurs à d'autres points ?

Bonjour,
S'il-te-plaît, évite de poster tes propositions les unes à la suite des autres, ça alourdit la lecture de ton sujet  .
.
Concernant tes propositions :
On peut même ajouter que Fz = 0 car j'ai précisé qu'on avait un repère à 3 dimensions.
Au point D:
Au point C:
Au point A:
Au point B:
Tout en rappelant que l'unité de chaque moment est kN.m
Concernant la charge répartie q, tu dois avoir une formule dans ton cours qui doit t'expliquer comment appréhender celle-ci.
Ta résultante sera effectivement une force dont il faut préciser son point d'application.
Concernant le calcul du moment, la méthode analytique va être un peu plus difficile. Tu peux t'aider du schéma car une méthode schématique est plus aisée.

On remplace la charge repartie par une force équivalente tel que :
Torseur au point A :
Torseur au point B :
Torseur au point C :
Torseur au point D :
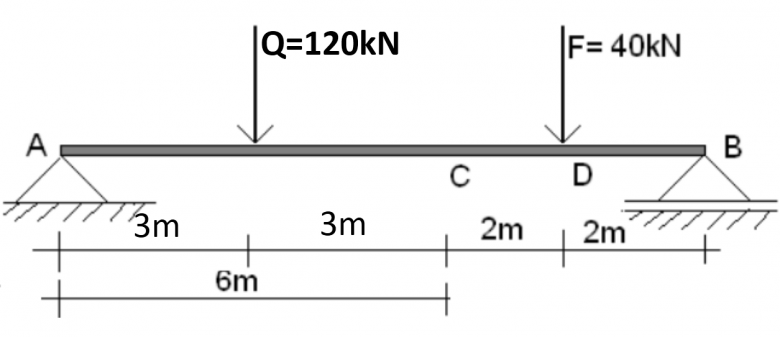

N'oublie pas de préciser que tes moments sont suivant l'axe (Oz) donc suivant
OK merci

comment on va étudier l'équilibre de la poutre ?
Quelles sont les deux conditions qui traduisent un équilibre ?
Somme des résultantes = vecteur nul
Somme des moment en un point = vecteur nul.

Tu modélises effectivement les efforts générés par tes appuis en A (probablement Xa et Ya) et en B (probablement Xb et Yb) puis tu traduis l'équilibre :
* via l'équation de la résultante statique en projection suivant l'axe (Ax) ;
* via l'équation de la résultante statique en projection suivant l'axe (Ay) ;
* via l'équation de moment en un point judicieusement choisi (pour supprimer des inconnues) suivant (Az) : en A ou en B, au choix.

Tu as vu en cours le principe fondamental de la statique (ou première loi de Newton) ?
Si je reprends ton schéma :
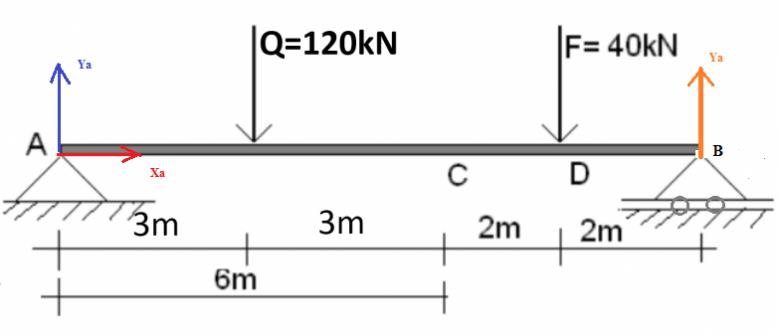
* Equation de la résultante statique en projection suivant l'axe (Ax) :
Xa = 0 (équation 1)
* Equation de la résultante statique en projection suivant l'axe (Ay) :
Ya - Q - F + Yb = 0 (équation 2)
* Equation de moment en un point judicieusement choisi (pour supprimer des inconnues) suivant (Az) : faisons -le en A par exemple :
0 - 3*Q - (3 + 3 + 2)*F + (3 + 3 + 2 + 2)*Ya = 0 (équation 3)
<=> Ya = ?
Puis on injecte la valeur trouvée pour Ya dans l'équation 2, ce qui nous permet d'en déduire Yb

Tu t'en sors ?
Je n'ai fait que définir les inconnues au niveau des appuis en A et B et utiliser ton travail du 09-06-20 à 14:20

Oui !
Sinon exprimer les 3 équations sans les utiliser c'est dommage.

Merci beaucoup, je vous suis reconnaissant



Je t'en prie  !
!
Je te fais confiance pour les valeurs.
Un bon moyen pour vérifier que c'est correct c'est d'injecter ces valeurs dans l'équation 2 écrite précédemment et de s'assurer qu'on retrouve un résultat nul 
Je t'en prie
 !
!
Je te fais confiance pour les valeurs.
Un bon moyen pour vérifier que c'est correct c'est d'injecter ces valeurs dans l'équation 2 écrite précédemment et de s'assurer qu'on retrouve un résultat nul

Oui, c'est juste
Merci


 moteur de recherche
moteur de recherche page de choix du forum
page de choix du forum fiches du site
fiches du site