Inscription / Connexion Nouveau Sujet
Exercice physique : roulement sans glissement
Bonjour j'ai un petit problème avec un exercice pourriez vous m'aider?
L'exercice est constitué de 3 parties les 2 premières sont faciles:
3. Un cercle de rayon R et de centre I roule sans glisser sur l'axe (Ox) avec une vitesse angulaire .
On étudie le mouvement du point M du cercle qui coïncide avec O à l'instant t=0
a- Déterminer les coordonnées cartésiennes de M à l'instant t. Quelle est la nature de la trajectoire ? (Fait)
b- En déduire le module du vecteur position , et calculer les vecteurs de la base polaire en fonction de la base cartésienne.
c-Calculer les vecteurs vitesse et accélération dans la base des coordonnées polaires. En déduire les modules .
d- Déterminer les composantes tangentielles et normales de l'accélération et le rayon de courbure
C'est surtout la question b que je n'ai pas réussi à résoudre .Le reste des questions semblent simples.
***Edit gbm :
- titre changé pour plus de clarté ;
- niveau mis en accord avec ton profil***
Bonjour,
J'ai déjà eu l'occasion d'aider quelqu'un sur le même sujet. Commence par regarder les messages suivants (l'aide est graduée et s'effectue sur trois messages successifs) :
Devoir coordonnées polaires
Si tu as des questions complémentaires, n'hésite pas !
vanoise stp peux tu ajouter sur ton shema les vecteurs 
t et n car comme moi j'ai commencé avec Une position totalement différente de M je ne me retrouve plus avec les angles
Merci encore pour ton aide
Bonsoir,
Les vecteurs unitaires de Frénet ne sont pas déduits de simples projections mais calculés à partir de leurs définitions rappelées dans mon message du 12-11-15 à 00:33 : le vecteur unitaire Ut est tangent à la trajectoire donc colinéaire au vecteur vitesse. Le vecteur Un est orthogonal au précédent et orienté vers l'intérieur de la trajectoire ; on peut le définir à partir d'un produit vectoriel, le vecteur unitaire Uz étant normal au plan de figure et orientée vers l'avant de celle-ci. Voici la figure complétée : attention tout de même : j'ai représentée seulement "l'allure générale" de la trajectoire : mon logiciel de dessin ne permet pas de tracer une cycloïde de façon précise.
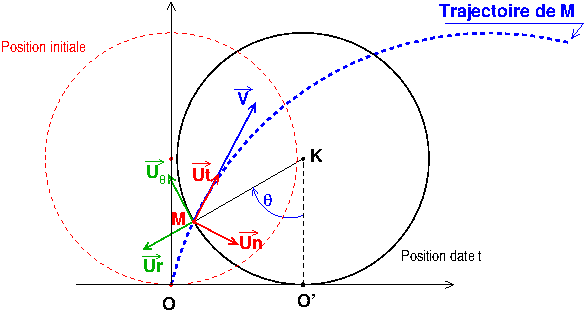
Merci bcp pour ton aide cependant j'ai une dernière question est tu sûr du sens du vecteur 
?
Car notre prof nous a montré une astuce pour ça (la main droite ) et Ça ne coïncide pas avec le schéma , corrige moi si je me trompe stp
J'imagine que l'astuce dont tu parles concerne les situations où le sens positif de rotation est le sens trigonométrique (sens antihoraire). Dans ce problème, le sens positif de rotation est le sens horaire.... Mais tout cela est simplement une affaire de notation arbitraire : il suffit que les raisonnement et les calculs soient cohérents avec les sens et les vecteurs unitaires choisis.
?
Annuler
connectez vous