Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Exercice : Forces centrales

Posté par
student123 08-11-16 à 13:31

Salut
S'il vous plaît j'ai besoin d'aide pour cet exercice,  je ne sais pas d'où commencer .
On transfert un satellite de masse m=1000kg d'une orbite circulaire de rayon r1 du centre de la terre sur son orbite définitive géostationnaire à la distance r2, ce transfert se fait en deux  étapes: -On fait varier brusquement et tangentiellement la vitesse du satellite ce qui lui imprime une orbite elliptique dite de transfert .
-Au passage à L'apogée de l'orbite de transfert on fait varier brusquement et tangentiellement la vitesse du satellite  pour Lui donner son orbite circulaire définitive
1) Calculer l'énergie qu'il faut fournir instantanément pour passer de l'orbite circulaire(r1)à l'orbite elliptique et déduire la variation de sa vitesse  correspondante
2) Calculer le temps de transfert t1
3) Calculer l'énergie qu'il faut transférer au satellite pour passer(r1)à(r2)



Merci beaucoup !

Posté par
vanoisere : Exercice : Forces centrales 08-11-16 à 18:41

Bonsoir
Et si tu commençais par expliquer ce que tu as été capable de faire et par poser des questions précises sur ce que tu ne comprends pas ? L'aide apportée ensuite sera plus efficace !
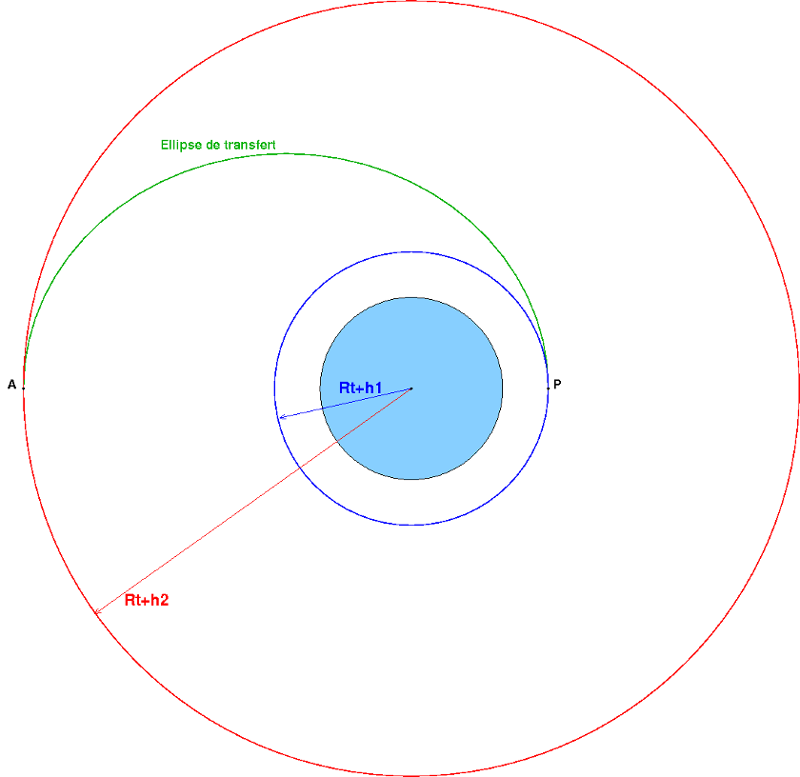
Pour t'aider un peu : voici un schéma fait il y a quelque temps pour aider quelqu'un d'autre (adapte les notations si nécessaire).

Exercice : Forces centrales

Posté par
student123re : Exercice : Forces centrales 08-11-16 à 18:51

Bonsoir
Je bloque dans la première question,  Em=1/2 m v^2 -(GMm)/r1
Je me demande si v = v1 ? Qui est la racine de GM/r1..
Et pour la variation de la vitesse  je dérive l'énergie  mécanique ?
Merci pour votre aide.

Posté par
vanoisere : Exercice : Forces centrales 08-11-16 à 19:18

L'étude du mouvement circulaire de rayon r1 te permet de calculer la vitesse du satellite sur l'orbite "bleue". En P, la vitesse doit varier de façon de devenir la vitesse correspondant au périgée de l'orbite de transfert "verte". Connaissant r1 et r2 tu peux déterminer les caractéristiques de cette ellipse de foyer située au centre de la terre ; tu pourras alors calculer la vitesse en P puis en A. Ensuite, la vitesse doit à nouveau varier pour devenir cele correspondant à l'orbite circulaire "rouge".
Tu dois sûrement avoir un cours structuré sur le sujet. A défaut, tu peux consulter la fiche n° 8 que j'ai eu l'occasion de rédiger sur ce sujet :
La dernière partie en particulier devrait t'aider ; pour la première partie, il n'est pas certain que les formules de Binet soit à ton programme...

Posté par
student123re : Exercice : Forces centrales 08-11-16 à 19:42

Merci pour votre aide.
Voilà ce que j'ai trouvé:
1)
Em = -GmM/(r1 + r2)
Et la vitesse  est la racine de 2 (Em + GMm/r1)
2)
T est la racine de 4 pi^2 . a^3 / GM
3) Em = - GmM/2r2
Je me demande si c'est correct ?

Sinon pour les formules de Binet on les a vu au cours mais vont ils nous servir dans cet exercice ?

Posté par
vanoisere : Exercice : Forces centrales 08-11-16 à 20:43

Commence déjà par exprimer les vitesses correspondant aux 2 trajectoires  circulaires de rayons r2 et r1. Ensuite déduits de r1 et r2 les paramètres de l'ellipse de transfert . Ensuite determine les vitesses à l'apogée et au perigée de celle ci. Le site indiqué devrait t'aider pour l'ellipse.

Posté par
student123re : Exercice : Forces centrales 08-11-16 à 21:57

les vitesses à l'apogée et au perigée  ne sont elles pas celles de r2et r1 ?
Sinon on a 2a = r1 + r2 et Em = -k/2a avec k = gmM
d'où:
1)
Em = -GmM/(r1 + r2)
Et la vitesse  est la racine de 2 (Em /m+ GM/r1)  ou bien la racine de GM(2/r1 - 1/a)
2)
T est la racine de 4 pi^2 . a^3 / GM
3) V2=(V1 . r1)/r2 ou bien v2 = racine de GM(2/r2 - 1/a)
et Em = 1/2 m(v2)^2 - GMm/r2
Je me demande si ce n'est pas correct ?
Merci

Posté par
vanoisere : Exercice : Forces centrales 09-11-16 à 09:57

Bonjour
Il s'agit de calculer la variation d'énergie et la variation de vitesse qu'il faut créer en P puis en A.
Tu alignes des formules sans les justifier. Essaie d'être précis dans tes réponses :
1 : énergie mécanique en P si orbite circulaire : ....
2 : énergie mécanique en P si trajectoire elliptique : ...
3 : variation d'énergie cinétique en P : ...
4 : variation de vitesse en P : ....

Même chose ensuite en A...
Il ne s'agit pas d'aligner des formules de cours sans aucune justification...
Je te laisse réfléchir ...

Posté par
student123re : Exercice : Forces centrales 09-11-16 à 15:57

Bonjour
Je vais essayer d'être plus précis:
1 : énergie mécanique en P si orbite circulaire :

Em1 = \frac{1}{2}mv_{1}^{2} - \frac{GMm}{r1}

Em1 = - \frac{GMm}{2r1} car v_{1}^{2}= \frac{GMm}{r1}

2 : énergie mécanique en P si trajectoire elliptique :

Em2=\frac{-GMm}{2a} avec a =r1+r2 ( je pense que je n'ai pas besoin de  justifier cette formule (?) )
Et on a Em2= \frac{1}{2}mv_{2}^{2}-\frac{GMm}{r1}

3 : variation d'énergie cinétique en P :
Em2-Em1= \frac{1}{2}mv_{2}^{2} - \frac{1}{2}mv_{1}^{2} =Ec2-Ec1=Ec

alors Ec = \frac{-GMm}{r1+r2} + \frac{GMm}{2r1}

Ec = \frac{GMm(r2 - r1)}{2r1(r1+r2)}
4 : variation de vitesse en P :
v =2\frac{Ec}{m} = \frac{GM(r2 - r1)}{r1(r1+r2)}
1 : énergie mécanique en A si orbite circulaire : ....
EmA1 = - \frac{GMm}{2r2}
2 : énergie mécanique en A si trajectoire elliptique :
\frac{-GMm}{2a}
Et on a aussi  EmA2= \frac{1}{2}mv_{2}^{2}-\frac{GMm}{r2}

3 : variation d'énergie cinétique en A : ...
EcA=EmA1-EmA2= \frac{1}{2}mv_{a1}^{2} - \frac{1}{2}mv_{a2}^{2}
EcA=\frac{-GMm}{2r2}+\frac{GMm}{2a}
EcA = \frac{-GMm (r2-r1)}{2r2(r1+r2)}

4 : variation de vitesse en A : ....
v =2\frac{Ec}{m} = \frac{GM(r1 - r2)}{r2(r1+r2)}
Sinon comment faire pour calculer le temps de transfert t1 ? t1 = T2 - T1 ?
Merci  pour votre aide.

Posté par
vanoisere : Exercice : Forces centrales 09-11-16 à 16:17

Voilà qui est particulièrement clair et précis et en plus : tu fais l'effort d'utiliser l'éditeur d'équation pour une meilleure lisibilité ! Bravo !
Le temps de transfert est égal à une demie période du mouvement elliptique. La troisième loi de Képler va te fournir le résultat.

Posté par
student123re : Exercice : Forces centrales 09-11-16 à 16:22

Merci beaucoup pour votre aide  

Posté par
J-Pre : Exercice : Forces centrales 09-11-16 à 19:22

Le calculs des variations de vitesse me semble bien hasardeuses.

Tes équations ne sont pas homogènes

Voila ce que je trouve (pas vérifié) pour ce qui se passe en P

1)

Em1 = -GmM/(2.r1)

Em2 = -GmM/(2.(Rt + h2 + Rt + h1)) = -(GmM)/(r1+r2)


Delta Em = Em2 - Em1

Delta Em = - (GmM)/(r1+r2) + (GmM)/(2r1)

Delta Em = (GmM). (r1+r2-2r1)/((2r1.(r1+r2))

Delta Em = (GmM). (r2-r1)/((2r1.(r1+r2))

En P, l'énergie potentielle est la même pour les 2 orbites -->

Delta Ec = (GmM). (r2-r1)/((2r1.(r1+r2))  
-----

Sur orbite circulaire : Ec1 = GmM/(2.r1)

GmM/(2.r1) = 1/2.m.V1²
V1 = RC[GM/R1]

Ec2 = Ec1 + Delta Ec

Ec2 = (GmM). (r2-r1)/((2r1.(r1+r2)) + GmM/(2.r1)

Ec2 = GmM/(2.r1) * [(r2-r1)/(r1+r2) + 1]

Ec2 = GmM/(2.r1) * [2.r2/(r1+r2)]

Ec2 = GmM. r2/[r1.(r1+r2)] = 1/2.m.v2²

V2² = 2.G.M. r2/[r1.(r1+r2)]

V2 = RC[2.G.M. r2/(r1.(r1+r2))]

Delta v = v2 - v1

Delta v = RC(GM/r1) * [RC(2.r2/(r1+r2)) - 1]

C'est la variation de vitesse en P

Et là, c'est tout à fait différent de ton résultat.
-----

Il y a sans aucun doute, plus direct ... mais soit.

Sauf distraction.  

Posté par
J-Pre : Exercice : Forces centrales 09-11-16 à 19:23

Désolé pour l'orthographe.  

Posté par
student123re : Exercice : Forces centrales 09-11-16 à 20:29

Tout d'abord, merci pour votre réponse.
Dans mon post précédent j'avais oublié la racine pour les vitesses. ^^'
Par contre je me demande si cette méthode est correcte pour trouver  deltav on la pose comme RC (2deltaEc/m))..
Sinon je comprends bien le calcul que vous avez fait.

Posté par
vanoisere : Exercice : Forces centrales 09-11-16 à 21:36

Bonsoir student123
Je t'ai félicité tout à l'heure pour la clarté de ton raisonnement et la lisibilité de tes formules. Tu as cependant commis quelques étourderies de calcul. Tout va bien jusqu'à la ligne 3 mais à la ligne 4, la variation d'énergie cinétique \varDelta Ec fait intervenir la variation du carré de la vitesse et non la variation de la vitesse. Ligne 4, il faut donc écrire :

\varDelta v^{2}=2\frac{\varDelta Ec}{m}=\frac{GM(r2-r1)}{r1(r1+r2)}=v_{2}^{2}-v_{1}^{2}=v_{2}^{2}-\frac{GM}{r_{1}}
Ce qui donne :

v_{2}^{2}=\frac{GM(r_{2}-r_{1})}{r_{1}(r_{1}+r_{2})}+\frac{GM}{r_{1}}=\frac{GM}{r_{1}}\cdot\frac{2r_{2}}{r_{1}+r_{2}}
La variation de vitesse est ainsi :

\boxed{\varDelta v=v_{2}-v_{1}=\sqrt{\frac{GM}{r_{1}}}\cdot\left(\sqrt{\frac{2r_{2}}{r_{1}+r_{2}}}-1\right)}
Tu as commis la même étourderie pour la variation de vitesse en A plus une autre dans le calcul de la variation d'énergie cinétique.

\varDelta E_{cA}=Em_{A2}-Em_{A1}=-\frac{GMm}{2r_{2}}+\frac{GMm}{r_{2}+r_{1}}=\frac{GM(r_{2}-r_{1})}{2r_{2}(r_{1}+r_{2})}

\varDelta v_{A}^{2}=2\frac{\varDelta Ec}{m}=\frac{GM(r_{2}-r_{1})}{r_{2}(r_{1}+r_{2})}=v_{A2}^{2}-v_{A1}^{2}=\frac{GM}{r_{2}}-v_{A1}^{2}

v_{A1}^{2}=\frac{GM}{r_{2}}-\frac{GM(r_{2}-r_{1})}{r_{2}(r_{1}+r_{2})}=\frac{GM}{r_{2}}\cdot\frac{2r_{1}}{r_{1}+r_{2}}

La variation de vitesse est ainsi :

\boxed{\varDelta v_{A}=v_{A2}-v_{A1}=\sqrt{\frac{GM}{r_{2}}}\cdot\left(1-\sqrt{\frac{2r_{1}}{r_{1}+r_{2}}}\right)}
La durée du transfert est la demie période du mouvement elliptique sur l'orbite de transfert :

\boxed{\varDelta t=t_{A}-t_{P}=\pi\cdot\sqrt{\frac{a^{3}}{GM}}=\pi\cdot\sqrt{\frac{r_{1}+r_{2}}{8GM}}}

puisque : 2a=r_{1}+r_{2}.

Posté par
vanoisere : Exercice : Forces centrales 10-11-16 à 11:31

Bonjour student 123
Un petit complément concernant la rapidité de la méthode. Pour l'étude en P : tu n'as pas le choix ; la méthode est imposée par l'énoncé. En revanche, plutôt que d'utiliser la même méthode en A, tu peux faire plus rapide en considérant la conservation du moment cinétique le long de la trajectoire elliptique. Le moment cinétique du satellite, calculé au centre O de la terre s'écrit :

\overrightarrow{L}=m\cdot\overrightarrow{OP}\wedge\overrightarrow{v_{2}}=m\cdot\overrightarrow{OA}\wedge\overrightarrow{v_{A1}}
Puisque vecteur position et vecteur vitesse sont orthogonaux à la fois en P et en A, cela donne très simplement :

r_{1}\cdot v_{2}=r_{2}\cdot v_{A1}

v_{A1}=\frac{r_{1}}{r_{2}}\cdot\sqrt{\frac{2GM\cdot r_{2}}{r_{1}\left(r_{1}+r_{2}\right)}}=\sqrt{\frac{2GM\cdot r_{1}}{r_{2}\left(r_{1}+r_{2}\right)}}
Puisque v_{A2} est la vitesse correspondant au mouvement circulaire de rayon r_{2}, le problème est terminé !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !