Inscription / Connexion Nouveau Sujet
Exercice en Théorème de Thévenin
Salut,
J'ai vraiment besoin de votre aide!
Voilà un exercice où on a besoin de l'application du théorème du Thévenin.
"L'énoncé :
1. En appliquant le théorème de Thévenin, évaluer le courant à travers la résistance de 2 ohm du circuit.
2. En appliquant le théorème de Thévenin, évaluer le courant à travers la résistance de 6 ohm du cricuit.
3. Vérifier l'équilibre du bilan des puissances sur ce circuit."
Au début je me qoince.
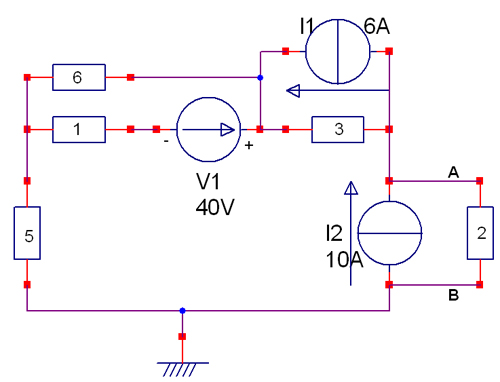
Tout d'abord, pour calculer la résistance équivalente , on doit cour-circuiter où se trouvent les générateurs de tensions et d'intensité.
Mais je n'arrive pas , pourtant, à la calculer.
J'ai vraiment d'aide!
Merci d'avance 
Ci-joint: Le circuit étudié
Tout d'abord, pour calculer la résistance équivalente , on doit cour-circuiter les générateurs de tensions et enlever les générateurs d'intensité.
Salut,
J'aimerais bien que ça soit étape par étape, si possible 
Voilà , je ne savais pas qu'on doit enlever les générateurs d'inténsité et non pas uniquament les courcircuiter.
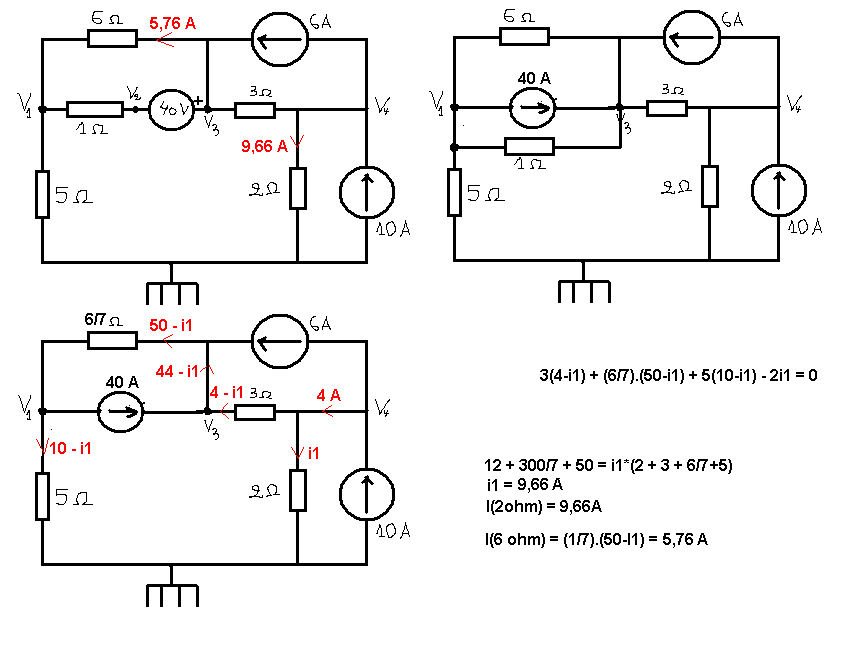
voilà ce que j'obtiens alors Rth = 3+6/(6+1)+5 = 62/7 ohms , comme le résultat d'Abdel01
Est'ce que le circuit est bien correcte?
pour calculer Eth tu n'as qu"as calculer la ddp dans la branche où se trouve la resistance(Va-Vb). mazis pour cela utilise le reseau initial
J'ai posté accidentellement...
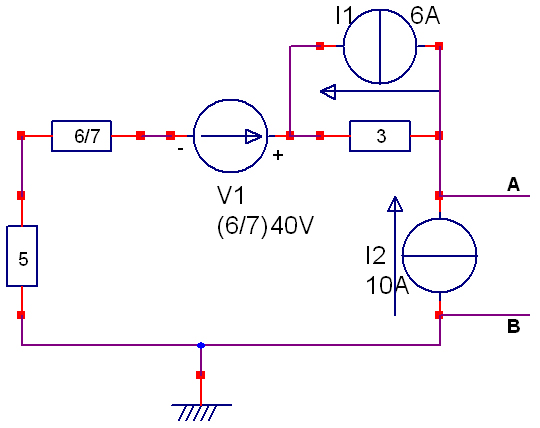
On peut commencer, bien que ce ne soit pas absolument nécessaire, par remplacer l'ensemble générateur 40 V, 6 ohms et 1 ohm par le générateur de Thévenin équivalent.
Ceci nous donne Eth = (6/7)40 et la Rth est 6  // 1
// 1  donc Rth = 6/7
donc Rth = 6/7  .
.
Ensuite on coupe aux points A et B. Pour trouver la résistance de Thévenin équivalente, on cherche la résistance entre A et B en éteignant les générateurs et en les remplaçant par leur résistance interne (0 pour les générateurs de tension et une résistance infinie pour les générateurs de courant).
Rth = 3 + (6/7) + 5 = 8 + (6/7)
comme cela a déjà été trouvé.
Après, on va s'occuper de Eth...
Le courant du générateur 10 A passe, d'une part par le générateur de courant de 6 A, et d'autre part par la résistance de 3  pour les 4 A qui restent. Ensuite on trouve (6/7)40 V et la résistance de 6/7
pour les 4 A qui restent. Ensuite on trouve (6/7)40 V et la résistance de 6/7  traversée par 10 A, puis la résistance de 5
traversée par 10 A, puis la résistance de 5  traversée par 10 A. Donc si on fait la somme :
traversée par 10 A. Donc si on fait la somme :
Eth = (4x3) + (6/7)40 + 10 6/7 + (5x10)
Eth = 734/7 V
on a donc:
Eth = (Rth+R)I
734/7 = (8 + 6/7 + 2)I
d'où : I = (734/7) (7/76)  9,66 A
9,66 A
Cela doit répondre à la question 1 : "En appliquant le théorème de Thévenin, évaluer le courant à travers la résistance de 2 ohm du circuit".
On pourrait aussi remplacer le générateur de 6 A et la résistance de 3  par le générateur de tension équivalent en appliquant le théorème de Norton. Mais cela n'amène pas de simplification déterminante...
par le générateur de tension équivalent en appliquant le théorème de Norton. Mais cela n'amène pas de simplification déterminante...
De la même façon...
Pour appliquer le théorème de Thévenin, je pense qu'il est plus facile de commencer à appliquer le théorème de Norton pour transformer les générateurs de courant en générateurs de tension.
Ensuite, on applique "bêtement" le théorème de Thévenin.
On calcule Eth aux bornes de la 6  (enlevée) et Rth, la résistance aux bornes de la 6
(enlevée) et Rth, la résistance aux bornes de la 6  (enlevée) avec les générateurs remplacés par leur résistance interne.
(enlevée) avec les générateurs remplacés par leur résistance interne.
ah merci je vois maintenant si non j ai un probleme pour calculer Eth avec l'exercice ci dessous
*** lien effacé ***
je trouve Eth = 3.6 alors qu on parle de 1.6 v
Edit Coll