Inscription / Connexion Nouveau Sujet
exercice electromag
Bonjour voici un exercice que je ne n''arrive pas a faire y aurait il qqn pour m'aider ? merci d'avance.
** énoncé effacé ; image laissée **
Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
![]() [lien]
[lien]
La Figure montre une tige fine, rectiligne, de longueur L et portant une densité de charge linéique p. Une charge q est placée au point P, sur la médiatrice de la tige à une distance h de son milieu O.
Chaque élément dx, placé à la distance r par rapport à P, porte une
r
charge (ro).dx et va exercer sur q une force proportionnelle à r/r^3*(q.(ro)).dx
La force totale devient : ftot=int( entre x1x2 )k.(q(ro).r)/r^3 dx
1) Donner sans la résoudre, l'expression de Fy la composante de FT,t suivant êy en fonction de r, teta et dx.
Pour résoudre cette équation un changement de variable(r;x)--teta est necessaire
2) Dans le triangle (0, P, x), exprimer r et x en fonction h et teta
3) A partir de l'expression de x, exprimer dx en fonction de h, teta et dû.
(Vous aurez besoin de la relation : d(tan(0)) = 1/ cos^2 teta
4) Effectuer le changement de variable en remplaçant x, r et dx par leurs valeurs dans l'expression obtenue au 1) et en déduire Fy en fonction de teta, h et L.
5) Déterminer les bornes d'intégration teta l et teta 2 en fonction de h et L et montrer que Fy est donné par : k.q.(ro).L/h.racine(L/2)^2+h^2
Question complémentaire : Effectuer le même calcul pour Fx et montrer que Fx=O.
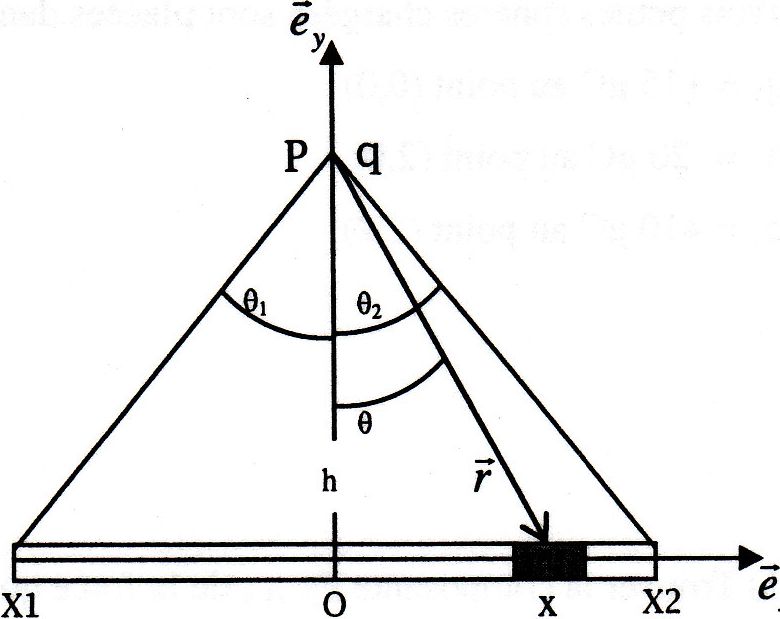
La Figure montre une tige fine, rectiligne, de longueur L et portant une densité de charge linéique p. Une charge q est placée au point P, sur la médiatrice de la tige à une distance h de son milieu O.
Chaque élément dx, placé à la distance r par rapport à P, porte une
charge (ro).dx et va exercer sur q une force proportionnelle à r/r^3*(q.(ro)).dx
La force totale devient : ftot=int( entre x1x2 )k.(q(ro).r)/r^3 dx
1) Donner sans la résoudre, l'expression de Fy la composante de FT,t suivant êy en fonction de r, teta et dx.
Pour résoudre cette équation un changement de variable(r;x)--teta est necessaire
2) Dans le triangle (0, P, x), exprimer r et x en fonction h et teta
3) A partir de l'expression de x, exprimer dx en fonction de h, teta et dû.
(Vous aurez besoin de la relation : d(tan(teta)) = 1/ cos^2 teta
4) Effectuer le changement de variable en remplaçant x, r et dx par leurs valeurs dans l'expression obtenue au 1) et en déduire Fy en fonction de teta, h et L.
5) Déterminer les bornes d'intégration teta l et teta 2 en fonction de h et L et montrer que Fy est donné par : k.q.(ro).L/h.racine(L/2)^2+h^2
Question complémentaire : Effectuer le même calcul pour Fx et montrer que Fx=O.
Personne pour m'aider ? bon tant pis je vais me débrouiller seul a bientot
1)
On projette chaque force élémentaire sur y en multipliant par cos donc :
donc :
2)
r = h / cos
x = h tan
3)
dx = h d(tan )
)
dx = (h / cos2 ) d
) d
4)
Quelque chose comme ça pour commencer...
je te remercie pour ces précisions et de t'y être intéressé je vais maintenant continuer seul
a bientôt.
Bonjour,
Je me pose une question par rapport à ce problème. Si je décompose le vecteur r j'obtient r = r sin ey - r cos
ey - r cos ey ce qui me donne
ey ce qui me donne x2x2 (-kq ro/ h) cos
x2x2 (-kq ro/ h) cos d
d . Je me retrouve donc avec un - qui dérange. Je ne sais pas ou je me suis trompée. Quelqu'un peut m'aider ?
. Je me retrouve donc avec un - qui dérange. Je ne sais pas ou je me suis trompée. Quelqu'un peut m'aider ?


