Inscription / Connexion Nouveau Sujet
exercice dynamique du point
Bonjour, je n'arrives pas à faire cet exercice:
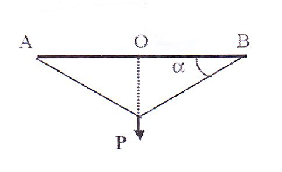
Un brin de caoutchouc de longueur 2L non tendu est fixé entre deux points A et B. On admettra que son poids est n'égligeable et que le brin est horizontal. On
accroche un poids P au milieu O de AB. Sachant que le caoutchouc tendu avec une force F s'allonge de l tel que F = kl, exprimer P en fonction de k, L et alpha.
J'ai commencé à faire le bilan des forces: P+F=0
et P=-F et F=kl et F=P*tan(alpha), Ob=L et PB= L+l
Merci pour votre aide
Bonjour goody,
Attention a la relation de l'enonce F = kl : l represente l'allongement du ressort par rapport a sa longueur L lorsqu'il n'est pas tendu. Si on appelle M la position du point d'attache du poids, on a l = AM - AO, avec AO = L et AM = 
(AO2 + OM2). Dans cette relation OM = L.tan
bien sur. Tu peux donc maintenant exprimer F en fonctino des variables L et du probleme.
Maintenant les deux forces F qui apparaissent sont portees respectivement par MA et MB. C'est leur composante verticale qui va equilibrer le poids. Il faut donc projeter F sur MO ce qui donne Fv = F.cos(
/2-) = F.sin (Fv pour "composante verticale de F").
La condition d'equilibre est donc mg = 2Fv.
Tu as tous les elements en main pour terminer toi-meme ton exercice.
A bientot, Prbebo.
Je viens de m'apercevoir qu'il est inutile de passer par Pythagore pour calculer AM... on a simplement AM = AO/cos = L/cos.
L'allongement d'un ressort est donc l = AM - AO = L(1/cos - 1). La force F d eveloppee par chaque ressort est F = kl = kL(1/cos - 1).
La projection de la force F sur la verticale est Fv = F.sin = kL(tan - sin).
Et la condition d'equilibre est mg = 2.Fv.
A bientot, prbebo.
Annuler
connectez vous