Inscription / Connexion Nouveau Sujet
Exercice du remonte pente
Bonjour, j'aimerais faire cet exercice donné dans un sujet d'examen de mon université. Pouvez-vous m'aider ?
Un skieur de masse m (avec son équipement), est tiré par la perche d'un téléski ; celle-ci fait un angle 
avec la piste. La piste est un plan incliné formant un angle 
avec le plan horizontal. Le skieur est en mouvement de translation rectiligne et uniforme. Les forces de frottement sont équivalentes à une force (de norme f). parallèle à la piste.
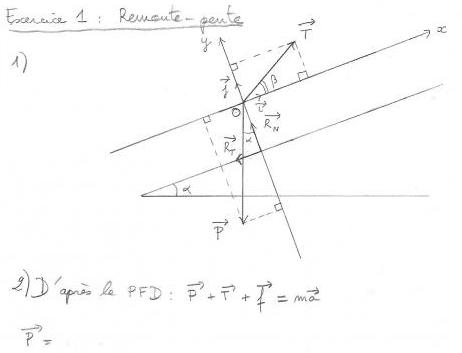
| 1. | Faites un schéma propre de la situation. Vous ferez figurer les forces exercées sur le skieur de manière à ce que celles-ci soient conformes (en norme, en sens et en direction) à la situation décrite. |
| 2. | Choisissez un système d'axes qui vous paraît commode pour résoudre le problème puis donner l'expression des composantes selon ces axes de la force de tension , et f. |
| 3. | Calculez la valeur de la norme de |
| 4. | Trouvez l'expression littérale du coefficient de frottement dynamique |
| 5. | Calculez la valeur numérique de |
Données : g
10 m.s-2 ; m=80 kg ; cos 0,9 ; sin 0,4 ; cos 0,8 ; sin 0,6 ; f=100 N.Bonjour
Commence par faire un schéma soigné où tous les vecteurs forces sont représentés.
Ecrit l'expression vectorielle de la relation fondamentale de la dynamique ; projette cette relation sur les deux axes et tu pourras répondre aux différentes questions.
Si tu veux, tu peux scanner ton schéma et le poster ici.
Tu oublies l'action de la neige sur les skis qui peut être considérée comme la somme de deux forces :
Une force normale perpendiculaire à la piste
Une force colinéaire à la piste constituant la force de frottement f.
Tu es ici dans le cas simple d'une accélération nulle.
Revois ton cours sur la définition du coefficient de frottement.
Tu oublies l'action de la neige sur les skis qui peut être considérée comme la somme de deux forces :
Une force normale perpendiculaire à la piste
Une force colinéaire à la piste constituant la force de frottement f.
Tu es ici dans le cas simple d'une accélération nulle.
Revois ton cours sur la définition du coefficient de frottement.
Mais ils disent dans l'énoncé que les forces de frottement sont équivalentes à une force \vec{f} (de norme f) parallèle à la piste. Est-ce que ça veut dire qu'on doit négliger
D'accord avec ce que tu as écrit dans ton message du 28-10-18 à 23:03 mais tu oublies la réaction normale de la piste :
La force de frottement ici est la réaction tangentielle de la piste souvent notée .
Or, tu as étudié en cours la relation entre RN, RT et le coefficient de frottement dynamique noté ici µd.
Puisque l'accélération par rapport à la piste est nulle, la somme des différents vecteurs forces est le vecteur nul. Projette cela sur les deux axes et tu vas obtenir un système de deux équations à deux inconnues : T et µd.
Tu as juste commis une erreur de projection concernant le poids :
Désolé : j'aurai dû le signaler dès ton message du 28-10-18 à 23:03 .
Annuler
connectez vous