Bonsoir
Pistes de réflexions possibles :
A très basse fréquence, l'impédance d'un condensateur tend vers l'infini. Dans ces conditions chaque association (R//C) est équivalente à R seule. A très basse fréquence, tout se passe comme si les deux condensateurs n'existaient pas.
Tu peux ensuite montrer qu'à très haute fréquence, chaque association (R//C) se comporte comme un condensateur seul. A très haute fréquence, le filtre se comporte comme si les deux résistances étaient enlevées.
A très basse fréquence : G=-20dB : cela permet d'obtenir R2 connaissant R1.
A très haute fréquence, G=-40dB : cela permet d'obtenir C2 connaissant C1.
PS : tu connais sûrement la notion de diviseur de tension...

Bonjour,

Attention au choix du titre, à minima préciser le chapitre abordé parce que "exercice difficile" ne donne aucune idée du thème en question ...

Bonjour, merci pour votre aide.
J'ai utilisé un diviseur de tension mais ce que je trouve que parait très faible:

R2=21

alors que R1=90k

Pardon, c'est bon j'ai juste fait une erreur sur ma calculatrice

Tu n'y es pas vraiment...J'espère que la notion de diviseur de tension ne te pose pas de problème...  A très basse fréquence, le module H de la fonction de transfert vérifie :



Or, comme déjà expliqué, à très basse fréquence :



Je te laisse déterminer R2...

A très haute fréquence :



Or, comme déjà expliqué, à très haute fréquence :



Je te laisse continuer... Je ne suis pas sûr que la question 3), telle que tu l'as recopié ici soit complète...

J'avais réussi la question 1), j'avais seulement fait une erreur en remplaçant par la valeur de chaque composé. J'ai réussi à faire la question 2 également.
Pour la 3) par contre j'ai un problème:
Je voulais utiliser le fait que G(w)=/H(w)/=/(us/ue)/
Et remplacer ue pas sa valeur et G(w) par la sienne mais ça ne mène nul part

Tu es pourtant sur la bonne piste mais il faut réfléchir en tenant compte du diagramme de Bode. Pour toute fréquence égale ou supérieure à 10kHz, H=0,01 et le filtre n'introduit aucun déphasage. Chaque composante du signal (fondamental et harmoniques) voit donc son amplitude divisée par 100 sans création de déphasage...
Peux-tu vérifier ta copie de la question 4 : le "27" ne devrait-il pas être remplacé par un "2" ?

Pour la question 4, c'est bien un 2 et non un 27, j'ai mal recopié.
Pour la question 3, je ne vois pas comment utiliser les amplitudes et le fait que ces dernières soient divisées

Pour 3 : quelle est l'expression précise de u_e(t) ?
Il suffit alors de diviser par 100 l'amplitude de chaque composante sinusoïdale.
Je te joins le diagramme de Bode précis du filtre. Cela pourra peut-être t'aider...

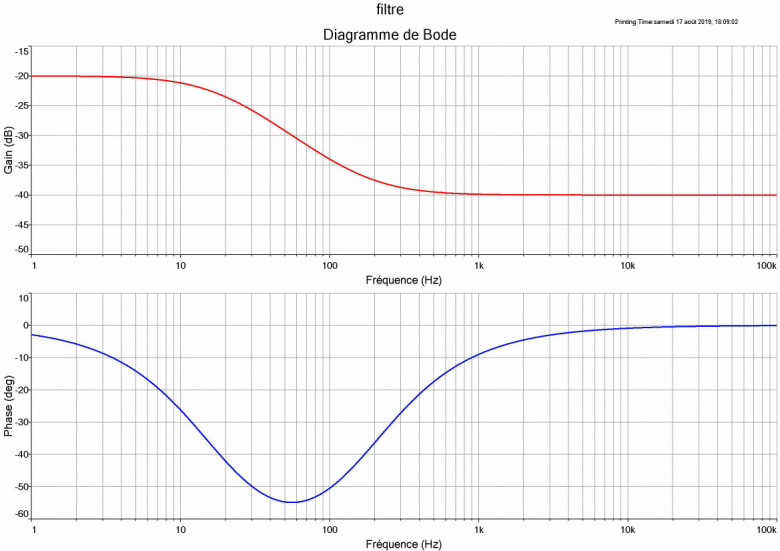
Pour la question 3, on n'a pas plus d'information que ce que j'ai marqué dans l'énoncé soit:
"ue(t) un signal périodique de 10 kHz avec seulement les deux premières harmoniques paires d'amplitudes respectives 6 V et 4 V."

Le plus souvent, on fait la différence entre le signal fondamental sinusoïdal de fréquence f et les signaux sinusoïdaux harmoniques de fréquences 2f, 3f, 4f... Parfois, on nomme signaux harmoniques tous les signaux sinusoïdaux. Comment fait ton professeur ? Peut-être faut-il comprendre :

  

avec f=10kHz ???  On obtient dans ce cas très simplement, comme déjà écrit :



les tensions instantanées étant exprimées en volts. Attention, tel qu'est posé l'énoncé, je ne suis pas du tout certain de l'expression de u_e(t) mais j'espère que tu as compris le principe !

Je crois que j'ai compris, je vais essayé de l'appliquer à la question 4.
Comme c'est une professeur que je n'ai jamais eu, je ne sais pas comment sont ses notations.
Merci beaucoup en tout cas.