Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieurForum supérieur ingé PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau école ingénieur
Partager :

exercice de thermodynamique dans le cas d'un cylindre

Posté par
vovik 25-03-18 à 22:28

Bonjour,
je fait appel à votre aide car je tourne en rond depuis 2 jours sur ce exercice:

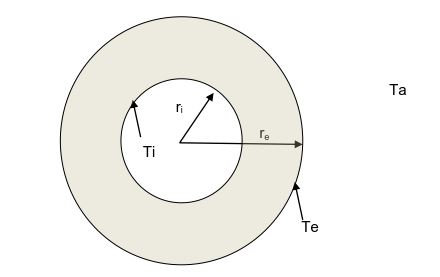
On souhaite étudier la diffusion de la chaleur dans un dispositif cylindrique creux constitué d'un matériau
inerte ayant une conductivité \lambda (fig. ci-dessous).

On suppose qu'il existe un transfert de chaleur par convection ( entre la surface externe du cylindre (T_{e}) et le milieu environnant (T_{a})) caractérisé par le coefficient h.

1. Etablir l'équation différentielle du transfert de chaleur à la surface du cylindre.

2. Déterminer T(r). Vérifier qu'on retrouve le résultat de la question A.3 lorsque la condition h>> \lambda est vérifiée. Quelle interprétation peut-on en faire ?
voici la question A.3  En utilisant les données de la figure, établir l'expression de T(r).

voici le résultat que j'ai trouvé à la question A.3:
T(r)=T_i+(T_e-T_i)\frac{ln(\frac{r}{r_i})}{ln(\frac{r_e}{r_i})}


3. Calculer le flux passant à travers un cylindre de rayon  r et de longueur l ; en déduire l'expression
de sa résistance thermique.

Voici mon raisonnement:

1. Le transfert de chaleur à la surface du cylindre est régit par la Loi de Newton ou la densité de chaleur s'écrit:
\varphi_r|_{r=r_e}=h\times(T|_{r=surface}-T_{\infty })
soit dans ce cas:
\varphi_r|_{r=r_e}=h\times(T_{e}-T_{a })
\varphi_r|_{r=r_e}=h(T_{e}-T_{a }) <=> \varphi_r2 \pi r_e l=h(T_{e}-T_{a }) 2 \pi r_e l=>\phi=h(T_{e}-T_{a }) 2 \pi r_e l ou \phi est le flux de chaleur.

Déjà ici j'ai du mal car je ne trouve pas l'équation différentielle comme si je l'aurais fait à travers un bilan de chaleur en coordonnées cylindriques (unidimensionnel, régime permanent sans génération de chaleur) en utilisant la loi de Fourier   \varphi=-\lambda \vec{grad}(T)=-\lambda \frac{\partial T}{\partial r}
\frac{1}{r}\frac{\partial }{\partial r}[r \lambda \frac{\partial T}{\partial r}]=0.

Quelle est l'équation différentielle qu'on me demande ici?

2. Je pense que si je trouve l'équation différentielle de la question 1 je devrai trouver sans difficulté l'expression de T(r)

Pourriez - vous m'indiquer qu'est - ce que ne va pas dans mon raisonnement?

Je vous remercie par avance.

Posté par
vovikre : exercice de thermodynamique dans le cas d'un cylindre 25-03-18 à 22:32

Oups j'ai oublié l'image:

exercice de thermodynamique dans le cas d\'un cylindre

Merci d'avance.

Posté par
vanoisere : exercice de thermodynamique dans le cas d'un cylindre 25-03-18 à 23:31

Bonsoir
Ton énoncé me semble bien confus et parfois totalement aberrant : il n'est pas possible de raisonner sur l'inégalité h>> pour la bonne raison qu'il n'est pas possible de comparer deux grandeurs physiques de dimensions  différentes. C'est un peu comme si on te demandait de tirer des conséquence du fait qu'une longueur puisse être beaucoup plus grande qu'une durée !!!
Cela dit, j'imagine que l'on travaille en régime permanent, le transfert thermique étant radial. Dans ces conditions, le flux thermique \phi à travers un cylindre de rayon r compris entre ri et re est indépendant de r. Il se calcule en r=re en appliquant, comme tu l'as fait, la loi de Newton :
\phi=h(T_{e}-T_{a})2\pi r_{e}l
Dans le métal, ce flux thermique est le flux à travers le cylindre de rayon r du vecteur densité de flux thermique :
\overrightarrow{j_{Q}}=j_{Q}.\overrightarrow{u_{r}}\quad avec\quad\overrightarrow{j_{Q}}=-\overrightarrow{grad}\left(T\right)=-\lambda.\frac{dT}{dr}.\overrightarrow{u_{r}}

\phi=j_{Q}.2\pi.r.l=-2\pi.r.l.\lambda.\frac{dT}{dr}
Après simplification :

\frac{dT}{dr}=-\frac{h.r_{e}.\left(T_{e}-T_{a}\right)}{\lambda}\cdot\frac{1}{r}
Il s'agit sans doute de l'équation différentielle vérifiée par T(r) dont parle l'énoncé.
Je te laisse intégrer...
Pour obtenir la résistance thermique, tu peux écrire :

T_{i}-T_{a}=\left(T_{i}-T_{e}\right)+\left(T_{e}-T_{a}\right)=R_{th}.\phi
Je te laisse réfléchir à tout cela et j'espère terminer.

Posté par
vanoisere : exercice de thermodynamique dans le cas d'un cylindre 25-03-18 à 23:33

J'allais oublier : ton résultat "A3" me semble cohérent mais je n'ai pas l'énoncé intégral...

Posté par
vanoisere : exercice de thermodynamique dans le cas d'un cylindre 25-03-18 à 23:45

A la réflexion : à propos de la comparaison aberrante : h>> \lambda ; il s'agit sans doute de considérer la résistance thermique du cylindre très grande devant la résistance thermique de l'interface cylindre - air ...

Posté par
vovikre : exercice de thermodynamique dans le cas d'un cylindre 26-03-18 à 00:19

Bonsoir Vanoise je te remercie énormément pour ton  aide.

Voici l'intégralité de l'énoncé:
On souhaite étudier la diffusion de la chaleur dans un dispositif cylindrique creux constitué d'un matériau inerte ayant une conductivité \lambda

A. On considérera dans cette partie que les phénomènes radiatifs et convectifs sont négligeables.
  
1. Sachant que Te est supérieure à Ti, écrire l'équation de la diffusion de la chaleur en coordonnées cylindriques. (fig. ci-dessous).

  2. En déduire l'équation différentielle permettant de calculer la température en un point situé à une
distance r du centre (re>r>ri).

  3. En utilisant les données de la figure, établir l'expression de T(r).

  4. Déterminer le profil de température en traçant la courbe (T-Ti)/(Te-Ti) en fonction de r.

  5. Établir l'expression de la densité de flux circulant entre les deux faces du cylindre.

  6. Utiliser le résultat obtenu pour calculer le flux passant à travers un cylindre de rayon r et de longueur l ; en déduire l'expression de sa résistance thermique.

  7. On souhaite connaitre l'évolution de ces grandeurs lorsque la partie pleine du cylindre est très
fine ; établir la fonction T(r), le flux ainsi que la résistance thermique. Conclusion ?


B. On suppose maintenant qu'il existe un transfert de chaleur par convection ( entre la surface externe du
cylindre (Te) et le milieu environnant (Ta)) caractérisé par le coefficient h.

  1. Établir l'équation différentielle du transfert de chaleur à la surface du cylindre.

  2. Déterminer T(r). Vérifier qu'on retrouve le résultat de la question A.3 lorsque la condition h>> \lambda est vérifiée. Quelle interprétation peut-on en faire ?

  3. Calculer le flux passant à travers un cylindre de rayon r et de longueur l ; en déduire l'expression de sa résistance thermique.

La partie A du problème je l'ai traité déjà.

Cette équation différentielle:
\frac{\partial T}{\partial r}=-\frac{h\times r_e\times(T_e-T_a)}{\lambda}\times \frac{1}{r}
est valable uniquement pourr\geq r_e ?
Car si r est plus petite que re on est dans le corps du cylindre ou c'est le phénomène de la conduction et donc l'équation est différente.
Je dis ça car si j'intègre sur r_i jusqu'à r_e je ne peux pas utiliser cette relation.

Cordialement.

Posté par
vovikre : exercice de thermodynamique dans le cas d'un cylindre 26-03-18 à 08:49

Vanoise bonjour,

Pour le question B 2 :
Déterminer T(r). Vérifier qu'on retrouve le résultat de la question A.3 lorsque la condition h>> \lambda est vérifiée. Quelle interprétation peut-on en faire ?

je ne suis pas sur du résultat, car voici ce que je trouve:

\frac{\partial T}{\partial r}=-\frac{h }{ \lambda}r_e (T_e-T_a)\frac{1}{r}=>\int \partial T=-\frac{h }{ \lambda}r_e (T_e-T_a)\int\frac{1}{r} \partial r=> T(r)=-\frac{h }{ \lambda}r_e (T_e-T_a)ln(r)+C
en utilisant la condition limite je trouve la constane C:
T(r=r_e)=T_e=-\frac{h }{ \lambda}r_e (T_e-T_a)ln(r_e)+C=>C=T_e+\frac{h }{ \lambda}r_e (T_e-T_a)ln(r_e)
ainsi la fonction T(r) s'écrit:
T(r)=-\frac{h }{ \lambda}r_e (T_e-T_a)ln(r)+T_e+\frac{h }{ \lambda}r_e (T_e-T_a)ln(r_e)
soit
T(r)=\frac{h }{ \lambda}r_e (T_e-T_a)(ln(r_e)-ln(r))+T_e
au final:
T(r)=\frac{h }{ \lambda}r_e (T_e-T_a)ln(\frac{r_e}{r})+T_e.

Avec la condition : h>> \lambda=> \frac{h}{\lambda}>>1

Sa m' amène à rien. Et donc sa me met en doute concernant l'équation différentielle trouvé à la question 1.

S'il te plaît pourrais-tu me montrer la solution ou me dire où j'ai faux?

Merci par avance.

  


  

Posté par
vanoisere : exercice de thermodynamique dans le cas d'un cylindre 26-03-18 à 17:13

Merci pour l'énoncé complet. Il confirme ma première impression. Il est vraiment mal conçu !

B1 : la loi de Newton n'est pas une équation différentielle. Je ne vois pourtant pas quoi répondre à part ce qui a déjà été fait :

\phi=h(T_{e}-T_{a})2\pi r_{e}l
Le sens positif du transfert est le sens du vecteur \overrightarrow{u_{r}} . Puisque ici : Ta>Te, \phi<0.

B2 : OK pour ta résolution de l'équation différentielle mais attention : elle utilise les lois de la conduction. Elle est donc valide uniquement pour ri<r<re. Énoncé mal conçu : on ne sait pas exactement quelles sont les températures connues (Te sûrement mais l'autre ?) et les températures inconnues. Je vais essayer de faire apparaître l'expression que tu as fournie en A3. L'intégration de l'équation différentielle conduit à :

T(r)=-\frac{h}{\lambda}r_{e}(T_{e}-T_{a})ln(r)+K
(K : constante d'intégration)
Cas particuliers :

T_{e}=-\frac{h}{\lambda}r_{e}(T_{e}-T_{a})ln(r_{e})+K

T_{i}=-\frac{h}{\lambda}r_{e}(T_{e}-T_{a})ln(r_{i})+K
Soustraction membre à membre :

T_{e}-T_{i}=\frac{h.r_{e}}{\lambda}\left(T_{e}-T_{a}\right)\ln\left(\frac{r_{i}}{r_{e}}\right)

T_{(r)}-T_{i}=\frac{h.r_{e}}{\lambda}\left(T_{e}-T_{a}\right)\ln\left(\frac{r_{i}}{r}\right)=\left(T_{e}-T_{i}\right)\frac{\ln\left(\frac{r_{i}}{r}\right)}{\ln\left(\frac{r_{i}}{r_{e}}\right)}=\left(T_{e}-T_{i}\right)\frac{\ln\left(\frac{r}{r_{i}}\right)}{\ln\left(\frac{r_{e}}{r_{i}}\right)}

Exactement la relation que tu as obtenue en A3 et cela sans faire d'approximation particulière ! normal : puisque l'étude se fait en étudiant uniquement le phénomène de conduction dans le métal dans les deux cas !

Je me permets d'insister : il est inconcevable de vouloir comparer h à {\normalcolor :\blue \lambda} dans la mesure où il s'agit de deux grandeurs de natures différentes (regarde les unités au besoin).
Réflexion faite, je pense que le concepteur de l'énoncé, s'attend à ce que les étudiants posent, dans la mesure où le phénomène de convection est négligé : Te=Ta dans toute la partie A.

Tu peux démontrer que négliger la convection est équivalent à poser Te=Ta en introduisant la notion de résistance thermique. Tu devrais arriver à la conclusion :

T_{e}\approx T_{a}\quad si\quad h.r_{e}\gg\lambda

Je te laisse réfléchir à cela et continuer. Mon message précédent fournit quelques indications sur la résistance thermique.

Posté par
vovikre : exercice de thermodynamique dans le cas d'un cylindre 26-03-18 à 18:33

Bonjour Vanoise,

merci infiniment,

pour la résistance thermique j'ai procédé ainsi:

flux du à la convection : \phi=2\pi r_elh(T_e-T_a)

flux du à la conduction :\phi=\frac{2\pi l\lambda}{ln(\frac{r_e}{r_i})} (T_i-T_e)

\phi \times \frac{1}{2\pi r_elh}=(T_e-T_a)

\phi\times \frac{ln(\frac{r_e}{r_i})}{2\pi l\lambda}=(T_i-T_e)

(T_i-T_e)+(T_e-T_a)=\phi \times \frac{1}{2\pi r_elh}+ \phi\times\frac{ln(\frac{r_e}{r_i})}{2\pi l\lambda}=\phi (\frac{1}{2\pi r_elh}+\frac{ln(\frac{r_e}{r_i})}{2\pi l\lambda})

(T_i-T_a)=\phi (\frac{1}{2\pi r_elh}+\frac{ln(\frac{r_e}{r_i})}{2\pi l\lambda})

comme : \Delta T=\phi\times R_{th}

alors : R_{th}=\frac{1}{2\pi r_elh}+\frac{ln(\frac{r_e}{r_i})}{2\pi l\lambda}

Si de plus on considère que le cylindre creux est d'une épaisseur très fine tels que  
e=(r_e-r_i)<<r_i

alors:   ln\frac{r_e}{r_i}\approx\frac{e}{r_i}

ainsi: \frac{ln(\frac{r_e}{r_i})}{2\pi l\lambda}=\frac{e}{2\pi r_i l\lambda}

et donc : R_{th}=\frac{1}{2\pi r_elh}+\frac{e}{2\pi r_i l\lambda}

comme (r_e \approx r_i)=r

alors: R_{th}=\frac{1}{2\pi rlh}+\frac{e}{2\pi r l\lambda}

R_{th}=\frac{1}{S_{cylindre}h}+\frac{e}{S_{cylindre}\lambda}


Cordialement.

Posté par
vanoisere : exercice de thermodynamique dans le cas d'un cylindre 26-03-18 à 18:56

Tout cela est excellent !
Tu vas finir par croire que je fais une fixation sur cette histoire de comparaison de h à mais il s'agit d'un point fondamental utile dans tous les domaines. Je pars de tes deux expressions des écarts de températures puis j'effectue une division « membre à membre » :

\phi\times\frac{1}{2\pi r_{e}lh}=(T_{e}-T_{a})

\phi\times\frac{ln(\frac{r_{e}}{r_{i}})}{2\pi l\lambda}=(T_{i}-T_{e})

\frac{T_{a}-T_{e}}{T_{e}-T_{i}}=\frac{\lambda}{h.r_{e}.\ln\left(\frac{r_{e}}{r_{i}}\right)}

Suppose maintenant : h.r_{e}\gg\lambda ; tu as nécessairement :

T_{a}-T_{e}\ll T_{e}-T_{i}

L'écart de température entre l'air ambiant et la paroi est négligeable devant la variation de température provoquée par le phénomène de conduction à travers le métal. On peut négliger le phénomène de convection devant le phénomène de conduction. Cela est cohérent avec le fait que la résistance thermique due au phénomène de convection \left(\frac{1}{2\pi r_{e}.l.h}\right) est négligeable, dans ce genre de situation,  devant la résistance thermique due à la conduction \left(\frac{ln(\frac{r_{e}}{r_{i}})}{2\pi.l.\lambda}\right) .

Posté par
JulesMhzre : exercice de thermodynamique dans le cas d'un cylindre 01-04-20 à 10:09

Bonjour,

Je me permets de remonter un peu ce sujet car j'ai quelques soucis aussi.

Dans la partie A, " les phénomènes radiatifs et convectifs sont négligeables", à la question 1, l'équation de la diffusion de la chaleur en coordonnées cylindriques est bien :
(1/r)*d/dr*(r*dT/dr)=0 ?
à la question 2, puisque l'énoncé n'a pas encore parlé de la température du milieu environnant (Ta), comment est-ce que je j'exprime l'équation différentielle ?

Merci !

Posté par
vanoisere : exercice de thermodynamique dans le cas d'un cylindre 01-04-20 à 12:10

Bonjour
Dans la partie A, négliger les phénomènes autres que la conduction revient à considérer Te=Ta. L'équation générale de conservation de l'énergie thermique dans un solide conduit, en régime permanent, à considérer le laplacien de T nul en tout point. Cela donne, en coordonnées cylindro-polaire et en tenant compte des invariances, ce que tu as écrit.  Il s'agit d'une équation différentielle du second ordre pas évidente à intégrer. Il est donc préférable, comme cela a été fait précédemment, de considérer le flux thermique \phi indépendant de r en regime permanent, d'exprimer \phi en fonction de r et de jQ (densité de flux thermique) puis d'exprimer jQ en tenant compte de la loi de Fourier.

Posté par
JulesMhzre : exercice de thermodynamique dans le cas d'un cylindre 01-04-20 à 22:03

Bonjour Vanoise,

Merci pour ta réponse.

Donc si je comprends bien j'ai :

flux=h.(Ti-Te).2.Pi.re.l

Et jq=-grad(T)=-lambda.dT/dr.ur

Donc flux=jq.2*Pi*r*l = -2.Pi.r.l.lambda.dT/dr

Finalement dT/dr = -h.re.(Ti-Te)/(lambda.r)

C'est bien quelque chose comme ça ?

Merci !

Posté par
vanoisere : exercice de thermodynamique dans le cas d'un cylindre 02-04-20 à 11:47

Bonjour

Ce que tu as fait est correct mais tient compte de la convection puisque tu fais intervenir la constante h. Cela correspond au résultat du message du 25-03-18 à 23:31. Négliger la convection revient à poser Te=Ta et à n'étudier que la conduction dans le solide. Le flux thermique est indépendant de r et donc considéré comme fixe en régime permanent :

\phi=2\pi.r.l.j_{Q}=-2\pi.r.l.\lambda\cdot\frac{dT}{dr}

Séparation des variables :

dT=-\frac{\phi}{2\pi.l.\lambda}\cdot\frac{dr}{r}

Intégration :

T_{\left(r\right)}=-\frac{\phi}{2\pi.l.\lambda}\cdot\ln\left(r\right)+K
(K : constante d'intégration)

T_{e}=T_{a}=-\frac{\phi}{2\pi.l.\lambda}\cdot\ln\left(r_{e}\right)+K

T_{i}=-\frac{\phi}{2\pi.l.\lambda}\cdot\ln\left(r_{i}\right)+K

Par soustractions membre à membre, on obtient le résultat fourni par vovik dans son premier message :

T_{(r)}=T_{i}+(T_{e}-T_{i})\cdot\dfrac{\ln\left(\frac{r}{r_{i}}\right)}{\ln\left(\frac{r_{e}}{r_{i}}\right)}


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !