Inscription / Connexion Nouveau Sujet
Exercice de Physique
Bonjour à tous, j'ai une question d'un exercice de Physique sur laquelle je bloque totalement (par manque d'exemple dans le cours ...). Voici le sujet :
Une motrice de train est alimentée en courant continu.
L'alimentation est réalisée par des sous stations Si distantes de D. Ces stations relient les rails (portées au potentiel nul VT=0 ) a la caténaire AB. Chaque source Si sera représentée par un générateur idéal de tension E.
La motrice M est branchée entre les rails et la caténaire. On supposera que son moteur est alimenté par un courant constant n (eta), c'est à dire qu'il pourra être modélisé par un générateur de courant idéal.
De plus, la caténaire présente une résistance électrique proportionnelle à sa longueur : si elle mesure l, sa résistanceest pl, p est la résistance linéique.
La résistance électrique des rails est négligée.
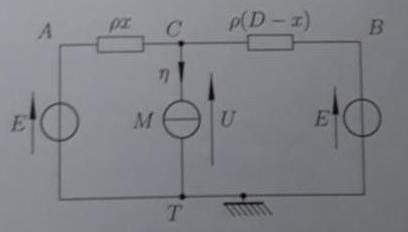
1. On considère une section de ligne de longueur D alimentée par deux stations. On note x la longueur de caténaire séparant la motrice de la sous tension S1.
A. En utilisant la loi des noeuds en terme de potentiel, exprimer la tension U = Uct aux bornes de la motrice et en déduire la chute de tension deltaU=E-U en fonction de x, p et D
J'ai tenté de déterminer le potentiel en C et en T mais en vain je crois.
Voici la photo du schéma associée
Si une âme charitable veut bien m'aider, je l'en remercie d'avance
Bonjour
En écrivant que la tension U recherchée est à la fois :
U = UCA + UAT
et
U = UCB + UBT
et en tenant compte de la loi des nœuds telle que résumée sur le schéma, tu devrais t'en sortir...
Je vous remercie pour votre réponse et votre rapidité.
Dois je utilisé la loi d'Ohm ? Ou dire que UCT = (VT-VC+E)/R ?
Je suis un petit peu perdu !
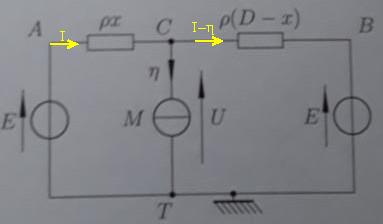
En passant par le point A :
U=E -  .x.I
.x.I
En passant par le point B :
U=E- .(D-x).(I-
.(D-x).(I- )
)
Tu élimine "I" entre ces deux équations pour obtenir le résultat.
L'intensité entre le point C et la résistance, ça ne serait pas plutôt n-i orientée de la résistance à C donc juste un changement de signe (du au changement de sens )? Et du coup ça serait bon par rapport à l'orientation de l'intensité ?
Ça serait par conséquent, U=E-p(D-x)(n-I) ?
Et concernant votre réponse, je ne vois pas comment on peut retirer les I .
La première égalité permet d'écrire :
En remplaçant dans la deuxième équation "I" par l'expression ci-dessus, tu obtiens le résultat demandé.
Ah d'accord, oui, c'est simple, j'avais mal compris la question ! Merci beaucoup de m'avoir consacrer du temps !😊