Niveau licence

Exercice de mécanique : mouvement circulaire

Posté par
thais13 11-11-17 à 21:52

Bonjour ! Je n'arrive pas à comprendre un exercice de mécanique dont voici le sujet :

On lance une luge dans une piste qui lui impose une trajectoire composée de deux demi-cercles successifs (donc en forme de ”S”). Le premier tronçon à un rayon de 5,00 m, le second de 10,0 m. La vitesse initiale est de 6,00 m s −1 .

1. On néglige les frottements, ce qui implique que le mouvement est uniforme. Calculer les vecteurs accélération et vitesse dans les 2 parties de la trajectoire.

2. On suppose maintenant un frottement faible mais constant qui ajoute une composante au vecteur accélération tangente à la trajectoire dans le sens opposé au mouvement, d'intensité 1,00 · 10 −3 m s −2 . Calculer les vecteurs accélération et vitesse dans les 2 parties de la trajectoire. Quelle est la vitesse à la sortie de la piste ?

Je ne parviens pas trop à démarrer... Est-ce que la vitesse angulaire est égale à la norme du vecteur vitesse pour chacune des parties de la trajectoire ? Dans mon cours, il est écrit que : vitesse angulaire = v0/r dans ce cas précis mais je ne comprend pas pourquoi...

Merci d'avance.

Posté par re : Exercice de mécanique : mouvement circulaire 11-11-17 à 22:14

Bonsoir
Dans le cas d'un mouvement circulaire uniforme, l'accélération est normale centripète de norme (v²/R). Cela doit te permettre de démarrer. Si le mouvement n'est plus uniforme, il faut ajouter à l'accélération une composante tangentielle (-dv/dt). Revois bien ton cours sur le sujet.

Posté par re : Exercice de mécanique : mouvement circulaire 11-11-17 à 22:54

1. Pour la première phase :
phi(point) = v0/R1
Mais est-ce que cela revient à la même chose de dire : v(vecteur) = (v0/R1).e phi (vecteur unitaire tangentiel) ?
Je vois que la formule générale est : v(vecteur) = R1.phi(point).e phi (vecteur) donc je ne sais pas laquelle est à utiliser pour cet exercice.
Ensuite, on peut dire que : a(vecteur) = -((v0)²/R1).e r (vecteur unitaire dirigé vers le centre du cercle).

Pour la deuxième phase : comme la vitesse initiale a un sens opposé à v0, on ajoute un signe "-" devant l'expression de la vitesse :
phi(point) = -v0/R2
a(vecteur) = -((v0)²/R2).e r (vecteur)

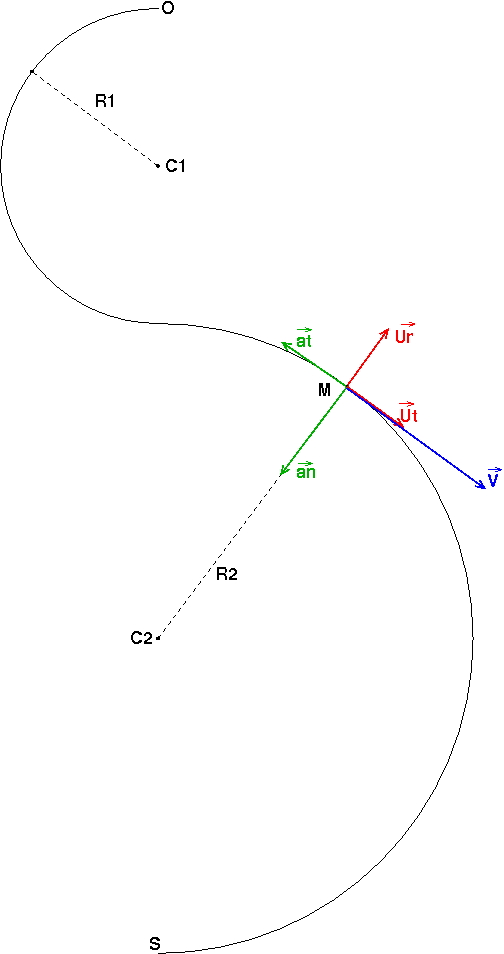
Posté par re : Exercice de mécanique : mouvement circulaire 12-11-17 à 11:26

Pour la partie 2 : tu n'y es pas vraiment... J'espère que le schéma ci-dessous t'aidera à comprendre. Dans le cas le plus général, l'accélération, mesurée dans un repère lié à la piste, peut s'écrire comme une somme de deux vecteurs :
1° : l'accélération normale centripète :

$\overrightarrow{a_{n}}=-\frac{v^{2}}{R}\cdot\overrightarrow{u_{r}}$
avec R = R₁ ou R=R₂ suivant la portion de piste. La norme v du vecteur vitesse est constante à la question 1) mais diminue au cours du temps à la question 2).
2° : l'accélération tangentielle :

$\overrightarrow{a_{t}}=\frac{dv}{dt}\cdot\overrightarrow{u_{t}}$
Selon l'énoncé, le vecteur a_t est de sens opposé au vecteur u_t et de norme 1,00.10^-3m/s². Par identification on obtient :

$\frac{dv}{dt}=-1,00.10^{-3}m/s^{2}$

Par intégration, sachant que la vitesse initiale vaut 6,00m/s, on obtient l'expression de v en fonction du temps, en prenant l'origine des dates confondue avec l'instant de départ en O :

$v=-10^{-3}\cdot t+6\quad\text{(en m/s)}$

La distance réellement parcourue le long de la piste entre la position de départ O et un point quelconque M (position à la date t) est notée s (abscisse curviligne) ; elle vérifie :

$v=\frac{ds}{dt}$

Par intégration :

$s=-5.10^{-4}\cdot t^{2}+6\cdot t$

Tu remarquera une certaine analogie avec l'étude du mouvement rectiligne uniformément retardé. Sachant qu'en sortie de piste (M au point S) :

$s_{(S)}=\pi\cdot\left(R_{1}+R_{2}\right)$

... Je te laisse réfléchir à tout cela et, j'espère, terminer.

Exercice de mécanique : mouvement circulaire

Posté par re : Exercice de mécanique : mouvement circulaire 12-11-17 à 14:28

Je vous remercie pour votre réponse aussi détaillée cela m'a beaucoup aidé à comprendre !

Juste une toute petite question : pour la première question, puis-je écrire que vecteur v(t) = v0 . ut puisque la norme est constante ?

Pour la deuxième question vos explications sont très claires j'ai tout compris. Du coup j'imagine que pour répondre à la question il faut faire :
(R1+R2)pi = -5.10^-4 tS^2 + 6tS
-5.10^-4 tS^2 + 6tS + 15pi = 0
On calcule delta et on trouve deux valeurs de tS : 11992 secondes ou 8,3 secondes.
Cela nous donne deux valeurs de v :
+ ou - 5,99 m. s^-1
Comme nous voulons une vitesse positive (je ne sais pas trop expliquer pourquoi), v = 5,99 m. s^-1

Posté par re : Exercice de mécanique : mouvement circulaire 12-11-17 à 15:05

OK pour 1
Pour 2) : c'est vrai que l'équation admet deux solutions réelles :
t1=7,86s et t2=11,2.10³s
Deux méthodes possibles pour trouver celle qui est physiquement réaliste :
1° : Puisque le vecteur vitesse reste constamment orienté dans le sens du vecteur u_t (pas d'inversion du sens du mouvement), il faut nécessairement obtenir en S une vitesse positive. Cela impose :

$t_{S}<\frac{6}{10^{-3}}=6.10^{3}s$
Cela exclue la solution t2 ; donc t_S=t₁=7,86s

2° : tu peux aussi calculer la durée du parcours dans le cas de la question 1) où la vitesse reste constante et égale à 6m/s :

$\varDelta t=\frac{s_{S}}{v_{0}}=\frac{\pi\cdot\left(R_{1}+R_{2}\right)}{v_{0}}=\frac{15\pi}{6}\approx7,85s$

Les frottements étant ici très faible, la valeur de la durée à retenir est de peu supérieure à $\varDelta t$ mais sûrement pas 1526 fois plus grande !

La vitesse de sortie est ainsi :

$v_{s}=-10^{-3}\cdot t_{1}+6\approx5,99m/s$

Remarque : je trouve l'influence des frottement particulièrement faible.. Es-tu bien sûr de la valeur de l'accélération tangentielle : 1,00.10^-3m/s² ?