Inscription / Connexion Nouveau Sujet
Exercice de Mécanique des structure(RDM)
Bonjour à tous!
je sollicite votre aide pour mon exercice ci-après:Merci d'avance et que Dieu vous bénisse!
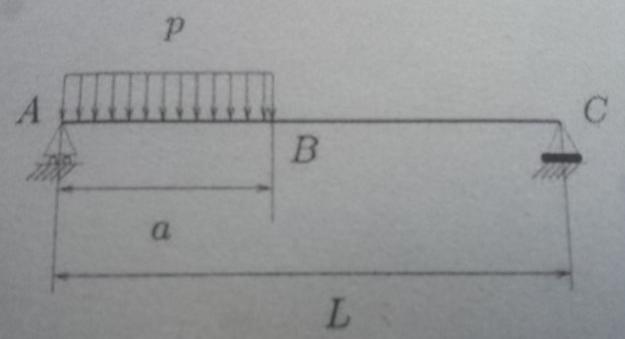
La poutre ci-dessous repose sur deux appuis simple et fixe et est soumise à une densité
linéaire de force verticale, constante et égale à p = 1,5 tonne/m sur [AB] et nulle sur [BC].
1. Calculer les réactions d'appui en A et C.
2. Calculer la distribution du moment fléchissant M(x) dans la poutre.
3. Trouver la valeur maximale du moment fléchissant M(x)
a) Calculer la valeur maximale de M(x) sur [AB]
b) Calculer la valeur maximale de M(x) sur [BC]
c) Conclure
Application numérique L=3cm et a=1cm
Bonjour a tous et mes respects a vous!
sincèrement dans la mesure du possible, aidez moi car j'en ai besoin pour comprendre mon exercice.
Concernant la question 1) en revisant mon cours je pense proceder a une decomposition des forces de reaction en A et en B. En effet on a par exemple en A, 2 forces hortogonales qui y sont appliquées.
Merci de m'eclaircir.
Bonjour,
Je suppose que les longueurs sont en m et non en cm.
La première question est un exercice de statique.
On remplace la charge uniformément répartie par une force localisée de valeur pa appliquée au milieu de AB.
Il faut utiliser les conditions d'équilibre de la poutre AC soumise aux forces RA, pa et RC.
J'ai trouvé RA= 12500 N et RC = 2500 N.
A vous lire. JED.
Bonjour!
vraiment merci pour votre reponse.
je n'ai pas bien compris votre demarche pour Ra et Rc.
en appliquant l'equation de moment en A, je trouve Rc=ap/L = 500N et Rc=p(1-a/L)+p.
Merci de me detailler avec les formules litterales votre demarche.
Bonsoir,
Si vous prenez l'équation des moments par rapport à A vous écrirez :
RC *L -pa*a/2= 0 ............
Sur le plan numérique : p=15000 N/m et pa= 15000 N
Continuez. JED.
Merci encore de votre reponse.
effectivement ça donne.
voici ce que j'ai fait:
Res/y: Ra+Rc-p=0 en appliquant l'equation des moments en A selon z: -a.p.a/2 + LRc=0 d'où Rc=a.a.p/2L = 2500N.
dans l'equation de moment on a: Ra= 12500N.
grace a vous tout est claire pour la première question.
pour la question 2) dois je decouper la poutre en differents ensembles?
> x appartenant a [A;B]
» x appartenant a [ B;C]
pour le premier intervalle, en regardant les actions a droite on a: Mzf= Rc.(L-x)
Mais j'en suis pas persuadé.
votre avis svp
Bonsoir,
Prenons le cas de A en B.
Soit S , située à x de A ,une section dans la poutre.
Les forces à gauche sont RA = 12500 N et une charge localisée p*x située à x/2 de S.
Donc Mf = 12500*x -7500*x^2
Le signe deMf dépend de la convention de signe adoptée dans vos cours.
Continuez. JED.
bonsoir et merci de votre reponse.
je comprends votre demarche mais seulement au niveau de Mf = 12500*x -7500*x^2 je ne pas compris l'apparution des 7500.
De plus votre symbole ^ signifie t-il division?
voici ce que je propose pour [AB].
en procedant ce que vous avez fait; dans cette intervalle il ya seulement Rc qui est appliquée.
par consequent en regardand de droite a gauche les actions, on aura: Mf= Rc(L-x).
qu'en pensez vous?
Bonsoir,
Le signe ^ est le carré.
La poutre porte l'axe Ax.
Soit une section S dans la poutre.
AS = x
Quelles sont les forces à gauche de S ?
La réaction RA = 12500 N
Un morceau de la charge répartie (p = 15000 N/m) de longueur x soit 15000x. On peut la remplacer
par une charge localisée 15000x appliquée à x/2 de A et de S.
Donc Mf = 12500*x -15000x*(x/2) ...........Continuez. JED.
Bonjour,
merci pour la reponse convaincante.
voici ce que je propose pour le reste de l'exercice:
pour l'intervalle [B;C].
je trouve M(x)= 7500-12500X.
3) M(x)max ? comme M(x) = 12500*x -15000x*(x/2) ;si x=1 alors M(x)max =5000N.m
De la même facon sur [B;C] ; M(x)max= 7500N.m.
c) Conclusion.
aidez moi avec vos critiques mais surtout votre proposition de resolution.
Que Dieu benisse  Bonjour,
Bonjour,
merci pour la reponse convaincante.
voici ce que je propose pour le reste de l'exercice[sup]Bonjour,
merci pour la reponse convaincante.
voici ce que je propose pour le reste de l'exercice:
pour l'intervalle [B;C].
je trouve M(x)= 7500-12500X.
3) M(x)max ? comme M(x) = 12500*x -15000x*(x/2) ;si x=1 alors M(x)max =5000N.m
De la même facon sur [B;C] ; M(x)max= 7500N.m.
c) Conclusion.
aidez moi avec vos critiques mais surtout votre proposition de resolution.
Que Dieu benisse Bonjour,
merci pour la reponse convaincante.
voici ce que je propose pour le reste de l'exercice[sup]Bonjour,
merci pour la reponse convaincante.
voici ce que je propose pour le reste de l'exercice:
pour l'intervalle [B;C].
je trouve M(x)= 7500-12500X.
3) M(x)max ? comme M(x) = 12500*x -15000x*(x/2) ;si x=1 alors M(x)max =5000N.m
De la même facon sur [B;C] ; M(x)max= 7500N.m.
c) Conclusion. ????
aidez moi avec vos critiques mais surtout votre proposition de resolution.
Que Dieu benisse!
Salut oswald,
La Rdm n'est pas une matière bien compliquée, à condition d'avoir bien compris les notions de base :
* PFS
* Torseur de cohésion
* Etc
J'avais essayé d'expliquer les méthodes de base à un membre sur des exemples simples (le rose correspondait à un effort réparti).
Je te conseille de lire ça très attentivement car cela va t'aider très fortement à trouver ton exo par toi-même, avec le soutien de JED bien évidemment 
![]() Résistance Des Matériaux ; ingénieur
Résistance Des Matériaux ; ingénieur
Bonjour et merci pour votre reponse.
j'ai aussi li votre indication mais j'aimerais que M. Jeg verifie ma proposition de reponse pour l'intervalle [A;B] et celle du reste.
Merci
Salut,
J'ai fait un peu ça à l'arrache j'espère ne pas avoir fait de fautes d'inattention :
1. Calcul des réactions aux appuis :
Par application du PFS (équation de la Rés /x et équation de Mt en A /z), je trouve :
et
Vérification :
2. Distribution du moment fléchissant :
on balaye la poutre de droite à gauche au niveau d'une section d'abscisse x, par l'application de la définition du torseur de cohésion, on fait :
* "+ ce qui est à droite de la section"
* "- ce qui est à gauche"
x dans l'intervalle [BC] :
x dans l'intervalle [AB] :
3. Moment fléchissant maximal :
Tu as deux méthodes :
soit l'étude de la fonction sur chaque intervalle
soit une astuce :
* pour x dans [BC], l'effort tranchant est positif donc Mfz est croissante sur l'intervalle. Hors en x = 2L, Mfz = 0
d'où un minimum en x = a.
En espérant que cela t'aidera 
Bonsoir et merci pour votre reponse.
apres avoir repris l'exercice, je comprend maintenant surtout avec votre reponse convaincante.
svp et la conclusion a tirer?
sur l'autre troncon, je trouve :
en derivant Mfz dans la meme intervalle; on trouve Ty =12500-7500x donc Ty est grand si x=1. alors Mfz=5000N.m
Remarque: dans votre message precedent du dernier; je pense que par inatention. vous avez mis l'expression de Ra en lieu et place de Rc.
Je t'en prie  .
.
En même temps, tu es tombé sur quelqu'un qui aime la Rdm ^^.
Le seul soucis est d'avoir le courage d'écrire les formules sur le forum au propre, et j'avoue que c'est parfois ce qui me décourage à intervenir.
Bonne soirée, à bientôt.


