Inscription / Connexion Nouveau Sujet
Exercice de Mécanique
Voici l'énoncé de l'exercice que je dois résoudre . Pour l'instant je bloque sur la question 1e/ le " En déduire " et sur la seconde partie de la question 2 a/ "en déduire la norme de la réaction normale du plan "Une masse m est lancée depuis le bas d'un plan incliné avec une vitesse initiale . On note a l'angle entre le plan incliné et l'horizontale.
1/ Etude du mouvement sans frottement :
Dans un premier temps, on suppose qu'il n'y a pas de frottement.
1a/ Faire un bilan des forces qui s'exercent sur la masse.
1b/ A partir de la 2ème loi de Newton, déterminer les expressions de l'accélération de la masse et de la réaction normale du plan incliné.
1c/ En déduire l'équation horaire x(t) du mouvement de la masse.
1d/ A quelle instant t0 la masse s'arrête-t-elle ?
1e/ En déduire que la hauteur maximale atteinte par la masse est h=V0²/2g Faire l'application numérique.
2/ Etude du mouvement avec frottement :
On suppose maintenant que le contact entre la masse et le plan est caractérisé par un coefficient de frottement solide µ=0,3.
2a/ Faire un nouveau bilan des forces qui s'exercent sur la masse à un instant t quelconque et en déduire la norme de la réaction normale du plan.
2b/ A partir de la 2ème loi de Newton, déterminer les expressions de la réaction normale et de l'accélération en fonction de m, g, et de la force de frottement solide T.
2c/ Rappeler la condition de glissement de la masse. En déduire .
2d/ Déterminer l'équation horaire x(t) du mouvement de la masse.
2e/ Quelle est la nouvelle expression de t0 ?
2f/ En déduire que la nouvelle hauteur maximum est h=v0²/(2G(1+µ/tan(a)))
2g/ Calculer h pour A=10° et A=30°.
2h/ Démontrer que le mobile reste alors en équilibre si avec l'angle limite que vous exprimerez en fonction de µ. Quel est le mouvement de la masse après son arrêt ?
3/ On se place dans le cas =10° et m=1kg. Après l'arrêt de la masse à la hauteur h, on veut la faire monter le plan incliné en exerçant une force constante.
3a/ Quelle est la valeur minimale F0 à donner à la norme de F dans le cas où l'on pousse la masse parallèlement au plan incliné ?
3b/ Quelle est la valeur minimale F1 à donner à la norme de F dans le cas où l'on pousse la masse horizontalement ?
MERCI D'AVANCE & BONNE JOURNEE 
Bonsoir ElenaG,
cet exercice n'est franchement pas difficile, surtout la premiere question qui est du niveau de terminale. Je suis donc etonne que tu ne saches pas la faire. Enfin bon...
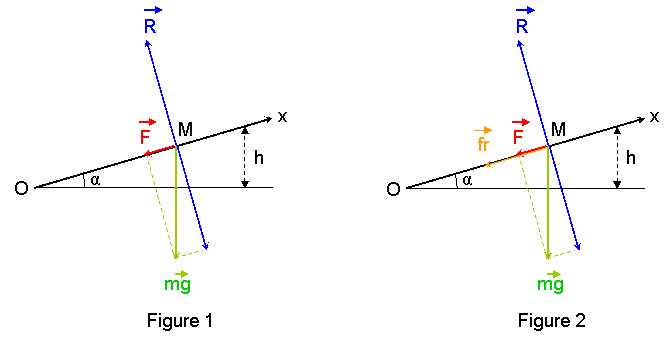
Regarde les figures ci-dessous, la premiere correspondant a la situation sans frottement, la seconde avec le frottement.
Plutot que de repondre question, je vais plutot faire une approche globale de l'exercice. L'examen des deux figures montre que dans chacun des deux cas le mobile M est soumis a des forces constantes en direction, sens et module. Donc le mouvement de M est uniformement varie, et meme uniformement retarde car les forces agissent en sens contraire du mouvement. De plus ce mouvement est unidirectionnel, uniquement sur l'axe Ox. Si on appelle a la valeur absolue de l'acceleration selon Ox (celle-ci est negative comme dit ci-dessus), on peut tout de suite ecrire les lois horaires du mouvement, archi-connues :
x(t) = -(1/2).a.t2 + V0.t, en supposant qu'a l'instant initial on est au point O de la rampe, et dx/dt = -at + V0.
La suite ne pose pas de probleme : la vitesse dx/dt s'annule au temps t0 = V0/a et en reportant dans x(t) j'obtiens l'expresion de xmax : xmax = V02/(2a). On en deduit la hauteur h atteinte par M lorsqu'il s'arrete : h = xmax.sin
= V02.sin/(2a). Vu ?
Question 1, pas de frottement :
Le poids mg (fleche verte) se projette sur l'axe Ox selon F = mg.sin, et sur l'axe 
a Ox selon la reaction R = mg.cos. Le mouvement se faisant sur Ox, la 2ieme loi de Newton donne R = mg.cos et a = F/m = g.sin.
Les relations etablies ci-dessus donnent : t0 = V0/(g.sin), xmax = V02/(2g.sin) et donc h = V02/(2g).
Question 2, frottement solide :
1ere chose a faire : reviser la definition du coefficient de frottement 
. Le frottement engendre une force fr opposee au mouvement et dont l'intensite est, par definition, fr = .R, R etant la reaction normale au plan (attention : cette relation n'est pas vectorielle puisque fr et R sont orthogonales : c'est uniquement une relation entre modules).
Le raisonnement precedent s'applique encore ici, avec fr = .mg.cos ; la resultante des forces appliquees a M est F' = F + fr = ma', ce qui donne une nouvelle expression de la norme de l'acceleration : a' = g(sin + .cos).
On en tire t'0 = V0/g(sin + .cos), x'max = V02/2g(sin + .cos) et h' = V02.sin/2g(sin + .cos) = V02/2g(1 + /tan).
Alors, ou etait la difficulte la-dedans ?
J'arrete ici car a) il est tard, et b) la question 2h et incomprehensible (il y manque au moins 2 mots).
A bientot, Prbebo.
Annuler
connectez vous