Inscription / Connexion Nouveau Sujet
Exercice de méca du solide
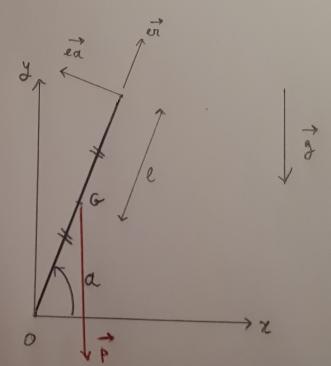
Bonjour à tous, je suis sur un exo étudiant une tige de longueur 2l, droite à l'état initiale, qu'on déséquilibre et qui s'écrase sur le sol
(cf pièce jointe)
Son moment d'inertie est J = 4/3 m l^2
Hypothèse : 0 frottements
On applique le TMC et après calcul on trouve :
a'' + 3g/4l cos a = 0 avec a, angle avec le sol
Cependant, si j'applique le théorème du centre de masse à G :
m aG = P + R
avec
OG = l ur
vG = la' ua
aG = -la'^2 ur +la'' ua
avec ur et ua vecteurs unitaires de la base polaire
en projetant sur ua on trouve
a'' + g/l cos a =0
Ainsi je trouve une équa diff différente que par le tmc... Pourquoi ??? Merci de vos réponses !
Bonjour
Impossible de t'aider sans un schéma précisant ce que tu appelles "a" et précisant les orientations des angles...
Un peut étonné tout de même que tu obtiennes une accélération angulaire négative...
Choisir comme sens positif de rotation le sens opposé à celui du mouvement ne peut que compliquer la situation en rendant plus délicate la gestion des signes mais bon : ce choix est peut-être imposé par l'énoncé...
Je suis d'accord avec ton résultat obtenu à partir du moment cinétique. Utiliser le théorème du centre de masse n'est pas possible directement car il faut tenir compte de la réaction du sol dont les deux composantes sont inconnues. Ce théorème permet justement, une fois connue l'expression de l'accélération, de déterminer les deux composantes de la réaction.
Si tu veux une méthode alternative pour obtenir l'expression de l'accélération, tu peux raisonner sur la conservation de l'énergie mécanique. La réaction du sol ne va pas intervenir dans le calcul dans la mesure où cette force ne travaille pas. Il suffit d'écrire :
Ok donc mon erreur a été de considérer que R était uniquement radiale ! (ce qui parait le plus intuitif pourtant ?)
Reste à calculer R en coordonnées cartésienne
Si je projette le TCM
selon x : ml(-a'^2 sin a + a'' sin a) = Rx
selon y : ml(-a'^2 sin a + a'' cos a) = Rx - mg
Il faut encore trouver a' ^2 :
on prend l'équa diff, on multiplie membre à membre par a' et on intégre
on a donc 1/2 a'^2 + 3g/4l sin a = c
avec c = 3g/4l (à t=0, a= pi/2 et a'=0)
il reste à réinjecter pour trouver a' et a'w !!!
Mais je ne saisis toujours pas bien pourquoi R a une composante selon ea?
Mais je ne saisis toujours pas bien pourquoi R a une composante selon ea?
S'il n'en était pas ainsi, le théorème du centre d'inertie, tel que tu l'as utilisé dans ton premier message, conduirait au même résultat que le théorème du moment cinétique.
La tige étant assimilée à un solide indéformable, il n'y a aucune raison pour que la réaction du sol soit colinéaire à
Ok merci c'est plus clair! une dernière question : tu dis que
La réaction du sol ne va pas intervenir dans le calcul dans la mesure où cette force ne travaille pas
Comment justifie tu cela ?
Ok merci c'est plus clair! une dernière question : tu dis que
La réaction du sol ne va pas intervenir dans le calcul dans la mesure où cette force ne travaille pas
Comment justifie tu cela ?