Inscription / Connexion Nouveau Sujet
Exercice de cinématique
Bonsoir à tous,
Je rencontre actuellement quelques difficultés à la résolution d'un exercice de cinématique, qui est le suivant:
" Une abeille, assimilable à un point mobile M, se déplace sur un arc de parabole (l'unité de longueur est le mètre) entre les instants tA=0 et T=2π/ω
Sur une figure est représenté arc de parabole, et l'équation de la parabole (Que j'ai déterminé):
y=-x2+x
"L'abeille part de A au temps tA=0, passe en C à l'instant tC= et arrive en B à l'instant tB=
. Son vecteur position, à chaque instant, est donné dans le repère cartésien par :
= 2α[1+cos(ωt)].
+αsin (ωt).
où α et ω sont des constantes positives.
On posera dans la suite: θ(t)=ωt, v0 =2αω et a0 =2αω2"
Les coordonnées de A, B et C sont respectivement A(4,0), B(0,0) et C(2,1)
On me demande de montrer que le mouvement de l'abeille est périodique et de déterminer sa période.
Faut-il faire: (t+T) ?
Comme le cosinus et sinus sont 2
-périodique alors la période est de 2 ?
De plus on me demande de déterminer l'équation de la trajectoire. Or je ne comprend pas trop... Faut-il prendre le problème normalement comme un tir parabolique ?
Bonsoir, La période de sin(
t) et cos(t) est T !
L'énoncé pose une difficulté : si tu poses :
= 2α[1+cos(ωt)].
+αsin (ωt).
,
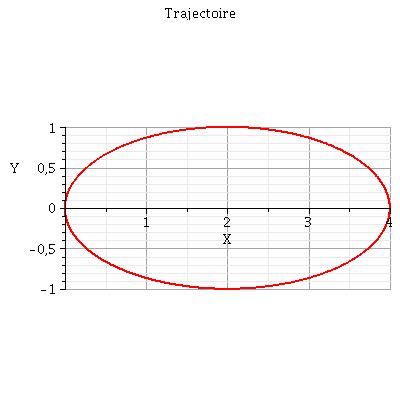
la trajectoire du point M n'est pas un arc de parabole. Voici en dessous ce que j'obtiens en ayant posé arbitrairement 
=1. Cela est cohérent avec les coordonnées des points A, B et C...
Je ne vois pas du tout le rapport avec un mouvement parabolique.
As-tu étudié les propriétés des ellipses ?
Remarque complémentaire :
Avec =1, l'équation de la trajectoire elliptique que j'ai tracée au dessus s'écrit :
Tu n'aurais pas par hasard "oublié" le carré de y2 dans l'équation que tu as écrite au début de ton message ?
Bonsoir,
On a seulement vue les ellipses dans les portraits de phase...
Le début de l'énoncé nous indique que l'abeille se déplace sur un arc de parabole et on a eu, comme figure joint avec le problème, l'arc supérieur de l'ellipse... Donc je pensais que l'abeille suivait un mouvement parabolique, vue que la figure s'agissait d'une chronophotographie...
Je ne comprend pas trop l'ellipse, pourquoi une ellipse ?
D'ailleurs que représente ? C'est homogène à des mètres en faisant l'analyse dimensionnelle.
est un paramètre d'échelle qui ici vaut 1m.
Pas question de faire ici un cours de math sur les ellipses ! disons simplement que, dans un repère (O',X,Y) où O' est le centre de symétrie de l'ellipse, les axes O'X et O'Y étant les deux axes de symétrie de l'ellipse, l'équation cartésienne de l'ellipse s'écrit :
ici, si tu exprimer sin(
) en fonction de y et cos() en fonction de x, la relation : conduit à :
Par identification : le centre de l'ellipse est O'(2m,0), le demi grand axe vaut a = 2m et le demi petit axe vaut b = 1m.
Pour le vecteur OM, veuillez m'excuser, j'ai oublié le carré sur le sinus ...
Je voulais notamment poser une dernière question, on me demande d'évaluer "" à l'aide de la figure donnée, qui n'est autre que la partie supérieur de votre ellipse que vous m'avez envoyé. Et donc vous m'avez dit qu'en choisissant arbitrairement =1 on retrouvais bien les coordonnées de A, B et C. Graphiquement comment fait-on ?
Annuler
connectez vous