Inscription / Connexion Nouveau Sujet
Exercice d'annale: théorème de thévenin (demande correction)
Bonjour à tous, voici petit exercice d'annales dont j'aimerais une correction en vue d'un examen:
(attachement 1: Circuit de l'énoncé)
- QUESTIONS :
1°) Théorème de Thévenin
a) Déterminer le courant i qui passe entre les points A et B en utilisant le théorème de Thévenin
b) AN: e1=4V, e2= 5V, R1= 50 , R2=200
, R2=200 , R3=50
, R3=50 , R4=100
, R4=100
- Alors, j'ai trouvé:
1°)Théorème de Thévenin
a) ETH=UAB à vide, je nomme i2 le courant de la maille toute à gauche et i3 le courant de la maille toute à droite
Eth=R2i2-R3i3+e2<=> ETH= R2e1/(R1+R2)-e3+e2 car i2=e1/(R1+R2) et i3=e3 (ça, j'en suis pas sûr)
RTH= R1//R2 = R1R2/(R1+R2)
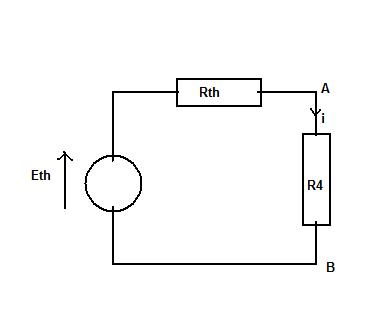
On a donc le circuit suivant:
(attachement 2: modèle de thévenin: je ne suis pas bien sûr du sens de ETH)
Avec ETH-RTHi-R4i=0 donc i=ETH/(RTH+R4)
b) AN: ETH=6.2V ; RTH=40 ; i= 44.2mA
; i= 44.2mA
Est-ce correct ?
Merci d'avance 
C'est peut-être pas très lisible, voici l'énoncé agrandi:
Bonjour,
Je suis d'accord avec les résultats suivants : valeurs littérales de ETH et RTH ainsi que valeur numérique de RTH
Je n'ai pas pu vérifier les valeurs numériques de ETH ni de i car tu n'as pas posté la valeur numérique de e3
Attention : tu ne peux pas écrire que i3 = e3 ; une intensité ne peut être égale à une tension. Ce que tu peux écrire c'est que la différence de potentiel UBC = e3 (à la condition que R3 ne soit pas nulle).

Oops, effectivement, e3=2V
Et, ça ne serait pas plûtot R3i3=e3 ?
L'exercice n'est pas terminé:
2°)Théorème de Millman
a)En supposant Vc=0V et en appliquant le théorème de millman, determiner les potentiels en chaque point du circuit.
b)En déduire une nouvelle fois i ainsi que les courants dans les autres branches du circuit.
c)AN.
Et là, je sèche:
a) Vc=(Vb/R3)/(1/R3) <=> Vc=Vb <=> Vb=0
C'est comme ça ?
Le théorème de Millman a été très peu abordé en cours et je ne sais pas ce qu'il en est quand les branches ne contiennent aucune résistance, entre C et F par exemple (division par zéro... ???) :/
Le potentiel du point C est pris pour l'origine des potentiels VC = 0 V
Tu en déduis immédiatement :
VF = VB
VD
VE
Le théorème de Millman est donc utile pour déterminer le potentiel VA du point A puisque tu connais les trois potentiels VE, VB et VD
Connaissant VA, tu en déduis à nouveau UAB = VA - VB
d'où i dans R4

Désolé, mais j'ai beaucoup de mal à comprendre ce théorème...
Je ne vois pas comment la formule peut être appliquée dans une branche sans résistance ( celle qui contient F: division par zéro ???) ni ce qu'il en est pour des courants sortant du noeud (valeur négative ?)...
Par exemple, Vb:
Vb=(Vf/0+Va/R4-Vc/R3)/(1/0+1/R4-1/R3) ???
:S
Donc euh..
Vb=(Va/R4)/(1/R4-1/R3)
d'où Vb=(VaR3)/(R3-R4)
Mais, on ne connait pas encore Va...
Je t'ai donné la marche à suivre le 30 à 16 h 10
En effet on ne connaît pas VA puisque c'est ce à quoi va servir le théorème de Millman

Oui, c'est la marche que j'essaye de suivre, seulement, je n'arrive pas à m'en sortir: je ne fais qu'exprimer, comme au dessus, Vb, Vd et Ve en fonction de Va (avec, qui plus est, des résultats improbables, du genre Ve=Va et Vd=Va)...
Forcément, quelque chose m'échappe... mais quoi ?
*voici ce que j'obtiens:
Vb==(VaR3)/(R3-R4) (vu au dessus...)
Ve=(Va/R1)/(1/R1)=Va, puisque je pars du principe qu'il n'y a pas de résistance entre E et D...
Vd=(Va/R2)/(1/R2)=Va, idem...
C'est assez frustrant...
VC = 0 V
VB = e3
VD = e2
VE = e2 + e1
Il ne manque plus qu'un seul potentiel : celui de A
C'est le moment d'appliquer le théorème de Millman.
Et tu retrouveras, bien sûr, les résultats que tu as déjà trouvés.

Ah mais oui !
Vb=Ubc puisque Ubc=Vb-Vc et Vc=0 !
Merci beaucoup !!! =)
Hum, avec le recul (et l'exam qui se profile...) j'ai de gros doutes qui me viennent:
Dans la première partie de l'exo, avais-je bien le droit d'attribuer un courant à toute une maille ? (j'ai dis que i2 était dans la maille de droite et i3 dans la maille de droite)
Mais, comment aurais-je pu faire autrement ?
J'ai pas compris comment tu as fait pour trouvez :
VD = e2
VE = e2 + e1
, j'ai essayé en appliquant la formule de millman :
Vd = (e2 + Va / R2 - e1 ) / ( 1/ R2)



