Bonsoir :
Si j'ai bien compris :
J'appelle l'angle entre la verticale et la tige, la vitesse angulaire de la tige à l'instant où l'action de la barre fixe s'annule, la tige n'étant ensuite soumise qu'à son poids... Pour une valeur de donnée,  Il faut trouver la valeur de pour que la tige se retrouve à la verticale lorsqu'elle touche le sol ... Ai-je bien compris ?
Quelle est la hauteur de la barre au-dessus du sol ?
A priori, on peut se sortir d'affaire en appliquant  la relation fondamentale de la dynamique et en appliquant le théorème du moment cinétique dans le référentiel barycentrique...
La modélisation sera tout de même extrêmement grossière : dans la pratique : le gymnaste se "groupe" de façon à fortement diminuer son moment d'inertie par rapport à l'axe de rotation passant par son centre d'inertie G. Il en résulte une forte augmentation de sa vitesse angulaire mesurée dans le repère barycentrique. Augmentation qui ne sera pas prise en compte ici puisque le gymnaste est assimilé à une tige indéformable...

Bonsoir, merci pour votre réponse.

Alors oui il faut trouver la bonne vitesse angulaire afin que la barre se retrouve à la vertical au sol.
La hauteur de la barre fixe nous a pas été donné, je pense que l'on peut nous même choisir cette valeur.

Qu'entendez-vous par un référentiel barycentrique? Il s agit du référentiel du centre de la tige modelisant le gymnaste?

Bonsoir, excusez-moi pour ma réponse plus que tardive.

Nous nous sommes penchées sur la résolution physique de ce problème.
Nous nous sommes demandées quelle devait être la vitesse initiale du gymnaste afin qu'il puisse faire un tour complet. Nous avons considéré l'énergie mécanique constante (pas de frottement). Ainsi nous avons considéré que l'énergie cinétique initiale (Ec) se transformait en énergie potentielle (Ep). On a considéré l'Ec = 0 en haut.
Nous avons fixé la taille du gymnaste à 2,2m (bras levés) et sa masse à 70kg
On a donc écris Ec=Ep pour en déduire vo, vo =2gh = 8.8m.s^-1
Est-ce correcte jusque là?

Nous voulions aussi appliquer la 2ème loi de newton afin de trouver les conditions sur laquelle la tension ne s'annule pas . Est-ce utile?
Pourriez-vous nous aider à trouver l'équation de la trajectoire?

cordialement

Peux-tu scanner ton schéma ? J'y verrai plus clair concernant tes notations.

Bonjour,

Pour la vitesse initiale, il s'agissait de la vitesse initiale du gymnaste enfin qu'il puisse faire un tour complet.  Il nous faudrait l'équation du mouvement de révolution autour de la barre fixe (avant qu'il la lâche) enfin de modéliser son mouvement sur un logiciel type sage.

L'equation que je vous demandais est celle de da trajectoire lorsqu'il lâche la barre.

Cordialement

Bonjour,
J'assimile le gymnaste à une tige de masse m et de Longueur L. Tant qu'il reste accroché à la barre , je considère qu'il tourne autour d'un axe horizontal, perpendiculaire au plan de figure et passant par B. Sa position initiale,d'indice 1 sur le schéma, correspond à une position verticale (pieds en B1) avec une vitesse initiale négligeable. Le moment d'inertie de la tige par rapport à l'axe de rotation est : . La position correspondant au lâché de la barre est la position d'indice 0 sur le schéma. Elle correspond à une inclinaison de l'angle    par rapport à la verticale, à une vitesse angulaire    et à une énergie cinétique   . Entre ces deux positions, la diminution d'altitude du centre de gravité est :   . Le théorème de l'énergie cinétique conduit à :


Soit :



Pour la suite, j'ai déjà indiqué la méthode : le point G décrit une trajectoire parabolique ; la tige tournant à la vitesse angulaire constante dans le repère barycentrique comme déjà expliqué... La position d'indice 2 est une position quelconque. J'ai schématisé la position finale (indice 3) par une position verticale, les pieds touchant le sol. Évidemment, dans ce cas, le gymnaste risque de tomber vers l'avant. On peut améliorer le modèle en considérant que les pieds touchent le sol lorsque le gymnaste est un peu incliné vers l'arrière (d'une vingtaine de degrés peut-être ???).
Remarques : la  figure n'est évidemment pas à l'échelle ! La date t = 0 correspond à l'instant où le gymnaste lâche la barre.

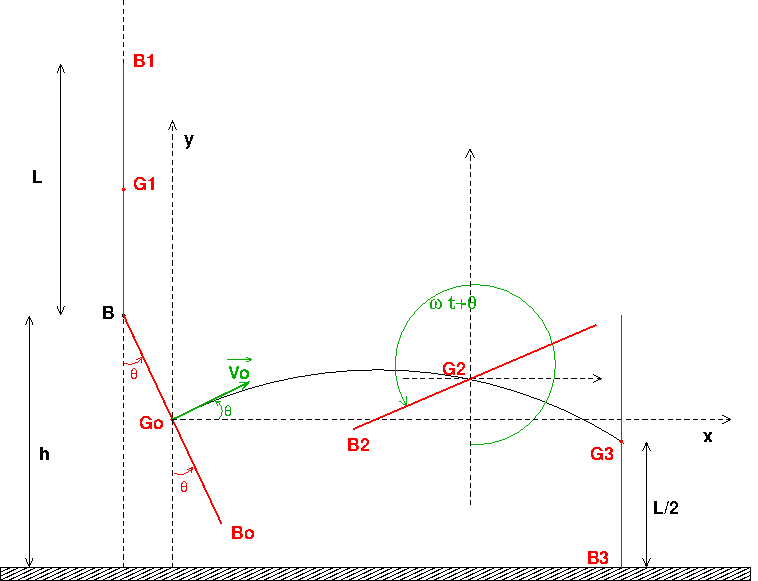
Je viens de terminer la simulation en écrivant que la durée nécessaire pour passer de la position initiale à la position finale est aussi la durée pour tourner de l'angle (2-).
Cela confirme mon message du  24-02-16 à 17:46 sur le nécessité d'augmenter la vitesse de rotation mesuré dans le repère barycentrique en diminuant le moment d'inertie au cours du mouvement. Si  le gymnaste ne se "groupe" pas pour augmenter sa vitesse de rotation, il n'a pas le temps d'effectuer la rotation de (2-) avant de toucher le sol.
Il te sera tout de même possible de déterminer la valeur minimale de pour que la rotation soit possible.

Bonjour,

nous avons reussi à modéliser notre animation sur python. Seul elle ne plait pas au prof car on a avant tout développer le côté informatique sans se servir de la physique.

Nous devons tout refaire. Savez-vous comment on peut trouver les équations du pendule simple en coordonnées cartésiennes car on les a qu'en coordonnées polaires et pour coder ce n'est vraiment pas pratique

cordialement

Bonjour,