Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Etude du mouvement d'un point oscillant

Posté par
amage 22-05-20 à 13:25

Bonjour !
J'ai rencontré des difficultés avec l'exercice suivant et j'aimerais que vous m'apportiez votre aide.
Exercice : Soit un triangle OO'B en O, d'hypoténuse O'B. Ce triangle tourne dans le sens positif autour de Oz suivant la loi = wt. Simultanément, le point M oscille le long de l'hypoténuse, de part et d'autre d'une position d'équilibre; l'élongation de M,est comptée positivement de O' vers B. On considère le repère fixe R = (O, i, j, k) et le repère mobile R' = (O', i', j', k') lié au triangle tel que k' = - e, er et e  sont les vecteurs de la base cylindrique définie à partir de M.
Étude cinématique (on travailleras dans la base R')
1) Déterminer directement les vecteurs vitesses et accélération absolues du point M
2) Déterminer les vecteurs vitesses relative et d'entrainement du point M
3) Déterminer les vecteurs accélérations relative, d'entrainement et de coriolis  du point M
4) Vérifier les lois de composition des vitesses et d'accélération.
Merci déjà pour l'attention accordée à mon post

Posté par
amagere : Etude du mouvement d'un point oscillant 22-05-20 à 13:29

Pour mon travail, j'ai bloqué dès la première question avec la détermination de l'expression du vecteur OM; en effet, j'ai décomposé en OO' + O'M pour O'M, j'ai posé O'M = xi' mais je n'arrive pas, même en utilisant le triangle rectangle OO'M à déterminer OO'. Mais ayant l'expression de OM dans R, je pense véritablement pouvoir continuer sans problèmes.
Merci d'avance.

Posté par
vanoisere : Etude du mouvement d'un point oscillant 22-05-20 à 14:07

Bonjour
L'énoncé est-il accompagné d'un schéma ? Si oui tu peux le scanner et le poster ici ; sinon, tu peux poster le schéma que tu as fait.

Posté par
amagere : Etude du mouvement d'un point oscillant 22-05-20 à 16:33

Ci-joint le schéma :

Etude du mouvement d\'un point oscillant

Posté par
vanoisere : Etude du mouvement d'un point oscillant 22-05-20 à 16:55

Si cela peut t'aider, essaie de faire une figure simplifiée avec comme plan de figure celui contenant le triangle (O,O',B). Tu verras alors que le vecteur unitaire \overrightarrow{i'} s'exprime simplement en fonction de \overrightarrow{e_{r}} , de \overrightarrow{k} et de l'angle . Pour obtenir les coordonnées absolues, il suffit alors simplement d'exprimer le vecteur \overrightarrow{e_{r}} en fonction de \overrightarrow{i} et \overrightarrow{j}.

Posté par
amagere : Etude du mouvement d'un point oscillant 22-05-20 à 17:27

vanoise @ 22-05-2020 à 16:55

Si cela peut t'aider, essaie de faire une figure simplifiée avec comme plan de figure celui contenant le triangle (O,O',B). Tu verras alors que le vecteur unitaire \overrightarrow{i'} s'exprime simplement en fonction de \overrightarrow{e_{r}} , de \overrightarrow{k} et de l'angle . Pour obtenir les coordonnées absolues, il suffit alors simplement d'exprimer le vecteur \overrightarrow{e_{r}} en fonction de \overrightarrow{i} et \overrightarrow{j}.
S'il vous plait j'ai du mal à connaitre où se situent exactement er et e sur le schéma; pouvez vous me donner de indications là dessus ?
Aussi, je n'arrive toujours pas à comprendre comment déterminer les composantes de OM suivant ces vecteurs.

Posté par
vanoisere : Etude du mouvement d'un point oscillant 22-05-20 à 18:10

\vec {e_r} est un vecteur unitaire colinéaire à \vec{OB} comme en base cylindrique classique. Le vecteur \vec e_\varphi qui ici devrait logiquement être noté \vec e_\theta est un vecteur orthogonal à \vec {e_r} dans le plan (Oxy). Il est donc ici perpendiculaire  au plan de figure et dirigé vers l'arrière.
Il y a maintenant un problème dans l'énoncé. Tel que tu l'as copié cet énoncé demande de poser : \overrightarrow{k'}=-\overrightarrow{e_{\varphi}} alors que la figure indique : \overrightarrow{j'}=\overrightarrow{e_{\varphi}}.
Que faut-il croire ?
J'ai préféré me fier à la figure et pas à l'énoncé mais ce n'est peut-être pas ce qui est attendu de ton professeur...  Je complète le trièdre direct en ajoutant le vecteur \overrightarrow{k'} . Cela donne, dans le plan contenant le triangle (O,O',B) la figure ci-dessous.

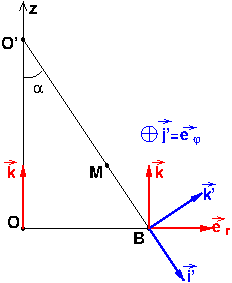
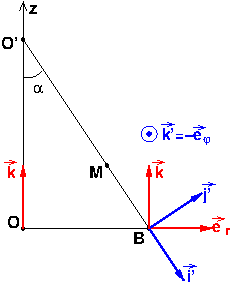
Etude du mouvement d\'un point oscillant

Posté par
vanoisere : Etude du mouvement d'un point oscillant 22-05-20 à 23:03

Je reviens sur le désaccord entre l'énoncé et le schéma évoqué dans mon message précédent. On peut aussi imaginer qu'il n'y a pas d'erreur d'énoncé : on a bien : \overrightarrow{k'}=-\overrightarrow{e_{\varphi}} et alors : il y a simplement une erreur de perspective dans le tracé du vecteur \vec{j'} à partir du point O'. Cela donne le schéma ci-dessous. Le vecteur k' est alors perpendiculaire au plan de figure et orienté vers l'avant de celle-ci.
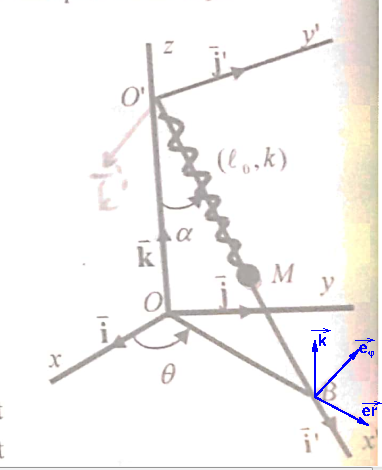
Je te conseille de vérifier ton énoncé. S'il comporte bien l'égalité : \overrightarrow{k'}=-\overrightarrow{e_{\varphi}} il serait sans doute plus prudent de considérer l'énoncé correct avec simplement un schéma en 3D pas très clair. Je te postes également le schéma que tu as scanné en y ajoutant les vecteurs \overrightarrow{e_{r}} et \overrightarrow{e_{\varphi}}.

Etude du mouvement d\'un point oscillant

Etude du mouvement d\'un point oscillant

Posté par
amagere : Etude du mouvement d'un point oscillant 23-05-20 à 02:57

Bonjour !
Merci pour toutes vos explications grâce auxquelles, j'ai pu mieux comprendre l'énoncé. Avant toute chose, j'aimerais signaler une erreur et je m'en excuse de ma part dans la première phrase de l'énoncé; c'est plutôt : "Soit un triangle rectangleOO'B en O, d'hypoténuse O'B."
Ceci étant, je pense, sur la base du plan (xoy) avec la présence de , qu'il s'agit d'une petite coquille et que par conséquent, l'on devrais également considérer e à la place de e dans l'optique  également d'utiliser les notations de la base cylindrique classique. Quant à vos observations sur l'orientation de j', je pense également, qu'il serait judicieux de considérer une erreur de perspective dans le tracé du vecteur j'.
Pour ce qui est de k' = -e, c'est bien ce que suggère l'énoncé comme vous pouvez le constater ici :

Posté par
amagere : Etude du mouvement d'un point oscillant 23-05-20 à 03:01

En image,

Etude du mouvement d\'un point oscillant

Posté par
vanoisere : Etude du mouvement d'un point oscillant 23-05-20 à 10:49

Merci pour ces précisions. Il faut donc conserver les notations de l'énoncé et les schémas de mon message du  22-05-20 à 23:03 en oubliant le schéma d'hier 18h10. Pour l'étude cinématique, mon message du  22-05-20 à 16:55 reste d'actualité.

Posté par
amagere : Etude du mouvement d'un point oscillant 23-05-20 à 15:28

vanoise @ 23-05-2020 à 10:49

Merci pour ces précisions. Il faut donc conserver les notations de l'énoncé et les schémas de mon message du  22-05-20 à 23:03 en oubliant le schéma d'hier 18h10. Pour l'étude cinématique, mon message du  22-05-20 à 16:55 reste d'actualité.

c'est moi qui vous remercie.
S'il vous plait, en ce qui concerne l'expression du vecteur OM, en particulier de ses coordonnées absolues, j'éprouve toujours des difficultés à les obtenir.

Posté par
amagere : Etude du mouvement d'un point oscillant 23-05-20 à 15:32

Je pense qu'il convient de poser :
OM = rer + zk

Posté par
vanoisere : Etude du mouvement d'un point oscillant 23-05-20 à 15:58

N'ayant pas l'énoncé intégral du problème, difficile de t'indiquer la méthode la plus rapide et efficace. Je pense tout de même qu'il s'agit d'étudier les oscillations de M le long de la tige O'B. La suggestion de ton premier message me parait plus prometteuse car elle va permettre ensuite facilement de faire intervenir les propriétés élastiques du ressort :
\\ \overrightarrow{OM}=\overrightarrow{OO'}+\overrightarrow{O'M}=\overrightarrow{OO'}+l_{(t)}.\overrightarrow{i'}

Le vecteur unitaire \overrightarrow{i'} s'exprime simplement en fonction de \overrightarrow{k}, \overrightarrow{e_{r}} et . Facile alors de dériver par rapport au temps pour obtenir la vitesse absolue de M puis son accélération absolue. Restera alors à exprimer ces deux vecteurs dans la base \left(\overrightarrow{i'},\overrightarrow{j'},\overrightarrow{k'}\right).

Posté par
amagere : Etude du mouvement d'un point oscillant 23-05-20 à 16:49

Veuillez trouver ci-joint l'intégralité de l'exercice :
Quand à OO' est-ce possible de poser : |OO'| = r par exemple ?

** image supprimée => l'énoncé doit être entière recopié**

Posté par
vanoisere : Etude du mouvement d'un point oscillant 23-05-20 à 18:19

Si tu veux mais cela importe peu ; Pour la suite, ce sont les vitesses et les accélérations qui importent et dériver par rapport au temps un vecteur constant donne le vecteur nul.

Posté par
amagere : Etude du mouvement d'un point oscillant 23-05-20 à 18:47

D'accord compris !
Je tiens à vous remercier grandement pour votre aide.

Posté par
amagere : Etude du mouvement d'un point oscillant 27-05-20 à 10:33

amage @ 23-05-2020 à 16:49

Veuillez trouver ci-joint l'intégralité de l'exercice :
Quand à OO' est-ce possible de poser : |OO'| = r par exemple ?

** image supprimée => l'énoncé doit être entière recopié**

Bonjour !
J'ai déterminé la vitesse absolue et j'aimerais vous faire part de mon résultat enfin d'avoir votre avis.
OM = OO' + O'M = zk + x'i'
\frac{dOM}{dt} = \dot{z} + \frac{dx'i'}{dt}
or, \frac{di'}{dt} = \dot{\theta }k\wedge i' d'où : \frac{di'}{dt} = \dot{\theta }(sin\alpha )k
et donc, V_{a}(M) = \dot{z}k + \dot{x}i' - x'\dot{\theta }(sin\alpha )k or, OO'B est rectangle en O donc OO' = z = cste et = cste et finalement,
V_{a}(M) = \dot{x}i' - x'\dot{\theta }(sin\alpha )k.
Merci d'avance !

Posté par
vanoisere : Etude du mouvement d'un point oscillant 27-05-20 à 10:58

Il s'agit peut-être juste d'une étourderie dans l'utilisation de l'éditeur d'équation.

\overrightarrow{i'}=\sin\left(\alpha\right).\overrightarrow{e_{r}}-\cos\left(\alpha\right).\overrightarrow{k}

\frac{d\overrightarrow{i'}}{dt}=\omega.\overrightarrow{k}\wedge\overrightarrow{i'}=\omega.\sin\left(\alpha\right).\left(\overrightarrow{k}\wedge\overrightarrow{e_{r}}\right)=\omega.\sin\left(\alpha\right).\overrightarrow{e_{\varphi}}=-\omega.\sin\left(\alpha\right).\overrightarrow{k'}

Dans ton résultat final, il suffit donc de remplacer \overrightarrow{k} par \overrightarrow{k'} :

\overrightarrow{V_{a}(M)}=\dot{x'}.\overrightarrow{i'}-\omega.\sin\left(\alpha\right).x'.\overrightarrow{k'}

Posté par
amagere : Etude du mouvement d'un point oscillant 27-05-20 à 12:58

vanoise @ 27-05-2020 à 10:58

Il s'agit peut-être juste d'une étourderie dans l'utilisation de l'éditeur d'équation.

\overrightarrow{i'}=\sin\left(\alpha\right).\overrightarrow{e_{r}}-\cos\left(\alpha\right).\overrightarrow{k}

\frac{d\overrightarrow{i'}}{dt}=\omega.\overrightarrow{k}\wedge\overrightarrow{i'}=\omega.\sin\left(\alpha\right).\left(\overrightarrow{k}\wedge\overrightarrow{e_{r}}\right)=\omega.\sin\left(\alpha\right).\overrightarrow{e_{\varphi}}=-\omega.\sin\left(\alpha\right).\overrightarrow{k'}

Dans ton résultat final, il suffit donc de remplacer \overrightarrow{k} par \overrightarrow{k'} :

\overrightarrow{V_{a}(M)}=\dot{x'}.\overrightarrow{i'}-\omega.\sin\left(\alpha\right).x'.\overrightarrow{k'}

Oui tout à fait c'est bien k' que j'ai obtenu sur papiers. Merci beaucoup pour votre aide


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !