Inscription / Connexion Nouveau Sujet
Etude de la myopie
Bonjour!
J'ai commencé un exercice d'optique géométrique, cependant j' ai quelques difficultées à le réaliser.
Voici l'énoncé: Sachant que l' on teste la vue d' une personne myope
sur un banc optique doté de sa lanterne à la graduation 0 et d'un support à lentille , la personne place son oeil de l'autre côté de la lentille au point S.
Ce point S est à 10,00 cm du centre optique O de la lentille.
Le support est doté d'une lentille de vergence -0,500 dioptries.
L'objet sera noté AB, A étant sur l'axe optique.
L'observateur voit net pour une distance entre l'objet et la lentille comprise entre 2 m et 5,1 cm
1)Déterminer les positions des images par rapport à la lentille
J'ai trouvé f' car V=1/f' donc f'=-2
après j'ai calculé pour OA=5,1 cm
Avec la relation de conjuuaison de Descartes j'obtiens 5,2cm cependant j'obtiens 0 avec 2m ce qui me laisse penser qu'il y a une erreur de ma part
2)En déduire les positions du punctum remotum et proximum de l'oeil
Pp=5,2cm
Pr=? je ne vois pas comment l'on peut faire même s'il doit être d'une dizaine de cm normalement pour un oeil myope
3) Calculer l'amplitude dioptrique de l'oeil
J'ai besoin des valeurs de la question 2
Il y a d'autres questions mais déja j'aimerais avoir un epu d'aide sur celles_ci s'il vous plaît!
Merci beaucoup!
Bonjour
Juste quelques indications.
Attention aux unités. Écrire f'=-2 n'a pas de sens physique.
Pour la suite, l'oeil ne voit pas l'objet AB mais l'image A'B' de cet objet par la lentille puisque l'oeil regarde à travers la lentille . Il faut donc déterminer la position de A' quand A est 2m avant la lentille puis quand A est 5,1cm avant la lentille.
Merci beaucoup! oui effectivement, c'est vrai qu'il ne faut pas oublier les unités.
pour A à 5,1 cm je trouve avec la loi de conjuguaison de Descartes, 5,2cm.
Cependant avec 2m je trouve 0 n'est ce pas étrange?
Je me demande si tu ne commets pas d'erreur de signe...
Quand A est 2m avant la lentille, A' est 1m avant la lentille soit à 1,1m de S. Quand A est 5,1cm avant la lentille, A' est 5,0cm avant la lentille soit à 15cm de S.
Bonsoir
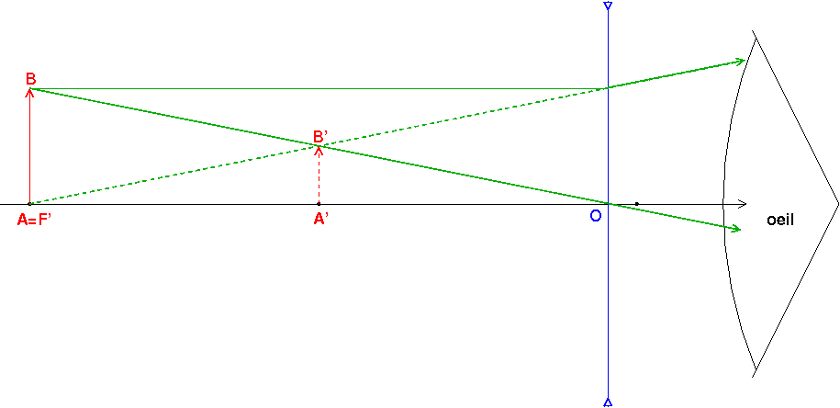
Je crois que tu as quelques difficultés avec les mesures algébriques. Je te présente le calcul et le schéma dans le cas où l'objet est 2m devant la lentille, le point A' étant ainsi confondu avec le point F'. Le schéma montre que l'image A'B' est virtuelle et située du même côté de la lentille que l'objet. L'œil “voit” donc A'B' en regardant à travers la lentille. La formule de conjugaison de Descartes s'écrit :
Ici :
Les données ne sont pas toutes fournies avec le même nombre de chiffres significatifs... J'ai considéré que la distance objet lentille est connue avec 2 chiffres significatifs et non un seul comme tu l'as écrit.