Inscription / Connexion Nouveau Sujet
Etude d'une mouvement circulaire
Bonjour,
Je viens de commencer des cours de mécanique, et je ne comprends rien aux différents systèmes de coordonnées. Voici un exercice que je n'arrive même pas à commencer :
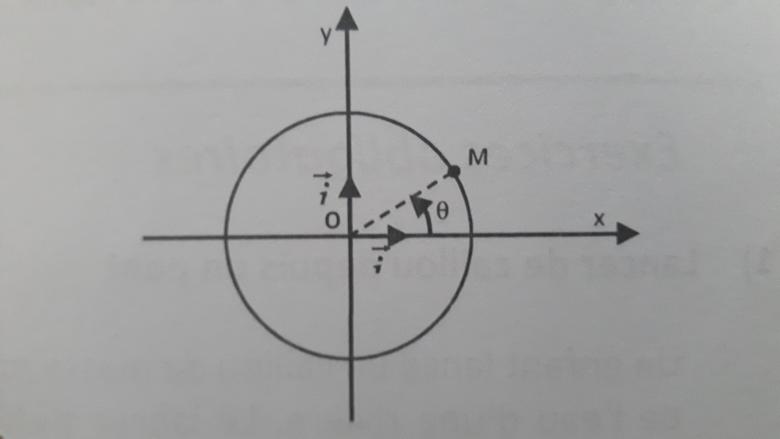
On considère un point mobile M animé d'un mouvement circulaire uniforme. Sa trajectoire décrit un cercle de centre O et de rayon R dans le repère orthonormé cartésien (O,  ,
,
 ) (voir figure ci-contre).
) (voir figure ci-contre).
1- Donner l'expression vectorielle de la position OM, de la vitesse v et de l'accélération a en utilisant les coordonnées cartésiennes, en fonction de R et 
2- Donner l'expression vectorielle de la position OM, de la vitesse v et de l'accélération a en utlisant les coordonnées polaires, en fonction de R et 
(Vecteur en gras)
Je n'arrive pas du tout à écrire ces expressions.
Merci d'avance pour votre aide.
AR2
En coordonnées cartésiennes.
En supposant Msur l'axe des x en t = 0 :
xM = R.cos(theta)
yM = R.sin(theta)
et theta = w.t (avec theta en rad, w la vitesse angulaire en rad/s et t en s)
-->
xM = R.cos(w.t)
yM = R.sin(w.t)
vect(OM) = R.cos(w.t) . vect(i) + R.sin(w.t) . vect(j)
en dérivant par rapport au temps :
vect(vM) = -wR.sin(w.t) . vect(i) + wR.cos(w.t) . vect(j)
en dérivant par rapport au temps :
vect(aM) = -w²R.cos(w.t) . vect(i) - w²R.sin(w.t) . vect(j)
-----
En coordonnées polaires.
Voir par exemple ici : ![]()
Sauf distraction. 


